目录
第一章 空间解析几何与向量代数
考点1: 空间直角坐标系
1.1 给定点M(x,y,z) 判定坐标点所在象限:
解题方法:
1. 根据 M(x,y) 找出平面直角坐标系象限。
2. 判断平面直角坐标系:
z>0:原象限。
z<0:原象限+4。
例如:
M(1,2,3): 象限 = 1;
M(1,2-3): 象限 = 5;
真题:
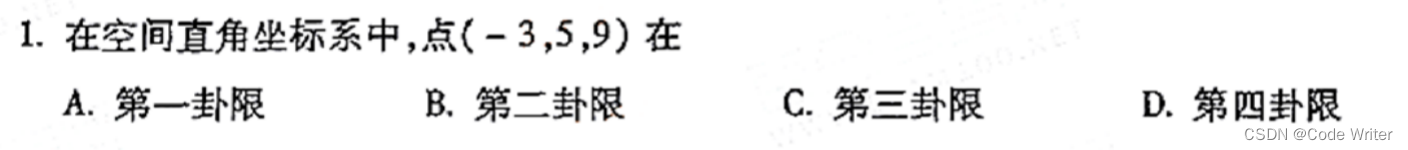
答案为:B、第二卦限(象限)
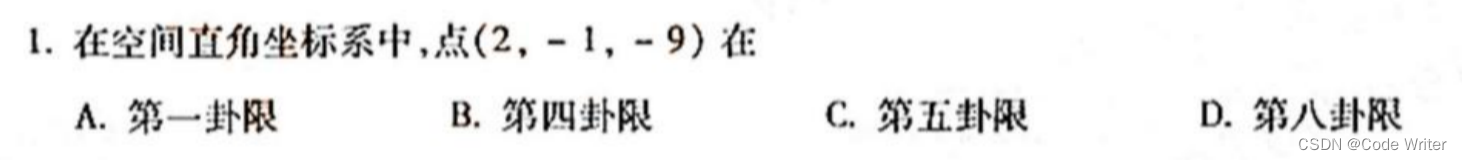
答案为:D、第八卦限
下图为平面直角坐标系的象限判定图:
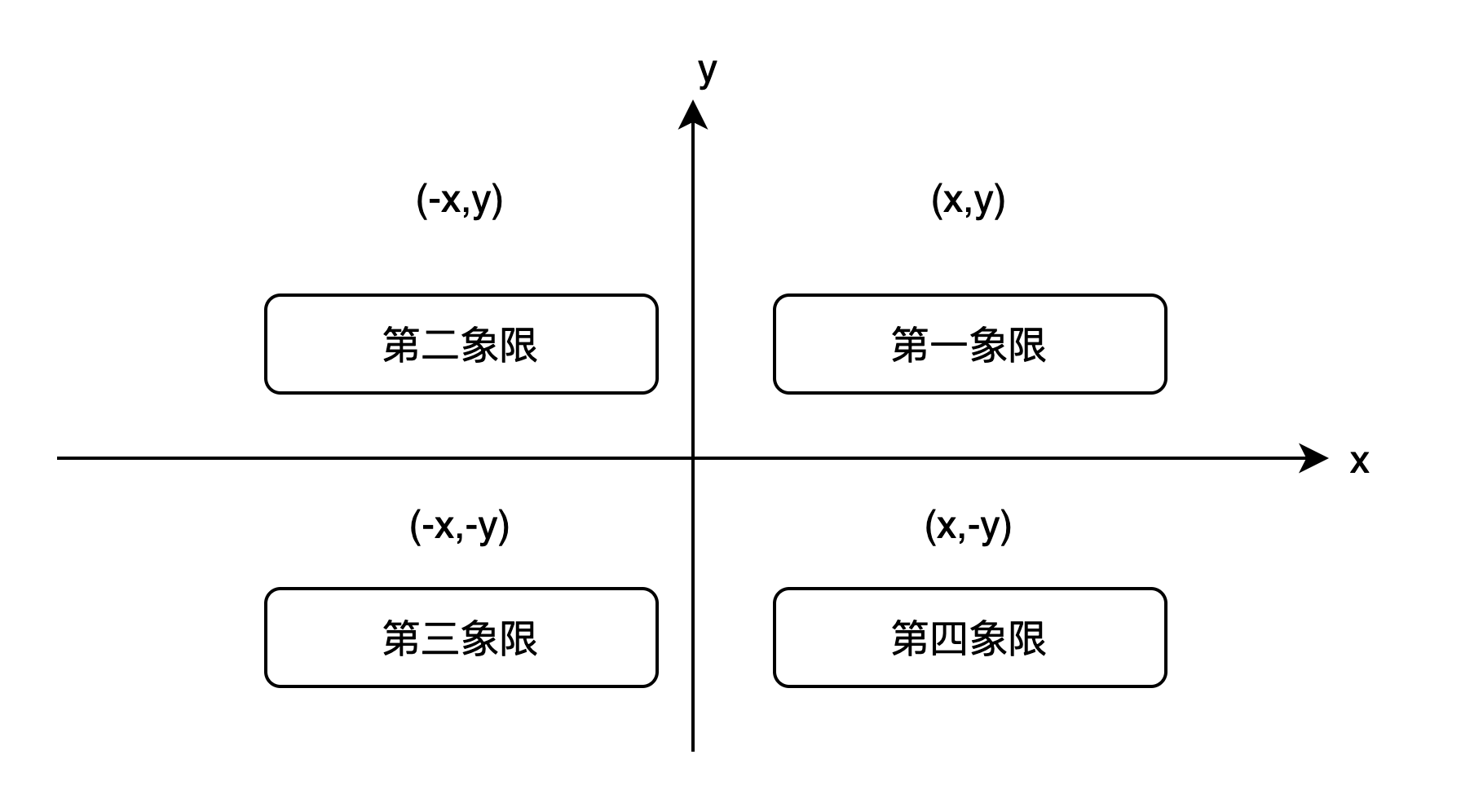
1.2 对称性质
关于原点对称:M(x,y,z) -> M(-x,-y,-z)
关于坐标轴对称:例如x轴对称:M(x,y,z) -> M(x,-y,-z)
关于坐标面对称:例如Oxy轴对称:M(x,y,z)->(x,y,-z)
真题:

答案:B

答案:A

答案:C
考点2: 向量代数
2.1 向量的取模运算
∣
α
∣
=
a
1
2
+
a
2
2
+
a
3
2
|\alpha|=\sqrt{a_1^2+a_2^2+a_3^2}
∣
α
∣
=
a
1
2
+
a
2
2
+
a
3
2
真题:

答案:
∣
α
∣
=
2
2
+
(
−
2
)
2
+
1
2
=
4
+
4
+
1
=
9
=
3
|\alpha|=\sqrt{2^2+(-2)^2+1^2} = \sqrt{4+4+1} = \sqrt{9}=3
∣
α
∣
=
2
2
+
(
−
2
)
2
+
1
2
=
4
+
4
+
1
=
9
=
3
2.2 向量的数量积
α
⋅
β
=
a
1
b
1
+
a
2
b
2
+
a
3
b
3
;
\alpha \cdot \beta = a_1b_1+a_2b_2+a_3b_3;
α
⋅
β
=
a
1
b
1
+
a
2
b
2
+
a
3
b
3
;
真题:
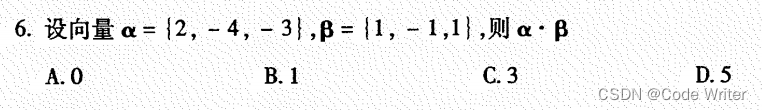
答案:
(
2
∗
1
)
+
(
−
4
∗
−
1
)
+
(
−
3
∗
1
)
=
2
+
4
−
3
=
3
(2*1)+(-4*-1)+(-3*1)=2+4-3=3
(
2
∗
1
)
+
(
−
4
∗
−
1
)
+
(
−
3
∗
1
)
=
2
+
4
−
3
=
3
答案:C
2.3 向量坐标运算
α
±
β
=
{
a
1
±
b
1
,
a
2
±
b
2
,
a
3
±
b
3
}
\alpha \pm \beta = \{a_1 \pm b_1,a_2 \pm b_2 ,a_3 \pm b_3 \}
α
±
β
=
{
a
1
±
b
1
,
a
2
±
b
2
,
a
3
±
b
3
}
;
λ
α
=
{
λ
a
1
,
λ
a
2
,
λ
a
3
}
\lambda \alpha = \{ \lambda a_1, \lambda a_2,\lambda a_3 \}
λ
α
=
{
λ
a
1
,
λ
a
2
,
λ
a
3
}
;
真题:混合运算:
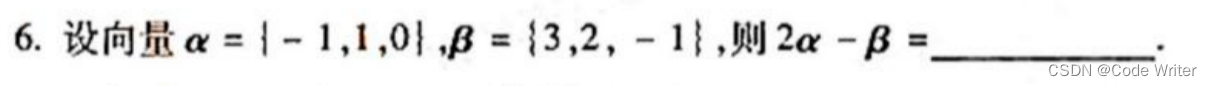
答案:
2
{
−
1
,
1
,
0
}
−
{
3
,
2
,
1
}
=
{
−
2
,
2
,
0
}
−
{
3
,
2
,
1
}
=
{
(
−
2
−
3
)
,
(
2
−
2
)
,
(
0
−
(
−
1
)
)
}
=
{
−
5
,
0
,
1
}
2\{-1,1,0\}-\{3,2,1\}=\{-2,2,0\}-\{3,2,1\}=\{(-2-3),(2-2),(0-(-1))\}=\{-5,0,1\}
2
{
−
1
,
1
,
0
}
−
{
3
,
2
,
1
}
=
{
−
2
,
2
,
0
}
−
{
3
,
2
,
1
}
=
{(
−
2
−
3
)
,
(
2
−
2
)
,
(
0
−
(
−
1
))}
=
{
−
5
,
0
,
1
}
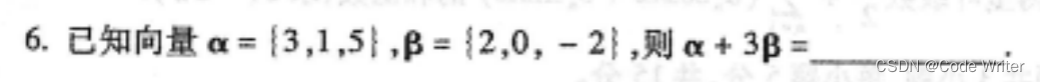
答案:{3,1,5}+2{2,0,-2}={3,1,5}+{6,0,-6} = {9,1,-1}
考点3: 平面方程
3.1 平面方程
点法式方程:
一般式方程:
- 点到直线垂直的平面方程
- 点与平面平行的平面方程
- 过3点的平面方程
- 两平面的夹角
- 点到平面的距离公式
3.2 两个平面的夹角
3.3 点到平面的距离
考点4: 直线方程
对称式方程:
一般式方程:
参数方程:
- 过两点的直线方程
- 平面与直线的夹角
- 两直线夹角
- 求方向向量