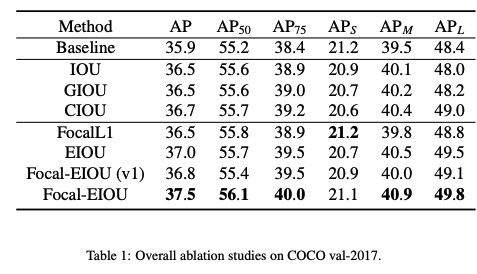
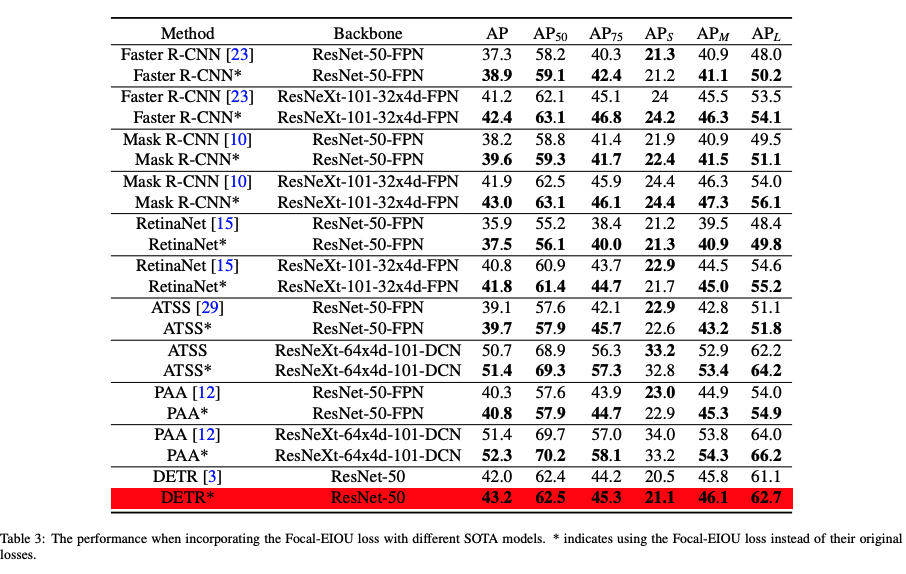
论文:
Focal and Efficient IOU Loss for Accurate Bounding Box Regression
贡献点:
- 总结了现有回归 loss 的问题:最重要的是没有直接优化需要优化的参数
- 提出了现有方法收敛速度较慢的问题,很多的低质量样本贡献了大部分的梯度,限制了框的回归
- 提出了 Focal-EIoU,平衡高质量样本和低质量样本对 loss 的贡献,也就是提升高质量(IoU 大)样本的贡献,抑制低质量(IoU 小)样本的贡献
一、背景
目标检测框的回归问题,主要有两种 loss 函数:
-
ln
l_n
l
n
-norm 函数
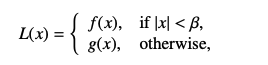
-
IoU-based 函数
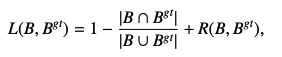
- IoU loss 的问题:当两个框不相交时,IoU loss 将无法更新,且无法反应两个框的距离远近,收敛速度很慢
- GIoU loss 的问题:使用惩罚项会让网络趋于选择更大的和 gt 有相交的 anchor,收敛速度很慢,当两框为包含关系时,退化为 IoU loss,收敛速度也很慢
- DIoU loss 的问题:考虑了中心点距离,但没考虑 anchor 的纵横比
-
CIoU loss 的问题:虽然考虑的纵横比的问题,但是通过其公式中的
vv
v
反映的纵横比的差异,而不是宽高分别与其置信度的真实差异,anchor 的长和宽不能同时增大或减小。
CIoU 的详细对比:
-
当两个框为等比例缩放的时候,
v=
0
v=0
v
=
0
,难以被优化 -
ww
w
和
hh
h
其中一个增大,另一个必然减小,无法同时增大或减小,抑制了模型的优化。因为
∂v
∂
w
=
−
h
w
.
∂
v
∂
h
\frac{\partial v}{\partial w} = – \frac{h}{w}.\frac{\partial v}{\partial h}
∂
w
∂
v
=
−
w
h
.
∂
h
∂
v
,而偏导又是正值,所以有这样的关系。 - 只关心两者比例,而非每个边对应的真实差距,容易导致不期望的优化方式。如图 1 所示,当 gt 框的长和宽都为 1 时,初始 anchor w=1,h=2.4。50 次迭代后,w=1.64,h=2.84,所以 CIoU 更期望提升两个框纵横比的相似性,而非真实的长和宽。

二、方法
2.1 EIoU Loss
EIoU Loss 定义如下:
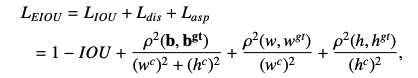
-
wc
w^c
w
c
和
hc
h^c
h
c
是最小包围框的宽和长 - EIoU loss 可以分为 3 部分:IoU loss + 距离 loss + 纵横比 loss
- EIoU loss 直接最小化 anchor 和 gt 的宽和高的差异,使得收敛速度更快,定位效果更好
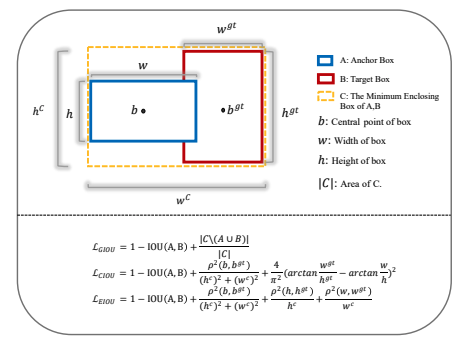
2.2 Focal EIoU Loss
在框回归问题中,高质量的 anchor 总是比低质量的 anchor 少很多,这也对训练过程有害无利。所以,需要研究如何让高质量的 anchor 起到更大的作用。
1、Focal L1 Loss
首先,损失函数的特性要求如下:
- 当回归的误差趋于 0 时,梯度的模值也会趋于 0
- 梯度的模值应该在小回归误差处快速上升,在大回归误差处逐步下降
- 需要有一些超参数来控制低质量 anchor 灵活性的抑制程度
- 梯度函数需要在 (0, 1] 之间,来平衡高质量和低质量 anchor
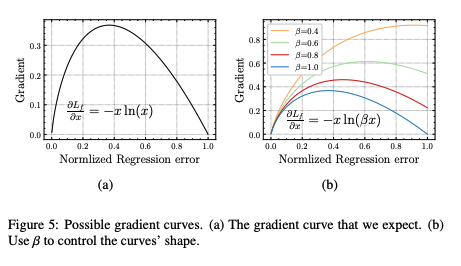
满足 1 和 2 条件的函数如图 5a 所示,当添加了一个超参数
β
\beta
β
时,如图 5b 所示,随着
β
\beta
β
的增大,虽然难样本的梯度模值会被很大程度的抑制,但高质量样本的梯度模值会降低,这并非期望的结果。
所以,又添加了一个参数
α
\alpha
α
,来将梯度模值归一化到 [0, 1],所以,梯度模值可以被写为:
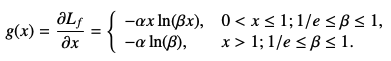
所以,得到能够对边界框进行回归监督的 Focal L1 Loss 如下:
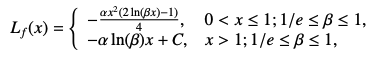
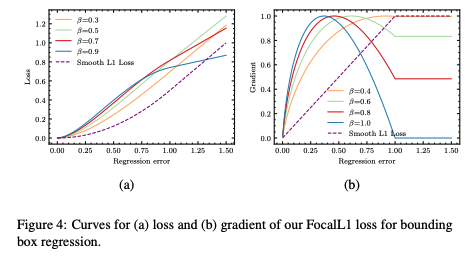
如图 4b 所示,Focal L1 Loss 可以提高 inliers 的梯度值,并根据
β
\beta
β
抑制 outliers 的梯度值:
-
β\beta
β
越大,则 inliers 会有小的回归误差,并且快速抑制 outliers 的梯度值
如图 4a 所示:
-
蓝色线是
β\beta
β
的最大值,随着回归误差的增大,蓝色线会先很快增大,然后稳定 -
橘色线是
β\beta
β
是在
β\beta
β
最小时,会快速增长,然后在 x=1 时达到峰值 -
经过消融实验,最后选择
β=
0.8
\beta=0.8
β
=
0.8
,即红线所示
2、Focal-EIoU Loss
为了让 EIoU Loss 更关注高质量样本,可以使用 EIoU loss 来代替上面公式中的 x,但效果不太好。所以作者就通过分析之后,提出了下面的最终形式:
L
F
o
c
a
l
−
E
I
o
U
=
I
o
U
γ
L
E
I
o
U
L_{Focal-EIoU}=IoU^{\gamma} L_{EIoU}
L
F
oc
a
l
−
E
I
o
U
=
I
o
U
γ
L
E
I
o
U
-
γ=
0.5
\gamma=0.5
γ
=
0.5
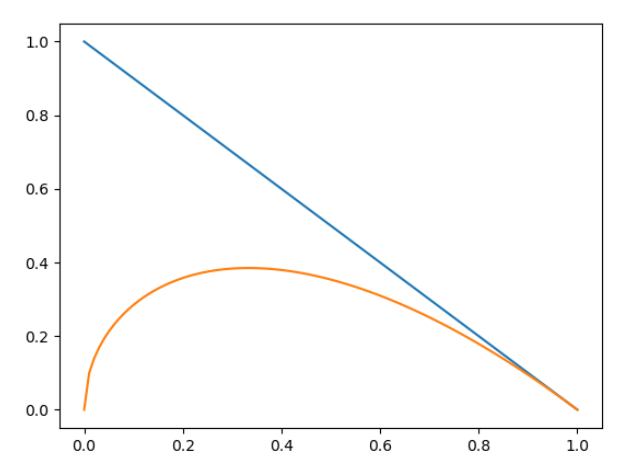
这里以 IoU loss 的形式来分析一下 Focal 形式的曲线(EIoU 曲线不太好画),蓝线为
(
1
−
I
o
U
)
(1-IoU)
(
1
−
I
o
U
)
曲线,橘色线为
I
o
U
0.5
(
1
−
I
o
U
)
IoU^{0.5}(1-IoU)
I
o
U
0.5
(
1
−
I
o
U
)
,所以在 IoU 小的时候(0-0.8),
I
o
U
0.5
(
1
−
I
o
U
)
IoU^{0.5}(1-IoU)
I
o
U
0.5
(
1
−
I
o
U
)
会被拉低,在 IoU 大的时候(0.8-1),
I
o
U
0.5
(
1
−
I
o
U
)
IoU^{0.5}(1-IoU)
I
o
U
0.5
(
1
−
I
o
U
)
基本保持不变。
从这个曲线可以看出,Focal-EIoU loss 能够通过降低难样本的 loss 来让网络更关注简单样本。
三、效果