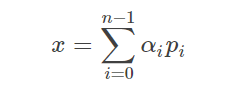

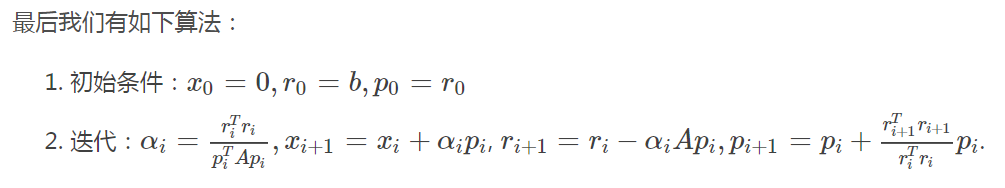
P的更新是根据施密特正交化原理,可以保证
![]()
,
![]()
的更新是根据
![]()
得到的。
因为
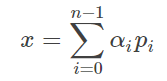
和
![]()
,所以
![]()
;又因为
![]()
,所以
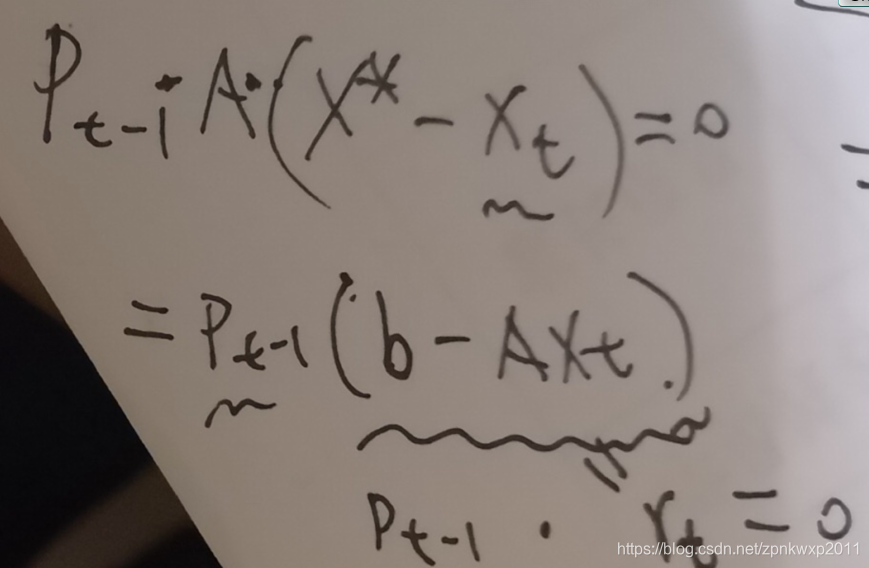
,同理有
![]()
。
几何意义是P(t-1)与《“P(t-1)这个方向和椭圆的贯穿线的中点“到椭圆的中心点〉是共轭正交关系,P(t-1)与残差是一般的正交关系。
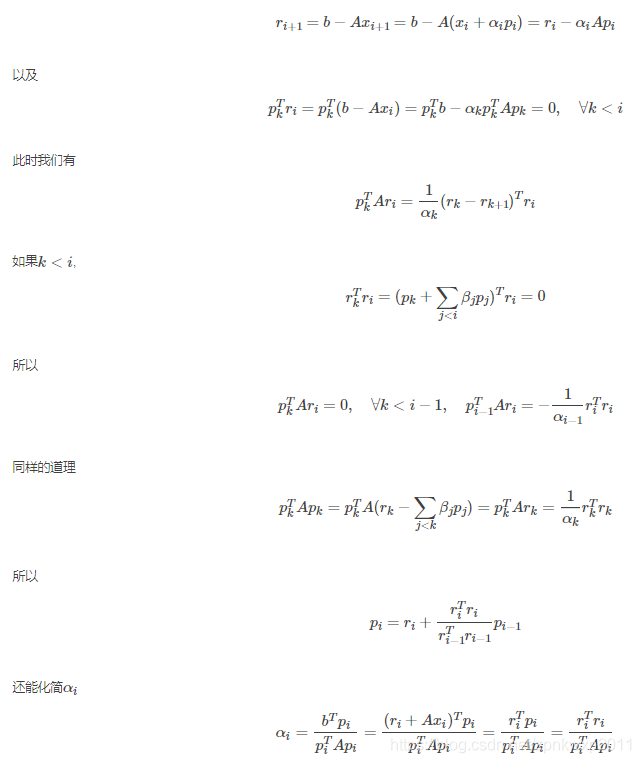
对上图的解释如下:
其中

表示只要i不等于k,ri乘以rk就是0,所以
![]()
;
因为
![]()
,所以
![]()
;
因为P的正交性,所以有
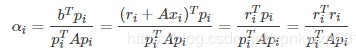
。