什么是机器学习
机器学习是人工智能的一个子集,目前已经发展出许多有用的方法,比如
支持向量机,回归,决策树,随机森林,强化方法,集成学习,深度学习
等,一定程度上可以帮助人们完成一些
数据预测,自动化,自动决策,最优化
等初步替代脑力的任务。
什么是神经网络
神经网络就是按照一定规则将多个神经元连接起来的网络。
神经网络有三种层:输入层负责接受信息比如一张猫的图片;输出层是计算机对这个输入信息的判断结果,它是不是猫;隐藏层就是对输入信息的传递和加工处理。
大数据、机器学习和数据挖掘的定义
大数据
被定义为“超出常用软件工具捕获,管理和处理能力”的数据集。
机器学习
关心的问题是如何构建计算机程序使用经验自动改进。
数据挖掘
是从数据中提取模式的特定算法的应用,在数据挖掘中,重点在于算法的
应用
,而不是算法的本身。
机器学习和数据挖掘的关系
数据挖掘是一个
过程
,在此过程中机器学习算法被用作提取数据集中的潜在有价值模式的
工具
。
大数据和深度学习的关系
深度学习
是一种模拟大脑的行为,可以从所学习对象的机制以及行为等很多相关联的方面进行学习,模仿类型行为以及思维。
深度学习对于⼤数据的发展有帮助。深度学习对于⼤数据技术开发的每⼀个阶段均有帮助,不管是数据的分析还是挖掘还是建模,只有深度学习,这些⼯作才会有可能⼀⼀得到实现。
深度学习转变了
解决问题的思维
。在深度学习的基础上,要求我们从开始到最后都要基于一个目标,为了优化那个最终目标去进行
处理数据
以及
将数据放到数据应用平台
上去,这就是
端到端(end to end)。
大数据的深度学习需要一个框架。将大数据通过深度分析变为现实,这就是深度学习和大数据的最直接关系。
机器学习的学习方式——监督学习、非监督学习、半监督学习
监督学习
:使⽤
已知正确答案
的⽰例来训练⽹络。已知数据和其⼀⼀对应的标签,训练⼀个预测模型,将输⼊数据映射到标签的过程。
常⻅应⽤场景:监督式学习的常⻅应⽤场景如
分类
问题和
回归
问题。
非监督学习
:数据并
不被特别标识
,适⽤于你具有数据集但⽆标签的情况。学习模型是为了
推断
出数据的⼀些内在结构。
常⻅应⽤场景:常⻅的应⽤场景包括
关联规则
的学习以及
聚类
等。
半监督学习下
:输⼊数据部分被标记,部分没有被标记,这种学习模型可以⽤来进⾏预测。
常⻅应⽤场景:应⽤场景包括
分类
和
回归
,算法包括⼀些对常⽤监督式学习算法的延伸,通过对已标记数据建模,在此基础上,对未标记数据进⾏预测。
分类算法
分类算法
和
回归算法
是对真实世界不同建模的⽅法。分类模型是认为模型的输出是
离散
的,例如⼤⾃然的⽣物被划分为不同的种类,是离散的。回归模型的输出是
连续
的,例如⼈的⾝⾼变化过程是⼀个连续过程,⽽不是离散的。
在实际建模过程时,采⽤分类模型还是回归模型,取决于你对任务(真实世界)的分析和理解。
– -常见的分类算法
Bayes ⻉叶斯分类法、Decision Tree决策树、SVM⽀持向量机、KNN K近邻、Logistic
Regression逻辑回归、Neural Network神经⽹络、Adaboosting。
逻辑回归
在广义线性模型家族里,如果是二项分布,就是逻辑回归。
– -逻辑回归的适用性
(1)⽤于
概率预测
。=⽐如根据模型进⽽预测在不同的⾃变量情况下,发⽣某病或某种情况的概率有多⼤。 (2)⽤于
分类
。实际上跟预测有些类似,也是根据模型,判断某⼈属于某病或属于某种情况的概率有多⼤,也就是看⼀下这个⼈有多⼤的可能性是属于某病。进⾏分类时,仅需要设定⼀个阈值即可,可能性⾼于阈值是⼀类,低于阈值是另⼀类。 (3)
寻找危险因素
。寻找某⼀疾病的危险因素等。 (4)仅能⽤于
线性问题
。只有当⽬标和特征是线性关系时,才能⽤逻辑回归。 (5)各特征之间不需要满⾜条件独⽴假设,但各个特征的贡献独⽴计算。
– -生成模型和判别模型的区别
生成模型
:由数据学习联合概率密度分布P(X,Y),然后求出条件概率分布P(Y|X)作为预测的模型,即⽣成模型:P(Y|X)= P(X,Y)/ P(X)(⻉叶斯概率)。典型的⽣成模型有朴素⻉叶斯,隐⻢尔科夫模型等。
举例
:利⽤⽣成模型是根据⼭⽺的特征⾸先学习出⼀个⼭⽺的模型,然后根据绵⽺的特征学习出⼀个绵⽺的模型,然后从这只⽺中提取特征,放 到⼭⽺模型中看概率是多少,在放到绵⽺模型中看概率是多少,哪个⼤就是哪个。
判别模型
:由数据直接学习决策函数Y=f(X)或者条件概率分布P(Y|X)作为预测的模型,即判别模型。典型的判别模型包括k近邻,感知级,决策树,⽀持向量机等。
举例
:要确定⼀个⽺是山羊还是绵⽺,⽤判别模型的⽅法是从历史数据中学习到模型,然后通过提取这只⽺的特征来预测出这只羊是山羊的概率,是绵⽺的概率。
逻辑回归是判别模型, 朴素贝叶斯是⽣成模型
,所以⽣成和判别的所有区别它们都有。
什么是代价函数
-为了得到训练逻辑回归模型的参数,需要⼀个代价函数,通过训练代价函数来得到参数。
-⽤于找到最优解的⽬的函数。
– -代价函数的原理
在回归问题中,通过代价函数来求解最优解,常⽤的是平⽅误差代价函数。
平方误差代价函数
的主要思想就是将实际数据给出的值与拟合出的线的对应值做差,求出拟合出的直线与实 际的差距。在实际应⽤中,为了避免因个别极端数据产⽣的影响,采⽤类似⽅差再取⼆分之⼀的⽅式来减⼩个别数据的影响。
以函数h(x)=A+Bx为例:
想要拟合函数图的离散点,我们需要尽可能找到最优的A和B来使这条直线更能代表所有数据。如何找到最优解呢,这就需要使⽤代价函数来求解,以平⽅误差代价函数为例,假设函数为h(x)=θx。
因此,引出代价函数:
最优解即为代价函数的最小值。
什么是损失函数
损失函数(Loss Function)⼜叫做误差函数,⽤来衡量算法的运⾏情况,估量模型的预测值与真实值的不⼀致程度,是⼀个⾮负实值函数,通常使⽤L( Y , f(x) )来表示。
损失函数越⼩,模型的鲁棒性就越好。损失函数是经验⻛险函数的核⼼部分,也是结构⻛险函数重要组成部分。
一个例子明白什么是梯度下降
假如最开始,我们在⼀座⼤⼭上的某处位置,因为到处都是陌⽣的,不知道下⼭的路,所以只能摸索着根据直觉,⾛⼀步算 ⼀步,在此过程中,每⾛到⼀个位置的时候,都会求解当前位置的梯度,沿着梯度的负⽅向,也就是当前最陡峭的位置向下⾛⼀步,然后继续求解当前位置梯度,向这⼀步所在位置沿着最陡峭最易下⼭的位置⾛⼀步。不断循环求梯度,就这样⼀步步地⾛下去,⼀直⾛到我们觉得已经到了⼭脚。当然这样⾛下去,有可能我们不能⾛到⼭脚,⽽是到了某⼀个局部的⼭势低处。 由此,从上⾯的解释可以看出,梯度下降不⼀定能够找到全局的最优解,有可能是⼀个 局部的最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就⼀定是全局最优解。
机器学习中为什么需要梯度下降
梯度下降是机器学习中常⻅
优化算法
之⼀,梯度下降法有以下⼏个作⽤:
(1)梯度下降是迭代法的⼀种,可以⽤于求解最⼩⼆乘问题。
(2)在求解机器学习算法的模型参数,即⽆约束优化问题时,主要有梯度下降法(Gradient Descent)和最⼩⼆乘法。
(3)在求解损失函数的最⼩值时,可以通过梯度下降法来⼀步步的迭代求解,得到最⼩化的损失函数和模型参数值。
(4)如果我们需要求解损失函数的最⼤值,可通过梯度上升法来迭代。梯度下降法和梯度上升法可相互转换。
(5)在机器学习中,梯度下降法主要有随机梯度下降法和批量梯度下降法。
梯度下降的核心思想
(1)初始化参数,随机选取取值范围内的任意数;
(2)迭代操作: a)计算当前梯度; b)修改新的变量; c)计算朝最陡的下坡⽅向⾛⼀步; d)判断是否需要终⽌,如否,返回a);
(3)得到全局最优解或者接近全局最优解。
如何对梯度下降法调优
(1)
算法迭代步长选择
。 在算法参数初始化时,有时根据经验将步⻓初始化为1。实际取值取决于数据样本。可以从⼤到⼩,多取⼀些值,分别运⾏算法 看迭代效果,如果损失函数在变⼩,则取值有效。如果取值⽆效,说明要增⼤步⻓。但步⻓太⼤,有时会导致迭代速度过快,错过最优解。步⻓太⼩,迭代 速度慢,算法运⾏时间⻓。
(2)
参数的初始值选择
。 初始值不同,获得的最⼩值也有可能不同,梯度下降有可能得到的是局部最⼩值。如果损失函数是凸函数,则⼀定是最优解。由 于有局部最优解的⻛险,需要多次⽤不同初始值运⾏算法,关键损失函数的最⼩值,选择损失函数最⼩化的初值。
(3)
标准化处理
。 由于样本不同,特征取值范围也不同,导致迭代速度慢。为了减少特征取值的影响,可对特征数据标准化,使新期望为0,新⽅差为1, 可节省算法运⾏时间。
线性判别分析(LDA)
线性判别分析(Linear Discriminant Analysis,LDA)是⼀种经典的降维⽅法。和主成分分析PCA不考虑样本类别输出的⽆监督降维技术不同,LDA是⼀种监督学习的降维技术,数据集的每个样本有类别输出。
LDA分类思想
- 多维空间中,数据处理分类问题较为复杂,LDA算法将多维空间中的数据投影到⼀条直线上,将d维数据转化成1维数据进⾏处理。
- 对于训练数据,设法将多维数据投影到⼀条直线上,同类数据的投影点尽可能接近,异类数据点尽可能远离。
- 对数据进⾏分类时,将其投影到同样的这条直线上,再根据投影点的位置来确定样本的类别。
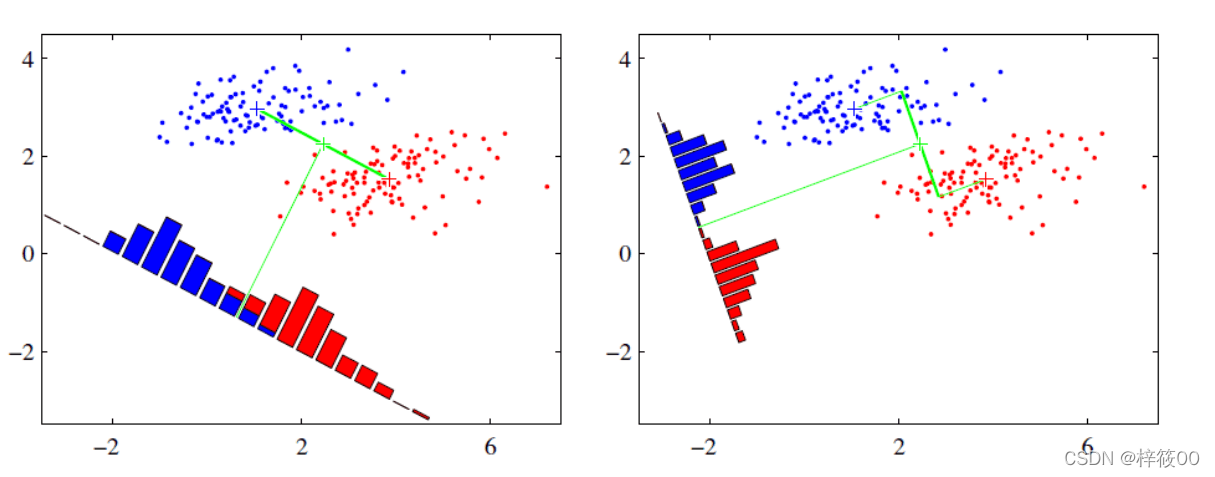
LDA思想图解
假设有红、蓝两类数据,这些数据特征均为⼆维,如下图所⽰。我们的⽬标是将这些数据投影到⼀维,让每⼀类相近的数据的投影点尽可能接近,不同类 别数据尽可能远,即图中红⾊和蓝⾊数据中⼼之间的距离尽可能⼤。
PCA思想总结
- PCA就是将⾼维的数据通过线性变换投影到低维空间上去。
- 投影思想:找出最能够代表原始数据的投影⽅法。被PCA降掉的那些维度只能是那些噪声或是冗余的数据。
- 去冗余:去除可以被其他向量代表的线性相关向量,这部分信息量是多余的。
- 去噪声,去除较⼩特征值对应的特征向量,特征值的⼤⼩反映了变换后在特征向量⽅向上变换的幅度,幅度越⼤,说明这个⽅向上的元素差异也越 ⼤,要保留。
- 对⾓化矩阵,寻找极⼤线性⽆关组,保留较⼤的特征值,去除较⼩特征值,组成⼀个投影矩阵,对原始样本矩阵进⾏投影,得到降维后的新样本矩 阵。
- 完成PCA的关键是——协⽅差矩阵。协⽅差矩阵,能同时表现不同维度间的相关性以及各个维度上的⽅差。协⽅差矩阵度量的是维度与维度之间的关 系,⽽⾮样本与样本之间。
- 之所以对⾓化,因为对⾓化之后⾮对⾓上的元素都是0,达到去噪声的⽬的。对⾓化后的协⽅差矩阵,对⾓线上较⼩的新⽅差对应的就是那些该去掉 的维度。所以我们只取那些含有较⼤能量(特征值)的维度,其余的就舍掉,即去冗余。
图解PCA核心思想
PCA可解决训练数据中存在数据
特征过多或特征累赘
的问题。核⼼思想是将m维特征映射到n维(n < m),这n维形成主元,是重构出来最能代表原始数据的正交特征。
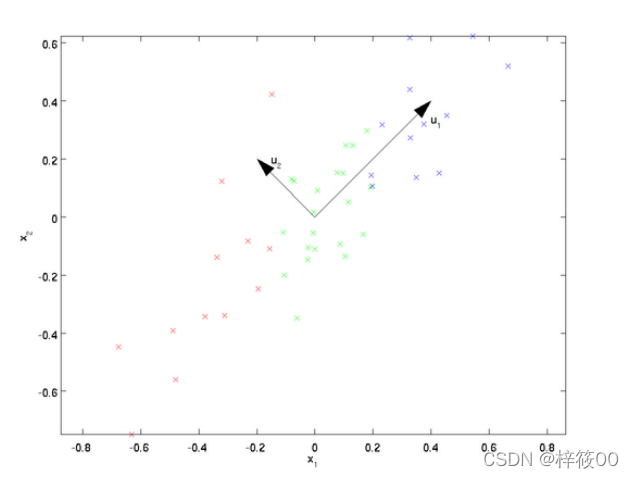
假设数据集是m个n维,如果 n = 2,需要降维到 n` = 1,现在想找到某⼀维度⽅向代表这两个维度的数据。下图有u1、u2两个向量⽅向,由于u1的样本点到这个直线的距离⾜够近;样本点在这个直线上的投影能尽可能的分开。所以u1可以更好代表原始数据集。
降维的必要性
- 多重共线性和预测变量之间相互关联。多重共线性会导致解空间的不稳定,从⽽可能导致结果的不连贯。
- ⾼维空间本⾝具有稀疏性。⼀维正态分布有68%的值落于正负标准差之间,⽽在⼗维空间上只有2%。
- 过多的变量,对查找规律造成冗余⿇烦。
- 仅在变量层⾯上分析可能会忽略变量之间的潜在联系。例如⼏个预测变量可能落⼊仅反映数据某⼀⽅⾯特征的⼀个组内。
降维的目的
- 减少预测变量的个数。
- 确保这些变量是相互独⽴的。
- 提供⼀个框架来解释结果。相关特征,特别是重要特征更能在数据中明确的显⽰出来;如果只有两维或者三维的话,更便于可视化展⽰。
- 数据在低维下更容易处理、更容易使⽤。
- 去除数据噪声。
- 降低算法运算开销。
