一、数据结构概述
1、数据结构与算法的重要性
算法是程序的灵魂,优秀的程序可以在海量数据计算的时候,依然保持高速计算。
一般来讲,程序使用了内存计算框架(比如Spark)和缓存技术(比如Redis)来优化程序,再深入思考一下,这些计算框架和缓存技术,它的核心功能就是数据结构与算法。 拿实际工作经历说,在Unix下开发服务器程序,功能是要支持上千万人同时在线,在上线前,进行测试都OK,可是上线后,服务器就撑不住了,公司的CTO对代码进行优化,再次上线,就坚如磐石。这是程序的灵魂——算法。
2、数据结构与算法的关系
数据(data)结构(structure)是一门研究组织数据方式的学科,有了编程语言也就有了数据结构,学好数据结构可以编写出更加漂亮,更加有效率的代码。
要学好数据结构就要多多考虑如何将生活中遇到的问题,用程序去解决。
程序 = 数据结构 + 算法
数据结构是算法的基础,换言之,想要学好算法,就要把数据结构学到位
3、实际编程中遇到的问题
封装好的API
Java代码:
public static void main(String[] args) { // write your code here String str = "hello,world!hello,view6view!"; String newStr = str.replaceAll("hello","你好"); System.out.println(newStr); }
问:试写出用单链表表示的字符串类以及字符串结点类的定义,并依次实现它的构造函数、以及计算长度、串赋值,判断两串相等、求子串、两串连接、求字串在串中位置等7个成员函数。
游戏逻辑设定
一个五子棋程序:
如何判断优秀的输赢,并可以完成存盘退出和继续上局的功能棋盘—>二维数组—>稀疏数组—>写入文件【存档功能】—>读取文件—>稀疏数组—>二维数组—>棋盘【接上局】
约瑟夫(Josephu)问题
Josephu问题为:设编号为1,2,3,….n的n个人围坐一圈,约定编号为K(1<=k<=n)的人从1开始报数,数到m的那个人出列,他的下一位又从1开始报数,数到m的那个人又出列,依次类推,知道所有人出列为止,由此产生一个出队编号的序列。
提示:用一个不带头节点的循环列表来处理Josephu问题:先构成一个由n个结点的单循环链表(单向循环列表),然后由k结点从1开始计数。计到m时,对应结点从链表中删除,然后再从被删除结点的下一个删除结点又开始从1开始技术,直到最后一个结点从链表中删除算法结束。
其它常见问题
修路问题 —> 最小生成树(数+ 普利姆算法)
最短路径问题 —> 图 + 弗洛伊德算法
汉诺塔问题 —> 分治算法
八皇后问题 —>回溯法
4、线性结构与非线性结构
线性结构
线性结构作为最常用的数据结构,其特点是
数据元素之间存在一对一
的线性关系。
线性结构有两种不同的存储结构,即
顺序存储结构
和
链式存储结构
。顺序存储结构的线性表称为顺序表,顺序表中的存储元素是连续的。
链式存储的线性表称为链表,链表中的存储元素不一定是连续的,元素节点中存放数据元素以及相邻元素的地址信息。
线性结构常见的有:数组、队列、链表和栈,后面我会相信讲解。
非线性结构
非线性结构包括:二维数组,多维数组,广义表,树结构,图结构
二、稀疏数组
1、基本介绍
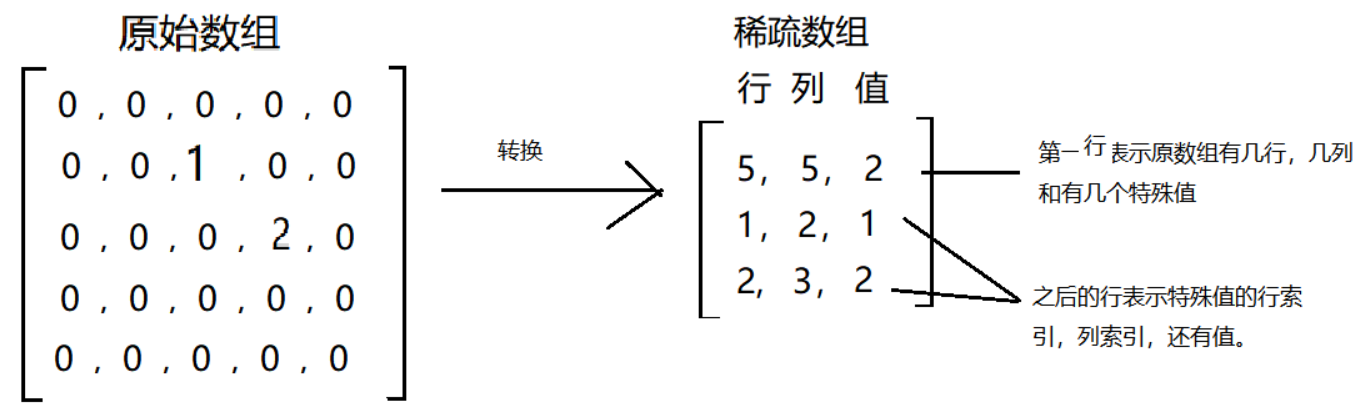
当一个数组中大部分元素为0,或者为同一个值的数组时,可以用稀疏数组来保存该数组。
2、稀疏数组的处理方法是
- 记录数组一共有几行几列,有多少个不同的值
- 把具有不同值的元素的行、列及值记录在一个小规模数组(稀疏数组)中,从而缩小程序的规模
3、稀疏数组转换思路的分析
二维数组转稀疏数组的思路
便利原始的二维数组,得到有效数据的个数sum
根据sum就可以创建稀疏数组
Integer sparseArr[][] = new Integer[sum+1][3]
将二维数组的有效数据存入到稀疏数组中
稀疏数组转原始的二维数组的思路
先读取稀疏数组的第一行,根据第一行的数据,创建原始的二维数组,比如
Integer[11][11] chessArr2
再读取稀疏数组后几行的数据,并赋值给原始的二维数组即可

4、代码实现
public class SparseArray { public static void main(String[] args) { // 创建一个11*11的二维数组 int cheseArray[][] = new int[11][11]; cheseArray[1][2] = 1; cheseArray[2][4] = 2; cheseArray[3][6] = 2; // 打印当前二维数组 for (int[] row: cheseArray){ for (int data: row){ System.out.printf("%d\t",data); } System.out.println(); } int sum = 0; for (int i = 0; i < 11; i ++){ for (int j = 0 ; j < 11; j ++ ){ if (cheseArray[i][j] != 0){ sum++; } } } System.out.println(sum); // 构建稀疏数组 int sparseArray[][] = new int[sum + 1][3]; sparseArray[0][0] = 11; sparseArray[0][1] = 11; sparseArray[0][2] = sum; // 将二维数组中不为0的元素放入稀疏数组中 int count = 0; for (int i = 0; i < 11; i ++){ for (int j = 0 ; j < 11; j ++ ){ if (cheseArray[i][j] != 0){ count++; sparseArray[count][0] = i; sparseArray[count][1] = j; sparseArray[count][2] = cheseArray[i][j]; } } } // 打印稀疏数组 for (int i = 0; i< sparseArray.length; i ++){ System.out.printf("%d\t%d\t%d\t\n",sparseArray[i][0],sparseArray[i][1],sparseArray[i][2]); } System.out.println(); // 再将稀疏数组转为二维数组 int cheseArray2[][] = new int[sparseArray[0][0]][sparseArray[0][1]]; for (int i = 1; i< sparseArray.length; i ++){ cheseArray2[sparseArray[i][0]][sparseArray[i][1]] = sparseArray[i][2]; } // 输出恢复后的二维数组 System.out.println(); for (int[] row: cheseArray2){ for (int data: row){ System.out.printf("%d\t",data); } System.out.println(); } } }
5、控制台输出结果
0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 3 11 11 3 1 2 1 2 4 2 3 6 2 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
三、队列
1、普通队列
应用场景
- 队列是一个有序列表,可以用
数组
或是
链表
实现- 遵循
先入先出
的原则。即:先存入队列的数据,要先取出。后存入的要后取出。
使用数组模拟队列示意图
- 队列本身也是有序列表,若使用数组的结构来存储队列的数据,则队列数组的声明如下图,其中MaxSize为队列的最大容量
- 因为队列的输出输入是分别从前后端来处理,因此需要两个变量
front和rear分别记录前后端的下标
,front会随着数据输出而改变,而rear会随着数据输入而改变
数组模拟队列实现
当我们将数据存入队列时称为”addQueue”,addQueue 的处理需要有两个步骤:思路分析
1) 将尾指针往后移:rear + 1 , 当 rear == front 【空】
2) 若尾指针 rear 小于队列的最大下标 MaxSize-1,则将数据存入 rear 所指的数组元素中,否则无法存入数据。 reatr == MaxSize – 1[队列满]
public class ArrayQueueDemo { public static void main(String[] args) { // 创建一个队列 ArrayQueue arrayQueue = new ArrayQueue(3); char key = ' '; // 接受用户输入 Scanner scanner = new Scanner(System.in); boolean loop = true; System.out.println("s(show):显示队列"); System.out.println("e(exit):退出程序"); System.out.println("a(add):添加数据到队列"); System.out.println("g(get):从队列取数据"); System.out.println("h(head):查看队列头的数据"); while (loop) { key = scanner.next().charAt(0); // 接收第一个字符 switch (key) { case 's': arrayQueue.showQueue(); break; case 'a': System.out.println("输入一个数:"); int value = scanner.nextInt(); arrayQueue.addQueue(value); break; case 'g': try { int res = arrayQueue.getQueue(); System.out.printf("取出的数据是%d\n", res); continue; } catch (RuntimeException e){ System.out.println(e.getMessage()); } break; case 'h': try { int res = arrayQueue.headQueue(); System.out.printf("队列头的数据是%d\n", res); } catch (RuntimeException e){ System.out.println(e.getMessage()); } break; case 'e': scanner.close(); loop = false; break; default: break; } } System.out.println("程序退出"); } } // 使用数组模拟队列 - 编写一个ArrayQueue类(非循环队列,只能使用一次) class ArrayQueue { private int maxSize; // 表示数组的最大容量 private int front; // 队列头 private int rear; // 队列尾 private int[] arr; // 该数据用于存放数据,模拟队列 // 创建队列的构造器 public ArrayQueue(int maxSize) { this.maxSize = maxSize; arr = new int[maxSize]; front = -1; // 队列头下标,取值的时候发生变动 rear = -1; // 队列尾下标,增加值的时候发生变动 } // 判断队列是否满 public boolean isFull() { // 例如最大容量为5,rear是指向队列尾部数据,所以rear为4(maxSize - 1)的时候就为满了 return rear == maxSize - 1; } // 判断队列是否为空 public boolean isEmpty() { // 因为不是循环队列,头尾不相连,所以rear == front 时队列就为空 return rear == front; } // 添加数据到队列 public void addQueue(int n) { // 判断队列是否满 if (isFull()){ System.out.println("队列满,不能加入数据~~"); return; } rear++; arr[rear] = n; } // 数据出队列 public int getQueue(){ // 判断队列是否为空 if (isEmpty()){ // 通过抛出异常 throw new RuntimeException("队列为空,不能取数据~~"); } front++; return arr[front]; } // 显示队列的所有数据 public void showQueue() { // 遍历 if(isEmpty()){ System.out.println("队列空的,没有数据~~"); return; } for (int i = 0; i < arr.length; i++) { System.out.printf("arr[%d] = %d\n", i, arr[i]); } } // 显示队列的头数据,不是取数据而仅仅是显示 public int headQueue(){ // 判断队列是否为空 if (isEmpty()){ // 通过抛出异常 throw new RuntimeException("队列为空,没有数据~~"); } return arr[front + 1]; } }
此种方式存在的问题和优化方案
- 数组使用一次就不能使用了,没有达到复用的效果
- 使用算法,改成一个环形的队列:取模%
2、环形队列
分析
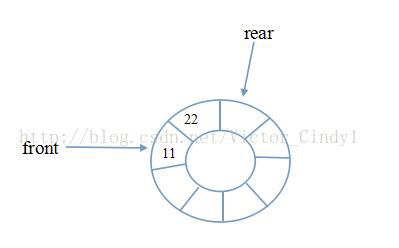
- front就指向队列的头部元素,也就是说arr[front]就是队列的第一个元素,front的初始值 = 0
- rear指向队列的尾部元素的后一个位置,因为希望空出一个空间做为约定,rear的初始值=0
- 当队列满时,条件是
(rear +1) % maxSize= front
【满】- 对队列为空的条件,
rear == front
【空】- 队列中有效的数据的个数
(rear + maxSize - front) % maxSize
【rear=1 front=0,元素个数为1】- 我们就可以在原来的队列上修改得到一个环形队列
代码实现
public class CircleArrayQueueDemo { public static void main(String[] args) { // 创建一个队列 CircleArray circleArray = new CircleArray(4); // 其队列的有效数据最大是3 char key = ' '; // 接受用户输入 Scanner scanner = new Scanner(System.in); boolean loop = true; System.out.println("s(show):显示队列"); System.out.println("e(exit):退出程序"); System.out.println("a(add):添加数据到队列"); System.out.println("g(get):从队列取数据"); System.out.println("h(head):查看队列头的数据"); while (loop) { key = scanner.next().charAt(0); // 接收第一个字符 switch (key) { case 's': circleArray.showQueue(); break; case 'a': System.out.println("输入一个数:"); int value = scanner.nextInt(); circleArray.addQueue(value); break; case 'g': try { int res = circleArray.getQueue(); System.out.printf("取出的数据是%d\n", res); continue; } catch (RuntimeException e){ System.out.println(e.getMessage()); } break; case 'h': try { int res = circleArray.headQueue(); System.out.printf("队列头的数据是%d\n", res); } catch (RuntimeException e){ System.out.println(e.getMessage()); } break; case 'e': scanner.close(); loop = false; break; default: break; } } System.out.println("程序退出"); } } class CircleArray { private int maxSize; // 表示数组的最大容量 private int front; // 队列头的下标,初始值为0 private int rear; // 队列尾的下标的后一个位置,初始值为0 private int[] arr; // 该数据用于存放数据,模拟队列 // 创建队列的构造器 public CircleArray(int maxSize) { this.maxSize = maxSize; arr = new int[maxSize]; front = 0; // 指向队列头部,指向队列头部的数据 rear = 0; // 指向队列尾,指向队列尾部的数据的后一个位置 } // 判断队列是否满 public boolean isFull() { return (rear + 1) % maxSize == front; } // 判断队列是否为空 public boolean isEmpty() { // 因为不是循环队列,头尾不相连,所以rear == front 时队列就为空 return rear == front; } // 添加数据到队列 public void addQueue(int n) { // 判断队列是否满 if (isFull()){ System.out.println("队列满,不能加入数据~~"); return; } // 直接将数据加入 arr[rear] = n; // 将 rear 后移 ,这里必须考虑取模,这是循环的关键,取模算法保证rear永远不会超过maxSize // 最大就是maxSize-1 rear = (rear + 1) % maxSize; } // 数据出队列 public int getQueue(){ // 判断队列是否为空 if (isEmpty()){ // 通过抛出异常 throw new RuntimeException("队列为空,不能取数据~~"); } // front是指向队列的第一个元素 // 1.先把front对应的值保留到一个临时变量,如果考虑释放要设置arr[front] = 0 int value = arr[front]; // 2.将front后移,考虑取模 front = (front + 1) % maxSize; // 3.将临时保存的变量返回 return value; } // 显示队列的所有数据 public void showQueue() { // 遍历 if(isEmpty()){ System.out.println("队列空的,没有数据~~"); return; } // 从front开始遍历,遍历多少个元素 for (int i = front; i < front + size(); i++) { int index = i % maxSize; // 加上size之后可能会超过数组范围,需要进行取模 System.out.printf("arr[%d]=%d\n", index, arr[index]); } } // 求出当前队列的有效数据个数 public int size(){ // 这里 + maxSize保证分子是正数,也可以使用Math.abs(rear - front) return (rear + maxSize - front) % maxSize; } // 显示队列的头数据,不是取数据而仅仅是显示 public int headQueue(){ // 判断队列是否为空 if (isEmpty()){ // 通过抛出异常 throw new RuntimeException("队列为空,没有数据~~"); } return arr[front]; } }
四、链表
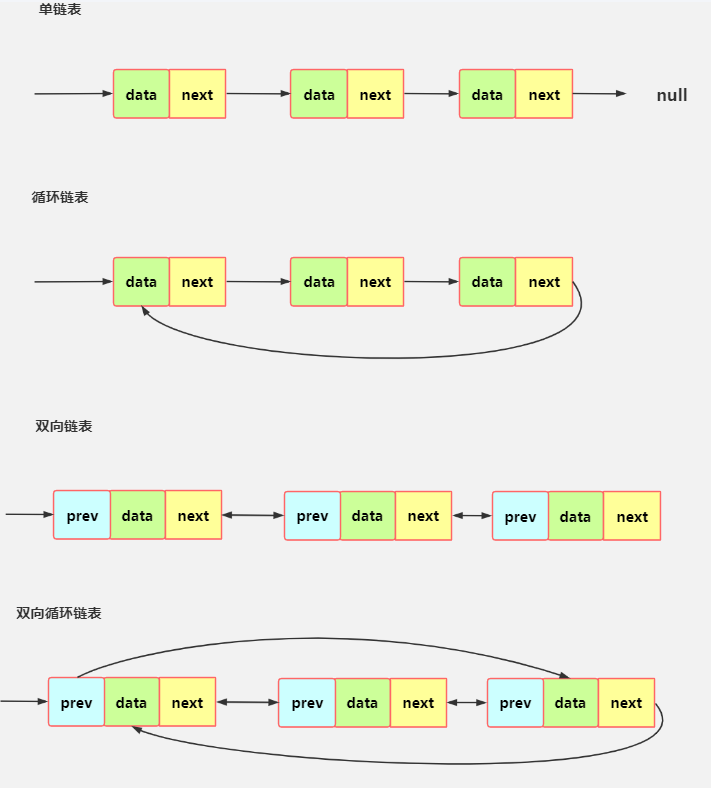
1、单链表
链表是有序的列表,但是它在内存中的存储如下:

链表是以节点的方式来存储, 是
链式存储
每个节点包含 data 域(存储数据),next 域(指向下一个节点)
链表的各个节点不一定是连续存储
链表分为
带头节点的链表和 没有头节点的链表
,根据实际的需求来确定
2、单链表的应用实例
使用带 head 头的单向链表实现 –水浒英雄排行榜管理完成对英雄人物的增删改查操作。
1) 第一种方法在添加英雄时,直接添加到链表的尾部
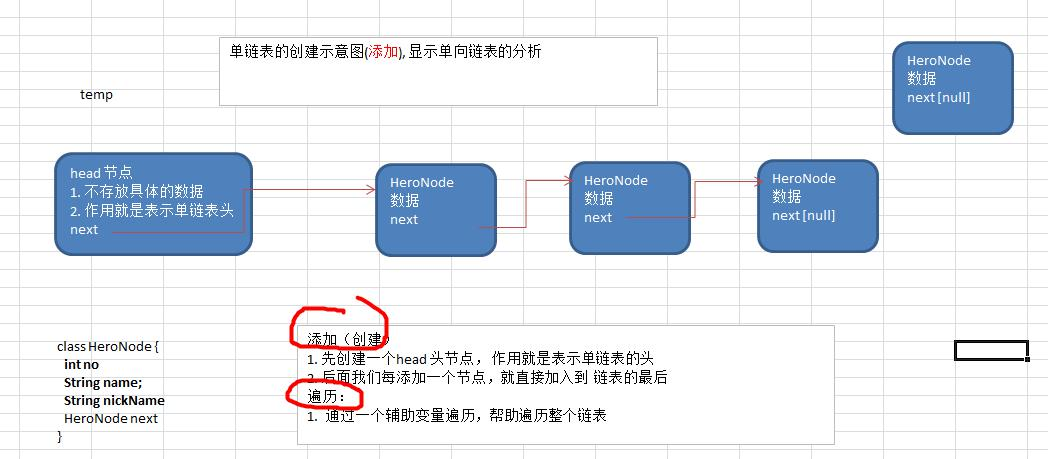
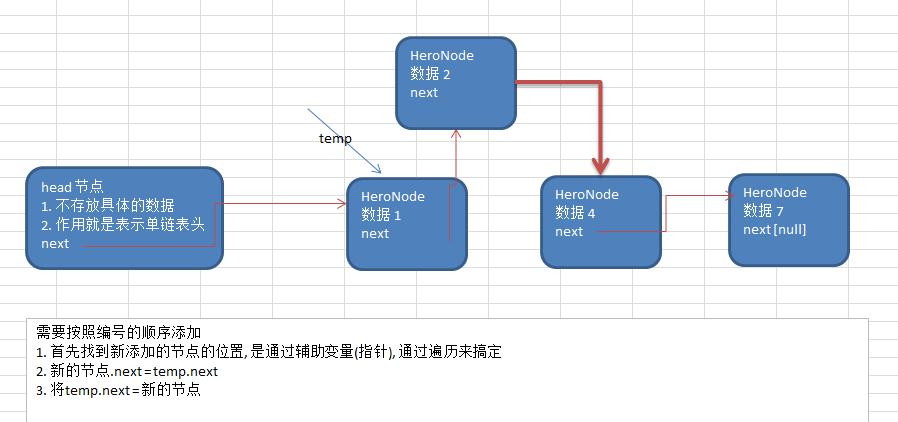
2) 第二种方式在添加英雄时, 根据排名将英雄插入到指定位置(如果有这个排名,则添加失败,并给出提示)
3、第一种方式创建单链表及遍历代码
public class SingleLinkedListDemo { public static void main(String[] args) { SingleLinkedList singleLinkedList = new SingleLinkedList(); HeroNode heroNode = new HeroNode(1, "宋江", "及时雨"); HeroNode heroNode2 = new HeroNode(2, "林冲", "豹子头"); HeroNode heroNode3 = new HeroNode(3, "宋江", "及时雨"); singleLinkedList.add(heroNode); singleLinkedList.add(heroNode3); singleLinkedList.add(heroNode2); singleLinkedList.list(); } } class SingleLinkedList { // 构建头节点 private HeroNode head = new HeroNode(0, "", ""); // 添加方法 public void add(HeroNode heroNode) { // 构建临时变量用来循环,因为头节点不能动 HeroNode temp = head; // 循环遍历找到next为空的节点(next为空的节点就是最后一个节点,并将heroNode赋给最后一个节点.next) while (true) { if (temp.next == null) { break; } // 进行位移操作,向下一个节点移动 temp = temp.next; } // 如果找到了尾节点,退出while循环进行赋值操作 temp.next = heroNode; } // 遍历输出单链表方法 public void list() { if (head.next == null) { System.out.println("链表为空"); return; } // 定义临时变量循环遍历 HeroNode temp = head.next; while (true) { // 判断链表是否到最后,如果到最后就退出 if (temp == null) { break; } // 打印输出每个节点 System.out.println(temp); // 进行位移操作 temp = temp.next; } } } // 构建HeroNode节点 class HeroNode { public int no; // 编号 public String name; // 名称 public String nickName; // 绰号 public HeroNode next; // 下一个节点 public HeroNode(int no, String name, String nickName) { this.no = no; this.name = name; this.nickName = nickName; } @Override public String toString() { return "HeroNode{" + "no=" + no + ", name='" + name + '\'' + ", nickName='" + nickName + '\'' + '}'; } }
4、第二种排序方式创建单链表代码
// 第二种排序添加方法 public void add2(HeroNode heroNode) { // 构建临时变量用来循环,因为头节点不能动 HeroNode temp = head; // 再定义一个变量用来临时存储节点信息 HeroNode temp2 = head; // 循环遍历找到节点编号比heroNode节点编号大的节点 while (true) { // 如果遍历到尾节点那么退出循环 if(temp.next == null){ break; } // 如果编号相同,提示不能插入 if (temp.next.no == heroNode.no){ throw new RuntimeException("不能加入相同编号的数据"); } // 找到那个节点编号比heroNode节点编号大的节点 if(temp.next.no > heroNode.no){ temp2 = temp.next; // 让那个节点的前一个节点重新指向新插入的节点 temp.next = heroNode; // 让新插入的节点的next指向那个节点 heroNode.next = temp2; break; } // 进行位移操作,向下一个节点移动 temp = temp.next; } // 如果遍历没有找到比heroNode节点编号大的节点,那么直接在尾部插入就好了 temp.next = heroNode; }
5、单链表的删除与修改代码
// 删除节点 public void delete(int no) { HeroNode2 temp = head; boolean flag = false; // 标志是否找到待删除节点 while (true) { if (temp.next == null) { // 已经到节点的最后 break; } if (temp.next.no == no) { // 找到待删除节点的前一个节点temp flag = true; break; } temp = temp.next; } // 判断flag if (flag) { // 找到 // 可以删除 temp.next = temp.next.next; } else { System.out.printf("要删除的 %d 节点不存在\n", no); } } // 修改节点方法 public void put(HeroNode heroNode){ // 定义临时变量循环遍历 HeroNode temp = head; if (temp.next == null) { System.out.println("链表为空,不能修改"); return; } // 定义一个布尔变量表示是否找到 boolean flag = false; // 循环遍历找到那个要修改的节点 while(true){ // 到为尾节点退出循环 if(temp.next == null){ break; } if (temp.no == heroNode.no){ flag = true; break; } temp = temp.next; } // 如果找到,退出循环并修改节点 if(flag){ temp.name = heroNode.name; temp.nickName = heroNode.nickName; }else{ System.out.println("没有该节点"); } }
6、单向链表的缺点分析
- 单向链表,
查找的方向只能是一个方向
,而双向链 表可以向前或者向后查找- 单向链表不能自我删除,需要靠辅助节点 ,而双向 链表,则可以
自我删除
,所以前面我们单链表删除 时节点,总是找到temp,temp是待删除节点的前一 个节点
7、双向链表分析
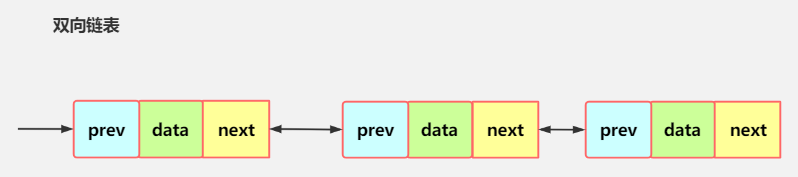
分析 双向链表的遍历,添加,修改,删除的操作思路
遍历
方法和单链表一样,只是可以向前,也可以向后查找
添加
(默认添加到双向链表的最后)
- 先找到双向链表的最后这个节点
- temp.next = newHeroNode
- newHeroNode.pre = temp
修改
思路和 原来的单向链表一样
删除
- 因为是双向链表,因此可以实现自我删除某个节点
- 直接找到要删除的这个节点,比如 temp
- temp.pre.next = temp.next
- temp.next.pre = temp.pre
8、代码(跟单链表差不多,没啥变化)
package com.example.spring.数据结构与算法.双向链表; public class DoubleLinkedListDemo { public static void main(String[] args) { DoubleLinkedList doubleLinkedList = new DoubleLinkedList(); HeroNode2 heroNode = new HeroNode2(8, "宋江", "及时雨"); HeroNode2 heroNode2 = new HeroNode2(1, "林冲", "豹子头"); HeroNode2 heroNode3= new HeroNode2(3, "吴用", "鲁智深"); HeroNode2 heroNode4 = new HeroNode2(6, "吴用", "鲁智深"); HeroNode2 heroNode5= new HeroNode2(9, "吴用", "鲁智深"); HeroNode2 heroNode6= new HeroNode2(2, "吴用", "鲁智深"); doubleLinkedList.add2(heroNode); doubleLinkedList.add2(heroNode2); doubleLinkedList.add2(heroNode3); doubleLinkedList.add2(heroNode4); doubleLinkedList.add2(heroNode5); doubleLinkedList.add2(heroNode6); doubleLinkedList.list(); // doubleLinkedList.delete(3); // doubleLinkedList.list(); // doubleLinkedList.put(new HeroNode2(3,"abc","abc")); // doubleLinkedList.list(); } } class DoubleLinkedList { // 构建头节点 private HeroNode2 head = new HeroNode2(0, "", ""); // 添加方法 public void add(HeroNode2 heroNode2){ // 构建临时变量用来循环,因为头节点不能动 HeroNode2 temp = head; // 循环遍历找到next为空的节点(next为空的节点就是最后一个节点,并将HeroNode2赋给最后一个节点.next) while (true) { if (temp.next == null) { break; } // 进行位移操作,向下一个节点移动 temp = temp.next; } // 如果找到了尾节点,退出while循环进行赋值操作 temp.next = heroNode2; heroNode2.prey = temp; } // 添加排序方法 public void add2(HeroNode2 heroNode2){ // 构建临时变量用来循环,因为头节点不能动 HeroNode2 temp = head; // 再定义一个变量用来临时存储节点信息 HeroNode2 temp2 = head; // 循环遍历找到节点编号比HeroNode2节点编号大的节点 while (true) { // 如果遍历到尾节点那么退出循环 if(temp.next == null){ break; } // 如果编号相同,提示不能插入 if (temp.next.no == heroNode2.no){ throw new RuntimeException("不能加入相同编号的数据"); } // 找到那个节点编号比HeroNode2节点编号大的节点 if(temp.next.no > heroNode2.no){ temp2 = temp.next; // 让那个节点的前一个节点重新指向新插入的节点 temp.next = heroNode2; // 让新插入的节点的next指向那个节点 heroNode2.next = temp2; break; } // 进行位移操作,向下一个节点移动 temp = temp.next; } // 如果遍历没有找到比HeroNode2节点编号大的节点,那么直接在尾部插入就好了 temp.next = heroNode2; } // 遍历输出双链表方法 public void list() { if (head.next == null) { System.out.println("链表为空"); return; } // 定义临时变量循环遍历 HeroNode2 temp = head.next; while (true) { // 判断链表是否到最后,如果到最后就退出 if (temp == null) { break; } // 打印输出每个节点 System.out.println(temp); // 进行位移操作 temp = temp.next; } } // 删除节点 public void delete(int no) { HeroNode2 temp = head.next; boolean flag = false; // 标志是否找到待删除节点 while (true) { if (temp == null) { // 已经到节点的最后 break; } if (temp.no == no) { // 找到待删除节点的前一个节点temp flag = true; break; } temp = temp.next; } // 判断flag if (flag) { // 找到 // 可以删除,重新连接链表结构 temp.prey.next =temp.next; temp.next.prey =temp.prey; } else { System.out.printf("要删除的 %d 节点不存在\n", no); } } // 修改节点方法 public void put(HeroNode2 heroNode){ // 定义临时变量循环遍历 HeroNode2 temp = head; if (temp.next == null) { System.out.println("链表为空,不能修改"); return; } // 定义一个布尔变量表示是否找到 boolean flag = false; // 循环遍历找到那个要修改的节点 while(true){ // 到为尾节点退出循环 if(temp == null){ break; } if (temp.no == heroNode.no){ flag = true; break; } temp = temp.next; } // 如果找到,退出循环并修改节点 if(flag){ temp.name = heroNode.name; temp.nickName = heroNode.nickName; }else{ System.out.println("没有该节点"); } } } // 构建HeroNode2节点 class HeroNode2 { public int no; // 编号 public String name; // 名称 public String nickName; // 绰号 public HeroNode2 next; // 下一个节点 public HeroNode2 prey; // 上一个节点 public HeroNode2(int no, String name, String nickName) { this.no = no; this.name = name; this.nickName = nickName; } @Override public String toString() { return "HeroNode2{" + "no=" + no + ", name='" + name + '\'' + ", nickName='" + nickName + '\'' + '}'; } }
9、单向环形链表

Josephu(约瑟夫、约瑟夫环) 问题 Josephu 问题为:设编号为 1,2,… n 的 n 个人围坐一圈,约定编号为 k(1<=k<=n)的人从 1 开始报数,数 到 m 的那个人出列,它的下一位又从 1 开始报数,数到 m 的那个人又出列,依次类推,直到所有人出列为止,由此产生一个出队编号的序列。
10、算法分析
- 根据用户的输入,生成一个小孩出圈的顺序
- n=7,即有7个人
- k=1,从第1个人开始报数
- m=3,每次数3下
- 需求创建一个辅助指针(变量)helper,事先应该指向环形链表的最后这一个节点
- 小孩报数前,先让first和helper指针同时移动m-1此
- 当这个小孩报数的时候,让first和hepler指针同时的移动m-1次
first = first.getNext()
helper.setNext(first)
- 原来的first指向的节点就没有了任何引用(计数无法解决循环引用的问题,现在JVM都不使用引用计数算法了,不过这样确实会通过可达性分析算法被回收,是不可达对象)
11、代码
public class Josepfu { public static void main(String[] args) { // 测试构建环形链表和遍历 CircleSingleLinkedList circleSingleLinkedList = new CircleSingleLinkedList(); // 加入7个小孩 circleSingleLinkedList.addBoy(7); circleSingleLinkedList.showBoy(); // 测试小孩出圈 3->6->2->7->5->1->4 circleSingleLinkedList.countBoy(1, 3, 7); } } /** * 创建一个环形的单向链表 */ class CircleSingleLinkedList { /** * 创建一个first节点,当前没有编号 */ private Boy first = null; /** * 添加小孩节点,构建一个环形链表 * @param nums */ public void addBoy(int nums) { // nums做一个数据校验 if (nums < 1) { System.out.println("nums的值不正确"); } // 辅助指针,帮助构建环形链表 Boy temp = null; // 使用for来创建我们的环形链表 for (int i = 1; i <= nums; i++) { // 根据编号,创建小孩节点 Boy boy = new Boy(i); // 如果是第一个小孩 if (i == 1) { first = boy; // 构成环 first.setNext(first); // 让temp指向第一个小孩 temp = first; } else { temp.setNext(boy); boy.setNext(first); temp = boy; } } } /** * 遍历当前的环形链表 */ public void showBoy() { // 判断链表是否为空 if (first == null) { System.out.println("没有任何小孩~"); return; } // 因为first不能动,所以我们还需要使用一个辅助指针完成遍历 Boy temp = first; while (true) { System.out.printf("小孩的编号%d \n", temp.getNo()); // 说明遍历完毕 if (temp.getNext() == first){ break; } // temp后移 temp = temp.getNext(); } } /** * 根据用户的输入,计算出小孩出圈的顺序 * @param firstNo 表示小孩从第几个小孩开始报数 * @param countNum 表示一次数几下 * @param nums 表示最初有多少个小孩在圈中 */ public void countBoy(int firstNo, int countNum, int nums) { // 先对数据进行校验 if (first == null || firstNo < 1 || firstNo > nums) { System.out.println("参数输入有误,请重新输入"); return; } // 创建辅助指针 Boy helper = first; // 需求创建一个辅助指针变量helper,事先应该指向环形链表的最后这个节点 while (true) { // 说明helper指向了最后小孩节点 if (helper.getNext() == first) { break; } helper = helper.getNext(); } // 小孩报数前,先让first和helper移动firstNo-1次 for (int j = 0; j < firstNo - 1; j++) { first = first.getNext(); helper = helper.getNext(); } // 当小孩报数时,,让first和helper指针同时移动m-1此,然后出圈 while (true) { // 说明圈中只有一节点 if (helper == first) { break; } // 让first和helper指针同时的移动countNum-1 for (int j = 0; j < countNum - 1; j++) { first = first.getNext(); helper = helper.getNext(); } // 这时first指向的节点,就是小孩要出圈的节点 System.out.printf("小孩%d出圈\n", first.getNo()); // 这是将first指向的小孩出圈 first = first.getNext(); helper.setNext(first); } System.out.printf("最后留在圈中的小孩编号%d\n", first.getNo()); } } /** * 创建一个Boy类,表示一个节点 */ class Boy { /** * 编号 */ private int no; /** * 指向下一个节点,默认为null */ private Boy next; public Boy(int no) { this.no = no; } public int getNo() { return no; } public void setNo(int no) { this.no = no; } public Boy getNext() { return next; } public void setNext(Boy next) { this.next = next; } }
五、栈
1、表达式计算
输入一个表达式
7*2*2-5+1-5+3-3
,对于计算机而言,它接收到的就是一个字符串,通过栈的思想可以获得表达式的计算结果
2、栈的介绍
- 栈的英文为(stack)
- 栈是一个
先入后出(FIFO——First In Last Out)
的有序列表- 栈(stack)是限制线性表中元素的插入和删除
只能在线性表的同一端
进行的一种特殊的线性表。允许插入和删除的一端,为变化的一端,称为
栈顶(Top)
,另一端为固定的一端,称为
栈底(Bottom)
- 根据栈的定义可知,最先放入栈中元素在栈底,最后放入的元素在栈顶;而删除元素刚好相反,最后放入的元素最先删除,最先放入的元素最后删除
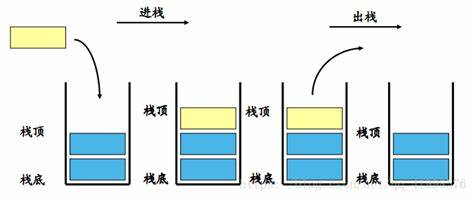
3、栈的应用场景
- 子程序的调用:在跳往子程序前,会先将下个指令的地址存到堆栈中,直到子程序执行完后再将地址取出,以回到原来的程序中
- 处理参数递归调用:和子程序的调用类似,只是除了存储下一个指令的地址外,也将参数、区域变量等数据存入堆栈中
- 表达式的转换【中缀表达式转后缀表达式】和求值(实际解决)
- 二叉树的遍历
- 图形的深度优先(depth——first)搜索法
4、代码实现(数组)
public class ArrayStackDemo { public static void main(String[] args) { // 测试 // 先创建一个ArrayStack ——> 表示栈 ArrayStack stack = new ArrayStack(4); String key = ""; // 控制是否退出菜单 boolean loop = true; Scanner scanner = new Scanner(System.in);System.out.println("show:表示显示栈"); System.out.println("exit:表示退出程序"); System.out.println("push:表示添加数据到栈(入栈)"); System.out.println("pop:表示从栈取出数据(出栈)"); while (loop) { System.out.println("请输入你的选择:"); key = scanner.next(); switch (key) { case "show": stack.list(); break; case "push": System.out.println("请输入一个数字:"); int value = scanner.nextInt(); stack.push(value); break; case "pop": try { int res = stack.pop(); System.out.printf("出栈的数据是%d\n", res); } catch (Exception e) { System.out.println(e.getMessage()); } break; case "exit": scanner.close(); loop = false; break; default: break; } } System.out.println("程序退出~~"); } } /** * 定义一个ArrayStack表示栈 */ class ArrayStack{ /** * 栈的大小 */ private int maxSize; /** * 数组,数组模拟栈,数组就放在该数组 */ private int[] stack; /** * top表示栈顶,初始化为-1 */ private int top = -1; /** * 构造器 * @param maxSize 栈的最大容量 */ public ArrayStack(int maxSize) { this.maxSize = maxSize; stack = new int[maxSize]; } /** * 栈满 * @return 是否栈满 */ public boolean isFull() { return top == maxSize - 1; } /** * 栈空 * @return 是否为空 */ public boolean isEmpty() { return top == -1; } /** * 入栈 * @param value 入栈的值 */ public void push(int value) { // 先判断栈是否满 if (isFull()) { System.out.println("栈满"); return; } top++; stack[top] = value; } /** * 出栈 * @return int 出栈的值 */ public int pop() { // 先判断栈是否为空 if (isEmpty()) { // 抛出异常 throw new RuntimeException("栈空"); } int value = stack[top]; top--; return value; } /** * 显示栈的情况,遍历时需要从栈顶开始显示数据 */ public void list() { if (isEmpty()) { System.out.println("栈空,没有数据~"); return; } for (int i = top; i >= 0; i--) { System.out.printf("stack【%d】 = %d\n", i, stack[i]); } } }
5、栈实现计算器(中缀)

- 初始化两个栈,一个【数栈】和一个【符号栈】
- 通过一个index值(索引),来遍历我们的表达式
- 如果发现是一个数字,就直接入【数栈】
- 如果发现是一个运算符,就分情况讨论
- 如果当前的【符号栈】为空,那就直接入栈
- 如果当前的【符号栈】有操作符,就进行比较
- 【当前的操作符】的优先级 <= 【符号栈中操作符】的优先级,就需要从【数栈】中pop出两个数,再从【符号栈】中pop出一个符号,然后进行运算,将得到结果入【数栈】,再递归调用步骤3
- 【当前的操作符】的优先级 > 【符号栈中操作符】的优先级,就直接入符号栈
- 当表达式扫描完毕,就顺序的从【数栈】和【符号栈】中pop相应的数和符号,并运行
- 最从【数栈】中只有一个数字就是表达式的结果
6、代码实现(中缀表达式计算器)
public class Calculator { public static void main(String[] args) { // 测试运算 String expression1 = "33+2+2*6-2"; String expression2 = "7*22*2-5+1-5+3-4"; String expression3 = "4/2*3-4*2-3-99"; String expression4 = "1*1*1*3*2/3"; String expression5 = "11*1*1*3*2/3"; String expression6 = "1000*23"; // 创建两个栈:数栈、符号栈 ListStack1 numStack = new ListStack1(10); ListStack1 operationStack = new ListStack1(10); test(expression1, numStack, operationStack); test(expression2, numStack, operationStack); test(expression3, numStack, operationStack); test(expression4, numStack, operationStack); test(expression5, numStack, operationStack); test(expression6, numStack, operationStack); } /** * 测试方法,测试表达式的结果,并且打印结果 * @param expression 表达式 * @param numStack 数字栈 * @param operationStack 符号栈 */ public static void test(String expression, ListStack1 numStack, ListStack1 operationStack) { // 用于扫描 int index = 0; // 将每次扫描得到的char保存到ch char ch = ' '; // 开始while循环的扫描expression while (true) { // 依次得到expression的每一个字符 ch = getCharByIndex(expression, index); // 判断ch是什么,然后做相应的处理 if (isOperation(ch)) { // 运用管道过滤器风格,处理运算符 operationSolve1(ch, numStack, operationStack); } else { // 数直接入数栈,对值为ASCII值-48 // 当处理多位数时候,不能立即入栈,可能是多位数,调用过滤器处理多位数 index = numSolve1(expression, index, numStack); } // 让index+1,并判断是否扫描到expression最后 index++; if (index >= expression.length()) { break; } } // 最后只剩下两个数和一个运算符 int res = cal((int) numStack.pop(), (int) numStack.pop(), (char) operationStack.pop()); System.out.printf("表达式: %s = %d\n", expression, res); } /** * 获取表达式的下标位置为index的字符 * @param expression 表达式 * @param index 下标 * @return */ public static char getCharByIndex(String expression, int index) { return expression.charAt(index); } /** * 处理数字入栈的情况,包含处理多位数的情况,并且返回到操作表达式当前的下标 * @param expression 表达式 * @param index 下标 * @param numStack 数字栈 * @return 新的下标 */ public static int numSolve1(String expression, Integer index, ListStack1 numStack) { int end = index + 1; for (; end < expression.length(); end++) { char ch = getCharByIndex(expression, end); // 判断是不是数字 if (!isOperation(ch)) { continue; } else { break; } } String numStr = expression.substring(index, end); // 数据入栈 numStack.push(Integer.valueOf(numStr)); // 因为test函数进行了+1,所以这里进行-1,避免给重复添加 return end - 1; } /** * 符号过滤器1,判断当前是否具有字符 * @param ch 运算符 * @param numStack 数字栈 * @param operationStack 运算符栈 */ public static void operationSolve1(char ch, ListStack1 numStack, ListStack1 operationStack) { // 判断当前符号栈是否具有操作符 if (!operationStack.isEmpty()) { operationSolve2(ch, numStack, operationStack); return; } else { operationStack.push(ch); return; } } /** * 符号过滤器2,处理字符优先级,递归调用过滤器1 * @param ch 运算符 * @param numStack 数字栈 * @param operationStack 运算符栈 */ public static void operationSolve2(char ch, ListStack1 numStack, ListStack1 operationStack) { // 比较优先级 if (priority(ch) <= priority((Character) operationStack.peek())) { // 调用过滤器3进行计算 operationSolve3(numStack,operationStack); // 递归调用过滤器1,不能递归调用过滤器2,因为可能存在当前运算符栈为空的情况 operationSolve1(ch, numStack, operationStack); return; } else { // 直接将运算符加入到运算符栈中 operationStack.push(ch); return; } } /** * 符号过滤器3,进行运算 * @param numStack 数字栈 * @param operationStack 运算符栈 */ public static void operationSolve3(ListStack1 numStack, ListStack1 operationStack) { // 定义相关变量 int num1 = (int) numStack.pop(); int num2 = (int) numStack.pop(); char operation = (char) operationStack.pop(); int res = cal(num1, num2, operation); // 把运算结果加到数栈 numStack.push(res); return; } /** * 返回运算符的优先级,数字越大,运算符越高 * @param operation 运算符 * @return */ public static int priority(char operation) { if (operation == '*' || operation == '/') { return 1; } else if (operation == '+' || operation == '-') { return 0; } else { // 假设目前的表达式只有 + - * / return -1; } } /** * 判断是不是运算符 * @param val 字符 * @return 是不是运算符 */ public static boolean isOperation(char val) { return val == '+' || val == '-' || val =='*' || val == '/'; } /** * 计算结果 * @param num1 操作数1,先出栈的数 * @param num2 操作数2,后出栈的数 * @param operation 操作符 * @return 计算结果 */ public static int cal(int num1, int num2, char operation) { // 用于存放运算的结果 int res = 0; switch (operation) { case '+': res = num1 + num2; break; case '-': // num1是先弹出来的数,为被减数 res = num2 - num1; break; case '*': res = num1 * num2; break; case '/': // num1是先弹出来的数,为被除数 res = num2 / num1; default: break; } return res; } } /** * 表示链表的一个节点 */ class Node1{ Object element; Node1 next; public Node1(Object element) { this(element, null); } /** * 头插法插入节点 * @param element 新增节点的value * @param n 原来的头节点 */ public Node1(Object element, Node1 n) { this.element = element; next = n; } public Object getElement() { return element; } public void setElement(Object element) { this.element = element; } public Node1 getNext() { return next; } public void setNext(Node1 next) { this.next = next; } } /** * 用链表实现堆栈 */ class ListStack1 { /** * 栈顶元素 */ Node1 header; /** * 栈内元素个数 */ int elementCount; /** * 栈的大小 */ int size; /** * 构造函数,构造一个空的堆栈 */ public ListStack1() { header = null; elementCount = 0; size = 0; } /** * 通过构造器 自定义栈的大小 * @param size 栈的大小 */ public ListStack1(int size) { header = null; elementCount = 0; this.size = size; } /** * 设置堆栈大小 * @param size 堆栈大小 */ public void setSize(int size) { this.size = size; } /** * 设置栈顶元素 * @param header 栈顶元素 */ public void setHeader(Node1 header) { this.header = header; } /** * 获取堆栈长度 * @return 堆栈长度 */ public int getSize() { return size; } /** * 返回栈中元素的个数 * @return 栈中元素的个数 */ public int getElementCount() { return elementCount; } /** * 判断栈是否为空 * @return 如果栈是空的,返回真,否则,返回假 */ public boolean isEmpty() { if (elementCount == 0) { return true; } return false; } /** * 判断栈满 * @return 如果栈是满的,返回真,否则,返回假 */ public boolean isFull() { if (elementCount == size) { return true; } return false; } /** * 把对象入栈 * @param value 对象 */ public void push(Object value) { if (this.isFull()) { throw new RuntimeException("Stack is Full"); } header = new Node1(value, header); elementCount++; } /** * 出栈,并返回被出栈的元素 * @return 被出栈的元素 */ public Object pop() { if (this.isEmpty()) { throw new RuntimeException("Stack is empty"); } Object obj = header.getElement(); header = header.getNext(); elementCount--; return obj; } /** * 返回栈顶元素 * @return 栈顶元素 */ public Object peek() { if (this.isEmpty()) { throw new RuntimeException("Stack is empty"); } return header.getElement(); } }
7、前、中、后缀表达式
前缀表达式(波兰表达式)
- 前缀表达式又称波兰式,前缀表达式的运算符位于操作数之前
- 举例说明:(3+4)*5-6 对应的前缀表达式就是 – * + 3 4 5 6
前缀表达式的计算机求值
从右至左扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(栈顶元素 和 次顶元素),并将结果入栈;重复上述过程直到表达式最左端,最后运算得出的值即为表达式的结果例如 (3+4)×5-6 对应的前缀表达式就是 – × + 3 4 5 6 , 针对前缀表达式求值步骤如下:
- 从
右至左扫描
,将6、5、4、3压入堆栈- 遇到+运算符,因此弹出3和4(3为栈顶元素,4为次顶元素),计算出3+4的值,得7,再将7入栈
- 接下来是×运算符,因此弹出7和5,计算出7×5=35,将35入栈
- 最后是-运算符,计算出35-6的值,即29,由此得出最终结果
中缀表达式
- 中缀表达式就是
常见的运算表达式
,如(3+4)*5-6- 中缀表达式的求值是平常最为熟悉的,但是对计算机说却不好操作(前面我们将的案例就能看出这个问题,)因此,在计算结束时,往往会将中缀表达式转成其它表达式来操作(一般是转成后缀表达式)
后缀表达式(逆波兰表达式)
- 后缀表达式又称
逆波兰表达式
,与前缀表达式相似,只是运算符位于操作数之后- 中举例说明: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 –
正常的表达式 逆波兰表达式 a+b a b + a+(b-c) a b c – + a+(b-c)*d a b c – d * + a+d*(b-c) a d b c – * + a=1+3 a 1 3 + =
后缀表达式的计算机求值
从左至右扫描表达式,遇到数字时,将数字压入堆栈,遇到运算符时,弹出栈顶的两个数,用运算符对它们做相应的计算(次顶元素 和 栈顶元素),并将结果入栈;重复上述过程直到表达式最右端,最后运算得出的值即为表达式的结果
例如: (3+4)×5-6 对应的后缀表达式就是
3 4 + 5 × 6 –
,
针对后缀表达式求值步骤如下:
从左至右扫描,将3和4压入堆栈
遇到+运算符,因此弹出4和3(4为栈顶元素,3为次顶元素),计算出3+4的值,得7,再将7入栈
将5入栈
接下来是×运算符,因此弹出5和7,计算出7×5=35,将35入栈
将6入栈
最后是-运算符,计算出35-6的值,即29,由此得出最终结果
逆波兰计算器代码实现
public class PolandNotation { public static void main(String[] args) { // 定义一个逆波兰表达式 // (3+4)*5-6 => 3 4 + 5 * 6 - String suffixExpression = "3 4 + 5 * 6 -"; // 先将3 4 + 5 * 6 - 放入一个链表,配合栈完成计算 List<String> listString = getListString(suffixExpression); System.out.println(calculate(listString)); } /** * 将逆波兰表达式的数据和运算符依次放到ArrayList中 * @param suffixExpression 逆波兰表达式 * @return 链表 */ public static List<String> getListString(String suffixExpression) { // 将suffixExpression分割 String[] split = suffixExpression.split(" "); List<String> list = new ArrayList<>(); for (String element : split) { list.add(element); } return list; } /** * 计算逆波兰表达式最终结果 * @param stringList 数据和运算符链表 * @return 计算结果 */ public static int calculate(List<String> stringList) { // 创建一个栈即可 Stack<String> stack = new Stack<>(); // 遍历链表 for (String element : stringList){ // 使用正则表达式来取出数,匹配多位数 if (element.matches("\\d+")) { // 入栈 stack.push(element); } else { // pop出两个数,并进行运算再入栈 int num2 = Integer.parseInt(stack.pop()); int num1 = Integer.parseInt(stack.pop()); int res = 0; if (element.equals("+")) { res = num1 + num2; } else if (element.equals("-")) { res = num1 - num2; } else if (element.equals("*")) { res = num1 * num2; } else if (element.equals("/")) { res = num1 / num2; } else { throw new RuntimeException("运算符有误"); } // 把res 入栈 stack.push(res + ""); } } return Integer.valueOf(stack.pop()); } }