上一节笔记:
学弱猹:数值优化|笔记整理(9)——非线性规划的极值性质,KKT条件zhuanlan.zhihu.com
————————————————————————————————————
大家好!非常熟悉我的写作风格的同学知道,标题的A就是10的意思。
在这一节我们会给大家介绍带约束优化中更为具体的
线性规划
的内容。相信大家在运筹学中会对线性规划更加熟悉,比方说单纯形法就是运筹学一开始就会讲授的内容。那么在优化中,我们也会关注它们,通过介绍他们来了解优化在运筹中的应用,也能够让大家更好的了解为什么“运筹优化”一般都放在一起来说。
那么我们开始吧。
目录
-
引入:线性规划的含义及标准形式
- 几何建构
- 单纯形法
-
内点法
- 算法实现
- 实际的算法实现
Source
-
D. G. Luenberger and Y. Ye.
Linear and nonlinear programming
-
J. Nocedal and S. J. Wright,
Numerical Optimization
引入:线性规划的含义及标准形式
相信大家在高中数学的必修五里已经学过一部分的线性规划的知识。这一节我们关注的问题基本上就是下面这个形式
其中
,也就是说,我们的目标函数和约束函数
都是线性的
。
和上一节的非线性规划一样,很多人会有疑问这个约束条件会不会太强,因为毕竟不是所有的问题都是仅有等式约束的。但是实际上不会,因为我们可以通过
松弛变量
(slack variable)和
拆分正负部分
的方式,使得绝大部分问题都可以使用我们这个框架。具体来说,假如我们的问题一开始是
添加松弛变量
,可以得到
再拆分正负号,具体来说就是设
是
的正数部分,而
为
的负数部分,满足
(比方说
,那么
)。那么这样的话,问题就会变成这样的形式
换句话说,我们实际上只需要把我们这个新构造的向量
重新换元为
,就可以完成我们的任务,也就是说所有满足一开始那种线性形式的问题,都可以使用我们的框架来解决。
几何建构
因为线性规划是一个具体的问题,这也为它带来了一定的几何意义。我们先给出它约束的一个几何定义。
Definition 1: Hyperplane
定义
是一个超平面。其中
,
。
比方说
就是一个与
垂直的所有向量的集合。如果只改变
,那么形成的各个超平面相互平行。这也不难理解,因为比方说如果
,那就是我们高中就已经学过的直线的斜截式方程。而对应到
,那就会变成我们解析几何中学过的平面方程,再往上因为人脑无法再直观想象出来这种结构了,就给了它一个超平面的名字,但是我们如果把它投影到一个低维的空间上(比方说三维空间),其实依然是满足平面的结构的。
定义完超平面自然会有超平面衍生出来的一些几何形状。
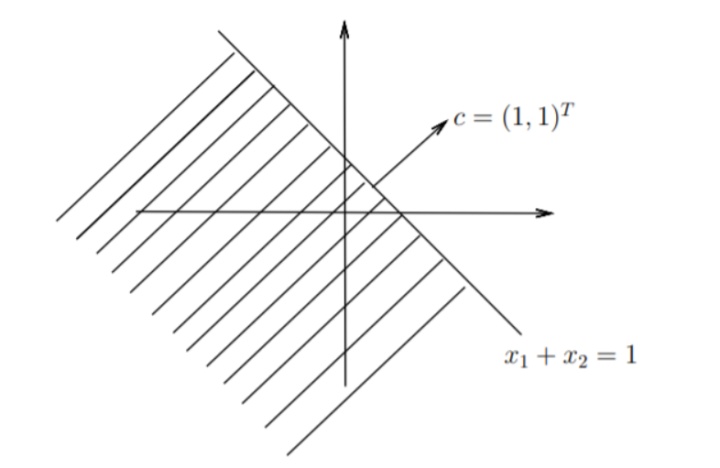
Definition 2: Half Space
定义
是由
定义出来的半平面。其中
一定沿着可行域的外方向。
这里我们可以拿一个
的直线来举例子。
这两个性质为我们后面分析优化问题提供了很多理解上的方便。
接下来我们会给出一个与凸集有关的概念。
Definition 3: Extreme Point
设
为一个凸集,且
,那么如果不存在
,使得存在
满足
,那么称
是一个极值点。
这里的翻译上要注意,和我们之前说的“极小值”,”极大值“
并不是一个意思
,根据单词extreme的含义,可以看出它比较像“边界上的点”的意思。
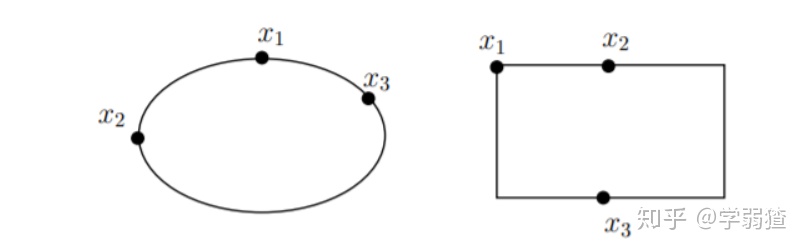
对于下面的这张图,我们认为它们的约束都是实心的。我们可以看出,左边这个椭圆的三个点都是极值点,但是对于右边来说,只有点
是极值点,剩下的两个都不是。
定义超平面的原因在于,我们的最终的约束
,是一个线性方程组,也就是说可以视为是
一系列超平面的交集
。而这样的几何图形也是有自己的名字的。
Definition 4: Polytope, Polyhedron
定义有限个闭半空间的交为凸多胞体。定义非空有界的凸多胞体为凸多面体。
这里要注意的是,polytope和polyhedron其实都可以被翻译为多面体,在这里为了区分我们将polytope翻译成了多胞体,polyhedron翻译成了多面体。虽然网上说多胞体一般是用来形容
维空间下的图形,而多面体一般只考虑三维情况,但在这里很明显,至少从定义上来说二者并没有这样的区分。因此我们这里多解释一些,并且在之后我们还是会保留这两个定义的原版英文。
接下来我们给出一个与单纯形法紧密相关的性质。
Proposition 1:
若
是一个凸的polyhedron,那么
会在极值点上取到极小值。
这个性质我们不详细证明,大家可以利用凸的定义观察到,如果不是极值点就一定可以找到更小的值。
好的,有了这些铺垫,我们就可以慢慢的给出单纯形法的做法了。
单纯形法
我们要注意的是,我们的标准形式就蕴含着说,我们的约束就是
多个超平面的交
,因为
。也可以看出我们的集合
也是一个凸集,而单纯形法的重要的支撑在于下面这个定理。
Theorem 1:
是优化问题的解当且仅当
是极值点。
这个证明还是有点复杂的,可以参考D. G. Luenberger and Y. Ye.的
Linear and Nonlinear Programming
的P23。而这个定理就是想告诉我们,我们只需要使得点位于极值点,就可以找到极小值,单纯形法的核心,就是
找遍所有的极值点
。
但是如何做到这样的事情呢?还是一样,
从源头找思路
。在正常的情况下,我们的约束都是不等式约束,是
添加了松弛变量
才使得我们可以化简为标准的形式。所以为什么叫松弛变量呢?不就是因为它很多时候起不到作用吗?那么什么叫起不到作用呢?简单来说,就是
对应的解向量的分量为0
。为了理解这个含义,我们的做法是对不同的
的列做一个线性变换,使得我们可以找出这个矩阵对应的线性变换中,冗余的部分。也就是说我们考虑设一个正交矩阵
,使得
其中
。并且
是满秩的(否则的话就没解了)。这样做之后,根据正交矩阵的性质我们有
,所以设
就可以得到
设
,那么会有
这里我们有一个操作,就是人工设置我们的
。为什么可以这么做?如果只是图一个简单,那么只需要理解我们
人工的认为
的部分是松弛变量即可
。但是严谨的来说,首先,如果
,那么会出现什么?不妨假设某一个分量是非零的,那么注意到,我们一定可以说明它不是极点,因为假如说我们可以变换一下
,得到一个新的点
,就可以得到
这里
不需要事先计算出来,就假设
是已知的
简单变一下我们就可以得到
这样的话,只需要设
,
,就可以得到两个点,并且满足凸集的性质。这里能够成功的原因就是我们的假设
,因为当
的时候,是不能够保证我们的
是不同的。
既然有了推论,我们的
也就自然可以算出来,取个逆就可以了。
到此为止,我们可以发现,如果我们达到了一个极值点,那么必然有
。虽然这个是经过一组线性变换之后的新的
,但是这个变换,无非就是挑出了一组方程组中的基而已。换句话说,我们去掉这一组基的一个分量,换成之前不属于基的某一个分量,依然可以组成一组基。所以我们这里的松弛变量是
可以换的
,而这个更换就会得到不同的极值点。
单纯形法就是这么一个思路,不停的枚举可能的极值点,直到我们的目标函数值无法下降为止。但是如何判断呢?自然不可能真的是暴力枚举。现在设想一下两个不同的方程组
并且我们认为一开始有
,但是经过了一组“换基”,使得
(换基的含义我们后面会有例子可以进行更加形象的解释,在这里你可以理解为,
这两个分别挑出了一列交换了一下),化简就可以得到
那么对应到我们的目标函数呢?其实就是
这里
,我们可以看到这个值是很重要的,因为如果
,那么这个变换就是无效的,因为无法使得函数下降。所以换句话说,如果我们无论怎么换基,都有
,就说明找到极小值了,算法也就应该结束了。
到此,我们可以总结一下我们的算法核心的步骤了
找到
中,
的分量为负且绝对值最大的那个对应的指标。设这个指标为
,并设置
,也就是说考虑将这个分量由
改为
。让
满足
中最小的分量为0设
是
中分量被变为0的那个指标交换这两个指标,也就是交换
列得到新的
,进行下一轮操作。
那么我们来举个例子吧,演示几步过程就自然会对这个算法理解的更加透彻了。
Example 1:
考虑问题
,约束条件为
按照我们这里的想法,我们自然的是希望把我们的不等式组通过矩阵的方式写出来,在这里其实就是写成
那么我们可以很容易的挑出我们
矩阵中的一组基,这里就是系数矩阵的第3,4列,所以我们可以写出
,且
,所以可以得到我们的
。
根据我们的算法,既然我们设置了
为基,潜在意思就是
,所以我们这里的候选的
,因此对应的可以得到
。
注意到我们的
,因此结合我们的
,我们可以得到
,也就是说第一个指标是负的指标中,绝对值最大的那个。因此我们考虑要换基,把基中的第一个分量给换进去,因为如果它作为基,就可以使得函数值进一步下降(运筹学中有一个说法叫做
入基
)。
要入基的话,就是设
,所以对应的要计算一个合适的
。这里我们可以得到
,也就是说这里的
,因为在这个情况下,可以满足
,且存在一个分量到达了0的边界。换句话说,这个时候分量为0的部分就是应该被视为“松弛变量”的部分,应该把基的这个分量换出去(也叫
出基
)。
在更换完之后,可以得到新的
为
,对应的
,所以可以得到新的
,所以对应的
(注意这个时候
对应的列指标已经变了,所以拼接的时候要注意顺序),这个时候也可以算出来
。那么一直往下做,到停止条件满足即可。
事实上在运筹学中,我们也可以通过
画表
的方式来解决这样的问题,思路也完全一样。这里我们因为长度限制,就不多说这个思路了,可以参考运筹学的教材来了解这样的计算方法。
所以到此为止,所有的单纯形法的“正常”计算思路都已经介绍完了,但是事实上还会有一种情况就是
退化
。这个的意思是,
当我们的基确定下来之后,
中却存在
的分量为0
。换句话说这个时候只有
,就没有办法使得算法正常进行。对于退化自然也有一定的处理方式,但同样的我们也不在这里详细介绍。同时如果我们的过程是正常的,那么算法结束的时候,就是找到了极小值的时候。这个可以在
Numerical Optimization
中的Thm 13.4中找到。
内点法
刚刚我们介绍完了单纯形法,但是单纯形法并非是一个速度很让人满意的方法。假如说我们的
的大小为
,那么它大概需要
到
的迭代次数,这样的话其实严格来说算是一个
指数级别复杂度
的算法(注意一下,严格来说计算时间复杂度的计算方式是根据
数据的存储量
而言的,而存储一个
这个数到计算机自然不可能占用
个字节,所以这里大家可能会有疑惑,记住这个结论就好)。所以相比较而言,内点法(Interior Point Method)就是一个值得提倡的方法,因为它的计算复杂度
一般是多项式级别
。
还是一样,考虑问题
且
行满秩。内点法的含义就是
根据方程组的KKT条件,寻找它的一个满足KKT条件的点
。比方说在这里的拉格朗日函数为
其中
,那么对应的它的KKT条件为
大家可以通过第一节的向量求导的方法来求解KKT条件,这里为了方便把传送门放上:
学弱猹:数值优化|笔记整理(1)——引入,线搜索:步长选取条件zhuanlan.zhihu.com

所以化简一下可以得到我们关注的问题的形式为
并且
,
。
仔细观察这个方程组可以发现,这个本质上就是一个
的
方程组求根
问题。对于方程组求根,我们本质上就是求解下面这样的问题
其中
为方程组的Jacobi矩阵,在这里其实就是
,也就是我们的每一行都是对它的三个分量
求梯度得到的结果。这个结果的由来也并不难理解,具体的可以参考牛顿法(第5节)的推导,然后把它从方程推广到方程组的情况。这里还是一样给出链接
学弱猹:数值优化(5)——信赖域子问题的求解,牛顿法及其拓展zhuanlan.zhihu.com

而这个方程组的求解一般也确实是牛顿法。
假如说我们定下来了
,那么本质上其实就是定下了我们的
搜索方向
。换句话说我们的更新公式就是
很明显,为了保证
的非负性,我们需要让
小一些。但是这也就是问题所在了。因为这个条件会让我们的收敛速度很慢。同时需要注意的是,我们的迭代矩阵
不一定是满秩的
,这样的话方程组的解不一定唯一,对应的搜索方向也会无法确定。
为了使得我们的解是唯一的,一个关键的思路是考虑修改我们的方程组,变成下面这样
所以一定程度上是放宽了互补松弛条件。
当然了这个思路不是拍脑袋一下子想出来的,其背后是将这个线性规划问题修改成了一个对数栅栏(log-barrier,这个翻译实在是太烫嘴了)的形式。所以本质上就是
这个函数是一个严格凸的函数,所以极小值唯一。同时需要注意的是,因为它满足LICQ条件(大家可以自己验证一下),所以它的Lagrange函数的解是唯一的。而如果我们求解它的KKT条件,我们可以得到
然后设
,化简即可得到我们之前的形式。之后的方式就很明确了。精确的求解结果得不到,那就考虑近似,也就是说不断的减小
就可以了。
算法实现
理论的部分其实到此就差不多了,接下来我们介绍实际的算法中,它会怎么做。首先要观察到的是,
本质上是一个对于
(意思就是
的对应分量的积)的估计,所以我们这里的算法思路就是设
,然后设
是一个对于当前的
的估计,再人工控制
(一般来说
),这样的话这个
随着
的变小,也就自然的会变小。所以最终算法需要求解的问题,就是
当然了,对这个方程组,我们不会真的构造这样的一个大矩阵,而是会考虑把它化为下面这样的等价形式来求解。
其中
,
,
。
看似很玄乎,其实就是把三个式子写出来然后尝试着去化简而已。先根据原始方程组得到的3个式子来,然后先得到比较简单的
,这就会用到两个方程,然后把式子带到最后一个方程里面化简即可。注意根据定义,我们可以得到
。
好的,接下来我们贴出我们的算法图给大家参考。

这里有一个疑点就是
,事实上,这个集合被定义为
,简单来说就是希望我们的每一个分量值在一个合适的范围内。下面这一张图虽然不太严谨,但算解释了这一点。
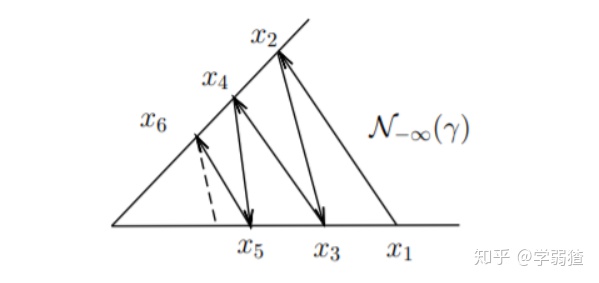
也就是说,这个算法一方面希望函数值能够尽可能的下降,另一方面又不希望算法让我们的迭代点不满足约束条件。事实上,这就会导致一般情况下,算法跑出来的点的轨迹就如上图所示。
那么这个算法的收敛性如何呢?可以参考下面的这个性质。
Theorem 2:
设
为算法所定义出的对应含义的序列,那么给定
,存在一个
,有
我们这里不给出证明,感兴趣的读者可以参考
Numerical Optimization
的定理14.4。
实际的算法实现
有的人可能会感到一脸懵逼:
理论我也知道了,算法我也知道了,那这一块是什么?其实虽然说书上给了我们上面贴的算法,但是实际情况下,大家为了效果会更希望用我们接下来提供的方法,尽管它并没有理论保障。但是这里要提醒大家的是,这种现象在带约束优化问题中是常态
。之后我们还会碰到这样的情况。
因为没有理论基础,我们也不多解释这个算法,大家如果想实现的话,直接使用即可。


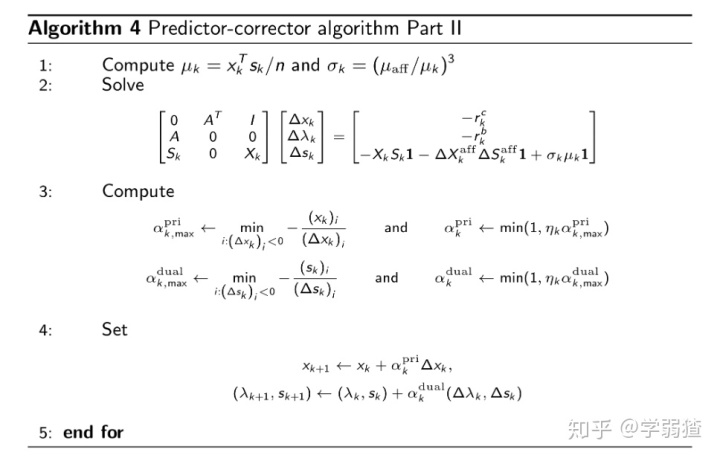
这个方法的核心思想是
主对偶问题
(primal-dual)优化方法,简单的用凸优化的知识来解释呢,就是
对偶问题和原始问题都做优化迭代
。
好的,关于内点法,我们就说到这里。
小结
本节我们关注的是线性规划中的两个方法:单纯形法与内点法。这两种方法的来源不太一样,一个是考虑的几何意义,一个是考虑的KKT条件(当然了其实单纯形法也可以从KKT条件的角度出发解释,不过不是我们这里采用的考虑方法)。二者的思路不同,求解的方式也有不一样。当然了,在内点法中更是出现了实际的使用方法没有理论保障的情况。这也会是之后的常态。
在下一节我们会介绍
二次规划
的具体的算法,大家可以将它与线性规划对比,看看二者有什么区别。
小结
本节我们主要关注了非线性规划问题的极值性质,从一开始对于约束的探索,到之后搭建几何到代数的桥梁,再到最后利用这些思想方法证明带约束优化中极为重要的KKT条件。虽然说KKT条件只是一个充分条件,很像是无约束优化中的驻点的地位,但是对于优化这个领域来说,这已经算是很不错的成果了。
下一节我们会进入到
线性规划
的部分,介绍一些运筹学中很常见的算法,并适当的给出一些实际的计算实例。
——————————————————————————————————————

本专栏为我的个人专栏,也是我学习笔记的主要生产地。
任何笔记都具有著作权,不可随意转载和剽窃
。
个人微信公众号:
cha-diary
,你可以通过它来获得最新文章更新的通知。
《一个大学生的日常笔记》专栏目录:笔记专栏|目录
《GetDataWet》专栏目录:GetDataWet|目录
想要更多方面的知识分享吗?可以关注专栏:一个大学生的日常笔记。你既可以在那里找到通俗易懂的数学,也可以找到一些杂谈和闲聊。也可以关注专栏:GetDataWet,看看在大数据的世界中,一个人的心路历程。我鼓励和我相似的同志们投稿于此,增加专栏的多元性,让更多相似的求知者受益~