问题:
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色,每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。这个问题是图的m可着色判定问题。若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色,则称这个数m为该图的色数。求一个图的色数m的问题称为图的m可着色优化问题。
回溯法:
回溯法是蛮力法的改进。基于深度优先遍历,若解空间树的节点满足约束条件(和限界函数),则继续搜索,否则进行减枝。回溯法最重要的是构造解空间树,以此撰写回溯程序。
回溯法三要素:
解向量,约束条件和限界函数,解空间树(结点表示状态,边表示选择)
回溯法的一般过程:
void backtrack(int depth,vector<vector> & path)
//depth为搜索的深度,从根结点开始。二维向量path记录解向量,即从根结点到叶子节点的路径
{
if (depth > n) //递归出口。搜索到叶子结点,输出一个可行解。
path.push_back(x[]);
else
{
for (int j = 下界;j = 上界; j++)//用j枚举i所有可能的路径。
{
x[depth] = j; //产生一个可能的解分量。
第一种写法:满足约束条件和限界函数的情况即不冲突
if(constraint(depth) && bound(depth))
backtrack(depth + 1, path); //若满足约束条件和限界函数,递归下一层
(可能的回溯操作)
第二种写法:不满足约束条件和限界函数的情况即冲突
if(冲突)
{flag=flase;break;}
if(flag) backtrack(depth + 1, path);//不冲突时,递归下一层
}
}
}
#include <iostream>
; using namespace std;
#include<vector>
void dns(int k, int n, int depth, vector<vector<int>>&v, vector<int> &color, const int a[20][20])
{
if (depth==n)//递归出口
{
v.push_back(color); color.resize(n, 0);//输出着色方法,并对向量color复原
}
else
{
for (int j = 1; j <= k; j++)//枚举各种着色可能
{
bool flag = true;
color[depth] = j;
for (int i = 0; i <depth; i++)//检查该点与邻近点的着色是否冲突
if (a[depth][i] == 1 && color[i] == j)
{
flag = false; break;
}
if(flag) dns(k, n, depth + 1, v, color, a);//不冲突时,递归下一层
}
}
}
int main()
{
int hang;
// 测试用例 int a[5][5] = { {0,1,1,0,0},{1,0,1,1,1},{1,1,0,0,1},{0,1,0,0,1},{0,1,1,1,0} };
cout << "请输入图的节点数:";
cin >> hang;
int a[20][20];
cout << "请输入图的邻接矩阵:" << endl;
for (int i = 0; i < hang; i++)
for (int j = 0; j < hang; j++)
cin >> a[i][j];
vector<int> color;//color[i]表示第i个节点着第color种颜色
color.resize(hang,0);//初始化
vector<vector<int>>v;
int k = 2;//图着色至少2种颜色
dns(k, hang, 0, v, color, a);
while (!v.size())
{
k++;
dns(k, hang, 0, v, color, a);
}
cout << "该图最少用" << k << "种颜色着色" << endl << "有" << v.size() << "种涂色法" << endl;
for (auto it = v.begin(); it != v.end(); it++)
{
for(auto z=(*it).begin();z!=(*it).end();z++)
cout<<*z<<" ";
cout<<endl;
}
}
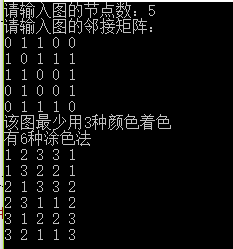
测试用例:

测试用例输出结果: