博客

什么是拓扑排序？

此处采用百度百科的解释：

执行步骤：

循环执行以下两步，直到不存在入度为0的顶点为止。

(1) 选择一个入度为0的顶点并输出之；

(2) 从网中删除此顶点及所有出边。

循环结束后，若输出的顶点数小于网中的顶点数，则输出“有环路”信息，否则输出的顶点序列就是一种拓扑序列。

一个简单的实例(过程)：

实现：

利用邻接矩阵表示两者的关系。

将上述示例中的图用邻接矩阵表示：

参考代码：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<queue> 
#include<vector>
using namespace std;
const int maxV = 1000;
const int INF = 100000000;

//拓扑排序
// DAG图：有向无环图 
//inDegree[v]表示v的入度是什么 
int n, m, inDegree[maxV];
vector<int> G[maxV];

bool topologicalSort(){
	
	int count = 0;//顶点个数
	queue<int> q; 
	
	//入度为0的进队列 
	for(int i = 0; i < n; i ++){	
		if(inDegree[i] == 0){
			q.push(i);
		}
	}
	while(!q.empty()){
		int u = q.front();
		//cout << u << " ";//可输出 
		q.pop();
		
		for(int i = 0; i < G[u].size(); i ++){
			int v = G[u][i];// u的后继顶点
			
			//和他相关的后继节点都对-- 
			inDegree[v] --;
			if(inDegree[v] == 0) q.push(v); 
		}
		
		G[u].clear(); //每次清空
		count ++; 
	}
			
	return count == n ? true : false; 
}


int main(){
	
	while(cin >> n){
		//邻接矩阵表示关系 
		vector<vector<int>> relations(n, vector<int>(n, 0));
		for(int i = 0; i < n; ++ i){
			for(int j = 0; j < n; ++ j){
				//从i到j的关系 从i指向j 
				cin >> relations[i][j]; 
				
				if(relations[i][j] == 1){
					G[i].push_back(j); 
					inDegree[j] ++;
				}
			}
		} 
		cout << topologicalSort() << endl;	
	} 
	
	return 0; 
} 

测试截图：

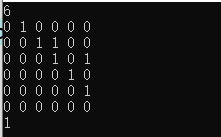
leetcode中相关习题：

课程表 II

题目描述：现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。 例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回一种就可以了。如果不可能完成所有课程，返回一个空数组。

参考代码：

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        //1.BFS - queue
        //2.DFS - dfs() - visited[]
        //[a, b] 先学完b才可以学a b->a
        unordered_map<int, vector<int>> graph;//映射为图
        vector<int> indegree(numCourses, 0);
       
       int i = 0;
        for(i = 0; i < prerequisites.size(); i ++){
            graph[prerequisites[i][1]].push_back(prerequisites[i][0]);
            indegree[prerequisites[i][0]] ++;//记录入度
        }

        queue<int> q;
        for(i = 0; i < numCourses; i ++){// 0-n-1
            if(indegree[i] == 0) q.push(i);
        }

        vector<int> res;
        while(!q.empty()){
            int front = q.front();
            q.pop();

            res.push_back(front);
            for(i = 0; i < graph[front].size(); i ++){
                int now = graph[front][i];
                indegree[now] --;
                if(indegree[now] == 0) q.push(now);
            }
        }

        if(res.size() < numCourses) res.clear(); //无拓扑排序结果
        return res;
    }
};

以上就是这篇的主要内容，如有疑问或错误之处，请您指出，谢谢！