作者:teeyohuang
本文系原创,供交流学习使用,转载请注明出处,谢谢
声明:此系列博文根据斯坦福CS229课程,吴恩达主讲 所写,为本人自学笔记,写成博客分享出来
博文中部分图片和公式都来源于CS229官方notes。
CS229的视频和讲义均为互联网公开资源
Lecture8
主要内容如下:
·Kernels (核方法)
·Soft Margin(软间隔) –非线性可分的情况
·SMO algorithm
1.Kernels (核方法)
上一节课的最后我们已经推出了一些有用的结论:


这是我们探讨核方法的出发点
假设我们现在有一个输入属性(input attribute)x,有时候我们会将这个x给映射到一组新的集合上去,
比如如下例子,采用特征映射 (feature mapping) φ:
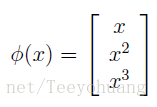
我们把得到的这组新的量称为 输入特征(input features)
这样,如果我们想通过新的这组input features求解svm,只需要把之前讲过程中的所有出现了x的地方用φ(x)代替就ok了。
假设现在有内积
<x,z>
,则直接将其写为<φ(x) φ(z)>,我们将这个内积定义为一个核:
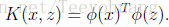
一般φ(x)的维度都比较高,直接把φ(x)计算并表示出来显得很复杂,但是计算K(x,z)的复杂度一般要低一些,所以往往不必把φ(x)或者φ(z)显示地表达出来。举个例子说明:

下面看另一个核的例子,
如果φ(x)和φ(z)很接近,那么它们的内积就比较大,也就是说期望核的值K(x,z)比较大;如果它们彼此远离,甚至接近正交,那么它们的内积K(x,z)就会比较小,甚至于接近0。
所以我们可以认为核函数K(x,z)能够在一定程度上测定φ(x)和φ(z)的相似性,或者说x和z的相似性。比如下面这个核函数:

如果
x和z接近的话,值就会接近1;反之x和z相隔很远的话,值会接近0
。
那么我们能够在SVM中用到这个核吗?对于这个具体的例子来说,是可以的,这个核其实被称作Gaussian kernel,实际上对应了一个无限维度的映射函数φ。
但是问题来了,我们该
如何判定一个核函数
K
是否合法(有效)呢?
换句话说,我们能否
找到一个合适的
特征映射函数φ
,
使得
K = <φ(x) φ(z)>
对于当前问题的所有x和z都成立。如果根本都找不到一个合适的φ,说明我们无法从x,z构建出这样一个核函数!
实际上有一个结论,给出了函数K是合法的核的充分必要条件
①先来看必要条件
:
假设现在已知K是一个合法的核函数,对应着一个映射函数φ。
现在,考虑包含了m个点的有限集合(不一定非得是训练集) :
,
使得有一个m x m大小的矩阵K,的元素
Kij = K(x(i), x(j)).
这样的一个矩阵
K
被称为
kernel matrix
(核矩阵)
根据基本的数学知识,内积是可交换的,即
<φ(x) φ(z)> = <φ(z) φ(x)>
,
那么显然,对于刚刚那个核矩阵来说,
Kij = Kji
,
也就是说,
K
矩阵是对称矩阵
接下来,对于任意一个向量
z
,φ
k
(x)
是φ
(x)
中的第
k
个值,有如下推导:

从而得知K是一个positive semi-definite matrix —半正定矩阵。
则
必要条件
就为:如果K是一个合法的核函数,那么K函数对应的
K
矩阵就一定是一个
对称的半正定矩阵
。
实际上,这个
条件也是充分条件
,使得
K
是一个合法的核,称为
Mercer kernel
Mercer定理:任何的半正定函数都可以作为核函数。
给出了判定一个核函数是否是合法的标准。
其实总结起来,核方法的作用就是将特征映射到高维空间中去,所以也不局限于SVM中应用,
2.L1 norm soft Margin
在这之前,我们探讨的都是数据线性可分的情况,但是有时候数据是线性不可分的,如下图左图;
或者即便线性可分,但是分割函数并不理想,如下图右图:
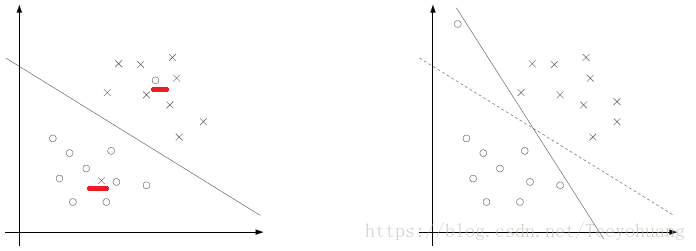
所以我们就希望算法对这些极端值不敏感,这样就相当于尽量忽略这些极端值,那么剩下的大部分样本就还是线性可分的。
这些极端值无法满足间隔大于等于1的
约束条件
,所以我们对每个样本点再引入一个松弛变量
ξi
≥
0,使得间隔函数加上松弛变量大于等于1.即约束条件变为:

如果某个样本的函数间隔为 1- ξ
i
的话,我们就应该对损失函数增加一个代价:Cξ
i
。 所以最终的损失函数和约束条件如下:
损失函数中多出来的那部分代价想表达的意思是,最小化这部分代价意味着
更少的样本点
,会
需要加上这个
ξ
才能满足函数间隔大于1;试想,
如果
ξ
是一个极大的数的话,那么光凭借
ξ
的值就能满足约束条件了
,那么我们的函数间隔那部分就没有意义了,所以
希望
ξ
这部分代价能取的尽量的小
。C是一个常数,用来控制这部分的权重而已。
如果说我们之前讲的
线性
可分
的数据
的SVM可以被称为
线性
可分
支持向量机
,那么这里对于
线性不可分的数据,但是却近似线性可分
(比如只有极个别的极端值,)的数据,是能够通过软间隔来学习出线性SVM的,可称为
线性支持向量
机。
同样可以写出它的拉格朗日乘式,
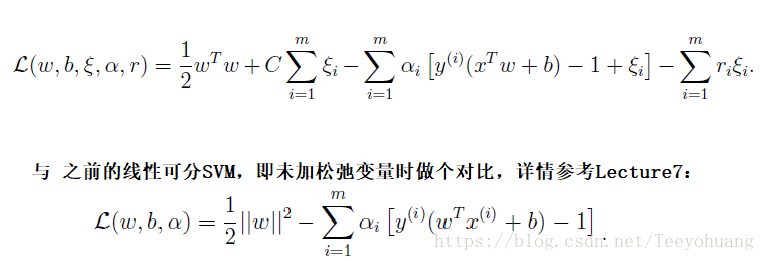
具体的详细的推导过程我们就不细讲了,参考Lecture7中的详细推导步骤,这里直接给出对偶结果:
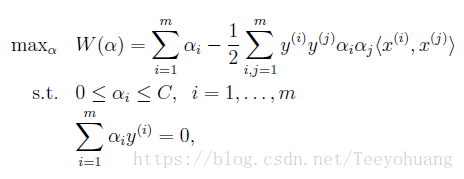
我们会发现这个对偶问题与Lecture7中解决线性可分SVM中的对偶问题相比,只是对于αi的约束多了一个:αi≤C,
但要主要的是对于b的计算公式需要进行修改。同时KKT dual-complementarity(对偶互补条件)为:
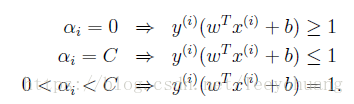
要想解决这个对偶问题,就会讲到下面的SMO算法
3.SMO algorithm (sequential minimal optimization)顺序最小优化算法
坐标上升法:
先来看一个无约束优化问题:
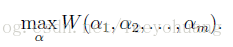
W是参数α的函数,现在我们先不考虑有关SVM的任何东西,这就是个单纯的优化问题。我们在前面已经就讲过两种优化方法,梯度上升和牛顿方法,可以用来解决这个问题,但是这次提出一个新的方法:坐标上升法:

可以看到在算法的最内层循环中,我们固定除了αi的其余所有参数,然后对于参数αi最大化整个函数,最内层按照α1、α2、α3…的循环(也可以选择其他更复杂的顺序)。
这里朋友们要注意的是 在算argmax,而不是max,
就是说我们这里求的不是函数的最大值,而是使函数能取得最大值的参数αi的最大值
坐标上升算法是一个相当高效的算法,执行过程见下图:
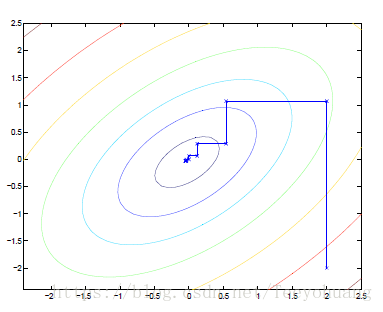
图中的椭圆是我们想要优化的一个二次函数的轮廓。坐标上升算法的初始点为(2,-2),图中描点的路径是到达全局最大的路径。在每一步,坐标上升算法平行地沿着一个轴运动,一次仅有一个变量被优化。简单的说,就是固定x求能使得函数值最大的y,再固定y求能使函数值最大的x,如此循环……
了解了坐标上升算法之后,我们再来看之前提到的对偶问题:
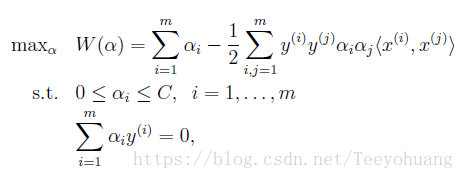
对于这个对偶问题,我们确实需要求解一系列的αi,那么我们能直接使用坐标上升算法吗?
答案是不行!
因为约束条件中的第二个条件所限制,以α1为例:如果想固定除了α1以外的所有其它α是不能做到的,因为:

即因为
它们的和是一个固定值,如果固定了其余m-1个参数,那么这一个参数也就被固定了。
所以不能直接使用坐标上升算法。
但是,如果我们同时更新两个参数,固定其余m-2个参数可否呢?这样其实就可以了,因为这两个参数自己有自己调整的内部空间。
这就是SMO算法,过程如下:

SMO是一个高效的算法的关键原因是,
更新αi,αj可以被高效地计算
。
可以简单的推导一下:
现在固定除了α1,α2 之外的其余m-2个α,那么就会得到一个新的约束:
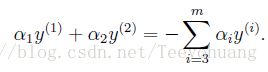
因为右侧被固定,就是一个常数而已,改写为:
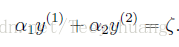
画出函数图:
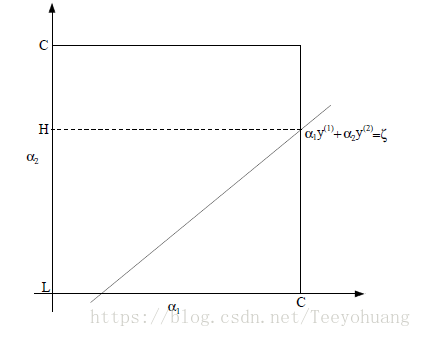
因为约束条件中0≤αi≤C,所以α1和α2必须存在于[0,C]×[0,C]的方形区域内,直线为:α1y(1)+α2y(2) = ζ,
与框形区域有两个交点。
可知,固定α1时, α2需要落在[L,H]范围内,否则无法满足条件,此图中L=0.
我们完全可以将α1写作α2的函数:α1 = (ζ − α2y(2)) y(1).
那么优化问题可以被写为:
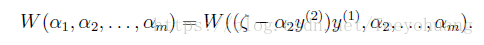
Y因为其他参数都被固定,所以这可以视为仅仅是一个关于α2的二次函数,如果我们先暂时不考虑α2的限制范围,直接通过梯度方法求得最小值,那么设这个值为:α2-new-unclipped
然后再对其进行截断操作:
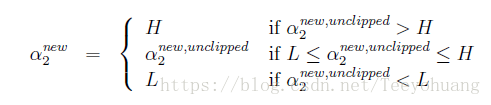
之后再把这个值代入优化函数中去求α1即可
我靠这篇博文终于写完了,眼睛都要瞎了……