谈谈常见的迭代优化方法

如果学习机器学习算法，你会发现，其实机器学习的过程大概就是定义一个模型的目标函数

$J(\theta)$
，然后通过优化算法从数据中求取

$J(\theta)$
取得极值时对应模型参数

$\theta$
的过程，而学习到的参数就对应于机器学习到的知识。不管学习到的是好的还是无用的，我们知道这其中的动力引擎就是优化算法。在很多开源软件包中都有自己实现的一套优化算法包，比如stanford-nlp，希望通过本篇简要介绍之后，对于开源软件包里面的优化方法不至于太陌生。本文主要介绍三种方法，分别是梯度下降，共轭梯度法(Conjugate Gradient Method)和近似牛顿法(Quasi-Newton)。具体在stanford-nlp中都有对应的实现，由于前两种方法都涉及到梯度的概念，我们首先从介绍梯度开始。

梯度(Gradient)

什么是梯度，记忆中好像和高数里面的微积分有关。好，只要您也有这么一点印象就好办了，我们知道微积分的鼻祖是牛顿，人家是经典力学的奠基人，那么我们先来看看一道简单的物理问题：

一个小球在一个平面运动，沿着x轴的位移随时间的变化为：

$S_x=20-t^2$
，沿着y轴的位移随时间的变化为：

$S_y=10+2t^2$
，现在求在

$t_0$
时刻小球的速度

$v$
？

大家都是为高考奋战过的人，这样的小题应该是送分题吧。牛老师告诉我们，只要通过求各个方向的分速度，然后再合成就可以求解得出。好，现在我们知道各个方向的位移关于时间的变化规律，我们来求各个方向的速度。如何求速度呢，牛老师说位移的变化率就是速度，那么我们来求在

$t_0$
时刻的变化率：

v x (t 0) = l i m Δ t - > 0 ( 20 - ( t 0 + Δ t ) 2 ) - ( 20 - t 2 0 ) Δ t = - 2 t 0

$v_x(t_0)=lim_{\Delta t->0}\frac{(20-(t_0+\Delta t)^2)-(20-t_0^2)}{\Delta t}=-2t_0$

v y (t 0) = l i m Δ t - > 0 ( 10 + 2 ( t 0 + Δ t ) 2 ) - ( 10 + 2 t 2 0 ) Δ t = 4 t 0

$v_y(t_0)=lim_{\Delta t->0}\frac{(10+2(t_0+\Delta t)^2)-(10+2t_0^2)}{\Delta t}=4t_0$
，那么此时的合成速度

$v$
:

v = v x + v y = [- 2 t 0, 4 t 0]

$v=v_x+v_y=[-2t_0,4t_0]$
，此时的速度方向就是总位移变化最大的方向。搬到数学中，对于一个位移函数

$S(x,y)$
，它各个维度的变化率就是其对应的偏导数

\partial S ( x , y ) \partial x, \partial S ( x , y ) \partial y

$\frac{\partial S(x,y)}{\partial x},\frac{\partial S(x,y)}{\partial y}$
，两者组合起来的向量就是该函数的梯度，所代表的含义上面已经说过，其方向代表函数变化最大的方向，模为变化率的大小。如果我们分别沿着

$x,y$
两个维度做微小的变化

$\Delta x,\Delta y$
,那么位移总体的变化将如下：

Δ S (x, y) \approx \partial S ( x , y ) \partial x * Δ x + \partial S ( x , y ) \partial y * Δ y

$\Delta S(x,y)\approx\frac{\partial S(x,y)}{\partial x}* \Delta x + \frac{\partial S(x,y)}{\partial y} * \Delta y$
现在我们知道如何求取函数的梯度，而且如何利用梯度求取函数微小变化量了。

梯度下降法

做机器学习(监督学习)的时候，一般情况是这样的，有

$N$
条训练数据

$(X^{(i)},y^{(i)})$
，我们的模型会根据

$X$
预测出对应的

$y$
，也就是：

y (i) 预 测 = f (X (i); θ)

$y^{(i)}_{预测}=f(X^{(i)};\theta)$
其中

$\theta = [\theta _1,\theta_2,\theta_3,...,\theta_n]$
是模型的参数。通常我们希望预测值和真实值是一致的，所以会引出一个惩罚函数:

c o s t (y (i) 预 测, y (i) 真 实)

$cost(y^{(i)}_{预测},y^{(i)}_{真实})$
而目标函数则是：

J (θ) = \sum i = 0 N c o s t (y (i) 真 实, y (i) 预 测) = \sum i = 0 N c o s t (y (i) 真 实, f (X (i); θ))

$J(\theta)=\sum^N_{i=0}cost(y^{(i)}_{真实},y^{(i)}_{预测})=\sum^N_{i=0}cost(y^{(i)}_{真实},f(X^{(i)};\theta))$
，我们目的是解决下面的优化问题:

a r g m i n θ J (θ)

$argmin_{\theta} J(\theta)$
，一般一组

$\theta$
和

$N$
条数据会对应一个

$J(\theta)$
，也就是

$N$
维平面上的一个点，那么不同

$\theta$
就可以得到一个

$N$
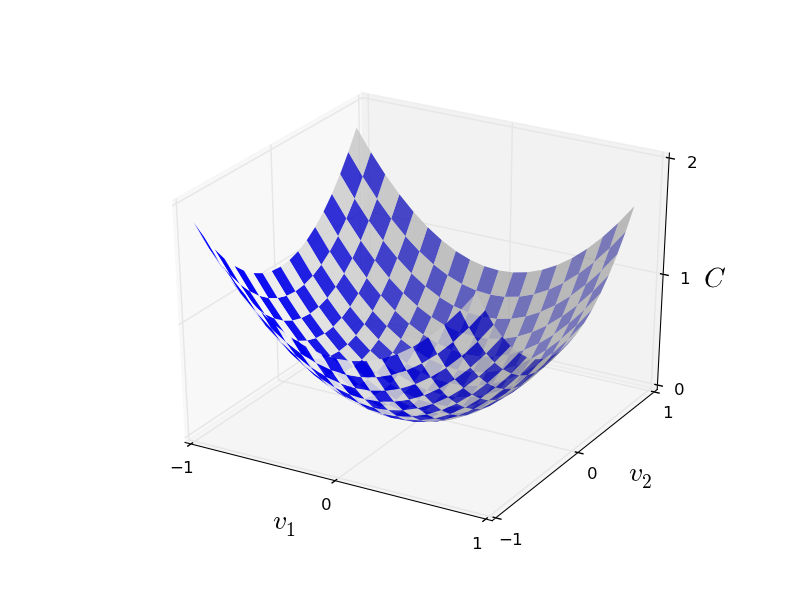
维的超平面(hyper plane)。特殊的假如

$N=3$
，我们可能的超平面就如下图所示：

如何找到最优的

$\theta$
呢？一个想法是这样的：我们随机在超平面上取一个点，对应我们

$\theta$
的初始值，然后每次改变一点

$\Delta \theta$
，使

$J(\theta)$
也改变

$\Delta J(\theta)$
，只要能保证

$\Delta J < 0$
就一直更新

$\theta$
直到

$J(\theta)$
不再减少为止。具体如下：

随机初始化

$\theta$
对于每一个

$\theta_i$
选择合适的

$\Delta \theta_i$
，使得

$J(\theta+\Delta \theta)-J(\theta)<0$
,如果找不到这样的

$\Delta \theta$
，则结束算法
对于每一个

$\theta_i$
进行更新：

$\theta_i = \theta_i + \Delta \theta_i$
，回到第2步。

想法挺好的，那么如何找到所谓合适的

$\Delta \theta$
呢？根据上一节中我们知道：

Δ J (θ) \approx \sum i \partial J ( θ ) \partial θ i * Δ θ i

$\Delta J(\theta) \approx \sum_i \frac{\partial J(\theta)}{\partial \theta_i}*\Delta \theta_i$
,要如何保证

$\Delta J(\theta) <0$
呢？我们知道，两个非0数相乘，要保证大于0，只要两个数一样即可，如果我们要保证

$\Delta J(\theta)>0$
，只要另每一个

$\theta_i＝\frac{\partial J(\theta)}{\partial \theta_i}$
即可，此时

Δ J (θ) \approx \sum i \partial J ( θ ) \partial θ i * \partial J ( θ ) \partial θ i > 0

$\Delta J(\theta) \approx \sum_i \frac{\partial J(\theta)}{\partial \theta_i}*\frac{\partial J(\theta)}{\partial \theta_i} > 0$
，有人疑问了，我们目标可是要使

$\Delta J(\theta)<0$
，上面的做法刚好相反啊！反应快的人可能马上想到了，我们只需另每一个

$\theta_i＝-\frac{\partial J(\theta)}{\partial \theta_i}$
不就好了，而这样的求取向量

$\theta$
各个维度相对于

$J(\theta)$
的偏导数实际上就是求取

$J(\theta)$
的梯度！回忆上一节梯度的含义，表示

$J(\theta)$
变化最大的方向，想象一个球在上面的图中上方滚下来，而我们的做法是使他沿着最陡的方向滚。不错，我们找到了上述算法所说的合适的

$\Delta \theta$
了！其实上述的算法就是我们本文的主角——梯度下降法(gradient descent)，完整算法如下：

随机初始化

$\theta$
求取

$\theta$
的梯度

$\nabla \theta$
，也就是对于每个

$\theta_i$
求取其偏导数

$\frac{\partial J(\theta)}{\partial \theta_i}$
，并更新

$\theta_i = \theta_i - \eta * \frac{\partial J(\theta)}{\partial \theta_i}(\eta > 0并足够小)$
判断

$\nabla \theta$
是否为0或者足够小，是就输出此时的

$\theta$
，否则返回第2步

上述算法的第二步中多了一个未曾介绍的

$\eta$
，这是步伐大小，因为求取每一个维度的偏导，只是求取了该维度上的变化率，具体要变化多大就由

$\eta$
控制了，

$\eta$
的选取更多考验的是你的工程能力，取太大是不可行的，这样导致算法无法收敛，取太小则会导致训练时间太长，有兴趣的可参考

An overview of gradient descent optimization algorithms

这篇文章中对

$\eta$
选取的一些算法。如何计算

$\frac{\partial J(\theta)}{\partial \theta_i}$
呢？根据定义，可如下计算：

\partial J ( θ ) \partial θ i = \sum i = 0 N \partial c o s t ( y ( i ) 真 实 , f ( X ( i ) ; θ ) ) \partial θ i

$\frac{\partial J(\theta)}{\partial \theta_i}=\sum^N_{i=0}\frac{\partial cost(y^{(i)}_{真实},f(X^{(i)};\theta))}{\partial \theta_i}$
，由于每次计算梯度都需要用到所有

$N$
条训练数据，所以这种算法也叫批量梯度下降法(Batch gradient descent)。在实际情况中，有时候我们的训练数据数以亿计，那么这样的批量计算消耗太大了，所以我们可以近似计算梯度，也就是只取

$M(M<<N)$
条数据来计算梯度，这种做法是现在最流行的训练神经网络算法，叫mini-batch gradient descent。最极端的，我们只用一条训练数据来计算梯度，此时这样的算法叫做随机梯度下降法(stochastic gradient descent)，适合数据是流式数据，一次只给一条训练数据。

共轭梯度法

上一节中，我们介绍了一般的梯度下降法，这是很多开源软件包里面都会提供的一种算法。现在我们来看看另外一种软件包也经常见到算法——共轭梯度法(Conjugate Gradient Method)，Jonathan在94年的时候写过《

An Introduction to the Conjugate Gradient Method Without the Agonizing Pain

》详细而直观地介绍了CG，确实文如其名。这里我只是简要介绍CG到底是一个什么样的东西，具体还需阅读原文，强烈推荐啊！

最陡下降法(Steepest Descent)

上一节中，我们介绍了如何反复利用

$\theta_i = \theta_i - \eta * \frac{\partial J(\theta)}{\partial \theta_i}$
求得最优的

$\theta$
，但是我们说选取

$\eta$
是一个艺术活，这里介绍一种

$\eta$
的选取方式。首先明确一点，我们希望每次改变

$\theta$
，使得

$J(\theta)$
越来越小。在梯度确定的情况下，其实

$\Delta J(\theta)$
是关于

$\eta$
的一个函数：

ϕ (η) = J (θ - η * \nabla θ) - J (θ) = Δ J (θ)

$\phi(\eta)=J(\theta-\eta*\nabla \theta) - J(\theta)=\Delta J(\theta)$
，既然我们想让

$J(\theta)$
减小，那么干脆每一步都使得

$|\Delta J(\theta)|$
最大好了，理论上我们可以通过求导求极值，令：

ϕ' (η) = 0

$\phi'(\eta)=0$
求得此时的

$\eta$
，这样每次改变

$J(\theta)$
是最大的，而实际操作中，我们一般采用line search的技术来求取

$\eta$
，也就是固定此时的梯度

$\nabla \theta$
，也就是固定方向，尝试不同的

$\eta$
值，使得

J (θ - η * \nabla θ)

$J(\theta-\eta*\nabla \theta)$
近似最小即可。这样固定方向的搜索和直线搜索没太大区别，也是名字的由来。表面看来，最陡梯度下降法应该是最优的啊，不但方向上是最陡的，而且走的步伐也是”最优”的，但是实际应用该方法的地方并不多，因为步伐的局部最优并不代表全局最优，导致其实际表现收敛速度比较慢(这却是优化算法的致命弱点！)。如果

$J(\theta)$
是一个二次函数也就是

$J(\theta)=\theta^TA\theta+b^T\theta+c$
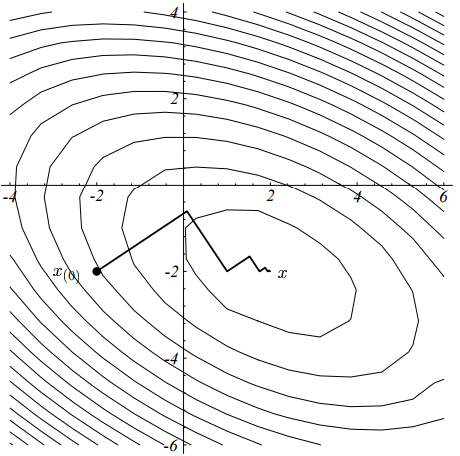
，通过运行算法，我们可以得到一个如下的轨迹：

最陡下降法轨迹

我们可以发现，每一次走的步伐和上一次都是垂直的(事实上是可以证明的，在前面我推荐的文中有详细的证明:-))，这样必然有很多步伐是平行的，造成同一个方向要走好几次。研究最优化的人野心就来了，既然同一个方向要走好几次，能不能有什么办法，使得同一个方向只走一次就可以了呢？

共轭梯度法

Cornelius，Magnus和Eduard经过研究之后，便设计了这样的方法——共轭梯度法。
这里写图片描述

具体详细的原理还是强烈推荐《

An Introduction to the Conjugate Gradient Method Without the Agonizing Pain

》一文，这里我只是利用文章中的思路进行简要介绍。

何谓共轭(Conjugate)

查看维基的介绍，共轭梯度法(CG)最早的提出是为了解决大规模线性方程求解，比如下面形式:

A x = b

$Ax=b$
，其中

$A$
是方形对称半正定的。如果

$A$
越大并且越稀疏，导致其他线性方程求解不可行的时候，CG方法就更奏效。

我们已经了解梯度为何物，现在就差修饰词共轭(Conjugate)了，那么何为共轭(conjugate)呢？对于两个非零向量

$d_{(i)},d_{(j)}$
,如果满足

d T (i) A d (j) = 0

$d_{(i)}^TAd_{(j)}=0$
我们就称

$d_{(i)},d_{(j)}$
是关于

$A$
共轭的，也就是说其实共轭不共轭是相对于

$A$
而言。我们知道，如果两个向量正交，他们的内积为0，所以如果两个向量关于

$A$
是共轭的，我们也可以称这两个向量关于

$A$
是正交的，也就是

$A-orthogonal$
。

共轭梯度法求解线性方程组

那么求解上面线性方程组的时候，假如我们已经找到

$n$
个两两共轭的方向

$\{d_{(i)}\}$
，如果将这些方向作为基，也就可以将

$Ax=b$
的解表示为

$d_{(i)}$
的线性组合：

x * = \sum i n α i d (i)

$x_*=\sum_i^n \alpha_i d_{(i)}$
如果左右分别乘上

$A$
:

A x * = \sum i n α i A d (i)

$Ax_*=\sum_i^n \alpha_i A d_{(i)}$

b = \sum i n α i A d (i)

$b=\sum_i^n \alpha_i A d_{(i)}$

d T (k) b = \sum i n α i d T (k) A d (i) = α k d T (k) A d (k)

$d_{(k)}^Tb=\sum_i^n \alpha_i d^T_{(k)} A d_{(i)}\\=\alpha_k d^T_{(k)} A d_{(k)}$
，也就是

$\alpha_k=\frac{d_{(k)}^T b}{d^T_{(k)} A d_{(k)}}$
。现在问题就只在于如何找到这些神奇的共轭方向了，神奇之处在于这些共轭方向可以利用迭代方式求取，可以一次只求一个这样的方向向量

$d_{(k)}$
，这也是该算法的核心之处。如果令

$r_k=b-Ax_k$
,那么

d (k + 1) = r k + β k d (k)

$d_{(k+1)}=r_k+\beta_k d_{(k)}$
其中

$\beta_k = \frac{r^T_{k+1} r_{k+1}}{r_k^Tr_k}$

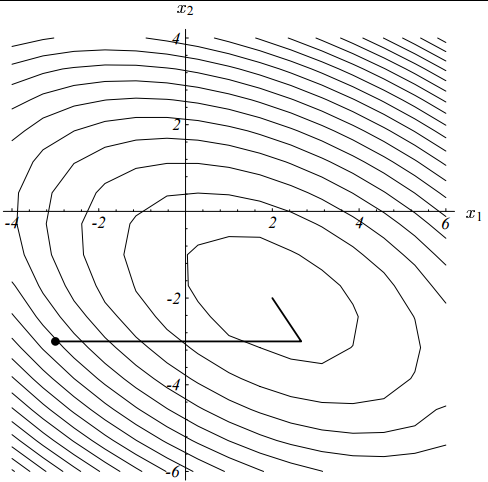
上一小节中利用Steepest Method的优化问题如果利用CG就变成了如下：

这里写图片描述

二维的情况下，可以保证只走两步就达到收敛(严格的证明请参靠推荐的论文)！

非线性共轭梯度法

机器学习算法中，我们碰到的大部分问题都是非线性的，上面我们只是讲解了线性共轭梯度法，那么它可以解决非线性优化问题吗？很遗憾，不行，但是经过修改，可以利用共轭梯度法求取局部最优解，下面展示非线性共轭梯度法的大致轮廓,对于一个非线性目标函数

$J(\theta)$

随机初始化

$\theta_0$
，并令

$r_0=d_{(0)} = -J'(\theta_0)$
对于k = 0,1,2….
- 利用line search找出使得
  
  $J(\theta_k+\alpha_i d_{(k)})$
  足够小的
  
  $\alpha_k$
- $\theta_{k+1} = \theta_k + \alpha_k d_{(k)}$
- $r_{k+1} = -J'(\theta_{k+1})$
- $d_{(k+1)} = r_{k+1} + \beta_{k+1} d_{(k)}$

这里又出现了

$\beta_i$
,对于

$\beta$
的研究，著名的方法有:Hestenes-Stiefel方法、Fletcher-Reeves方法、Polak-Ribiére-Polyak 方法和Dai-Yuan方法，分别对应于：

β H S k = ( r k + 1 - r k ) T r k + 1 d T ( k ) ( r k + 1 - r k )

$\beta_k^{HS}=\frac{(r_{k+1}-r_k)^Tr_{k+1}}{d_{(k)}^T(r_{k+1}-r_k)}$

β F R k = | | r k + 1 | | 2 | | r k | | 2

$\beta_k^{FR}=\frac{||r_{k+1}||^2}{||r_k||^2}$

β P R P k = ( r k + 1 - r k ) T r k + 1 | | r k | | 2

$\beta_k^{PRP}=\frac{(r_{k+1}-r_k)^Tr_{k+1}}{||r_k||^2}$

β D Y k = | | r k + 1 | | 2 d T ( k ) ( r k + 1 - r k )

$\beta_k^{DY}=\frac{||r_{k+1}||^2}{d_{(k)}^T(r_{k+1}-r_k)}$

需要注意的是，非线性共轭梯度法并不能像解决线性系统那样，保证

$n$
步内收敛，一般我们迭代很多次直到

$||r_{k}|| < \epsilon ||r_0||$
。

像CG这样高效的方法，一般都有现成的工具库可以使用，只要我们提供目标函数的一次导函数和初始值，CG就能帮我们找到我们想要的了！再次推荐《

An Introduction to the Conjugate Gradient Method Without the Agonizing Pain

》一文。

近似牛顿法(Quasi-Newton)

上一节中介绍开源软件包常见的方法Conjugate Gradient Method，这一节我们来介绍另一个常见的方法——Quasi-Newton Method。

牛顿法(Newton Method)

我们高中的时候数学课本上介绍过牛顿求根法，具体的做法是：对于一个连续可导的函数

$f(x)$
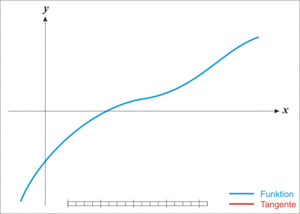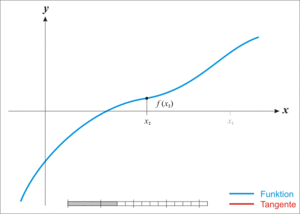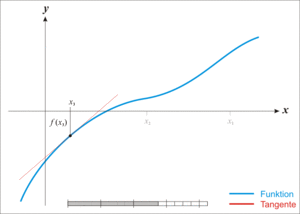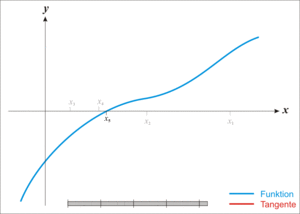
，我们如何求取它的零点呢，看看维基百科是如何展示牛老师的方法:

如图所示，我们首先随机初始化

$x_0$
，然后每一次利用曲线在当前

$x_i$
的切线与横轴的交点作为下一个尝试点

$x_{i+1}$
，具体更新公式：

x i + 1 = x i - f ( x i ) f ' ( x i )

$x_{i+1}=x_i-\frac{f(x_i)}{f'(x_i)}$
，直到

$f(x_i)\approx0$
为止。牛老师告诉我们一个求取函数0点的方法，那么对于我们本篇的优化问题有什么帮助呢，我们知道，函数的极值在于导数为0的点取得，那么我们可以利用牛老师的方法求得导数为0的点啊。我们目的是求取

$J'(\theta)=0$
对应的

$\theta$
，那么我们可以依样画葫芦（假设

$J(\theta)$
是二阶可导的）按照如下更新：

While

J

′

(

θ

)

没有足够小：
- $\theta = \theta - \frac{J'(\theta)}{J''(\theta)}$

其中

$J''(\theta)$
是一个矩阵：

J'' (θ) = ⎧ ⎩ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ \partial J ( θ ) \partial θ 0 \partial θ 0 . . . \partial J ( θ ) \partial θ n \partial θ 0 \partial J ( θ ) \partial θ 0 \partial θ 1 . . . \partial J ( θ ) \partial θ n \partial θ 1 . . . . . . . . . \partial J ( θ ) \partial θ 0 \partial θ n \partial J ( θ ) \partial θ n \partial θ n ⎫ ⎭ ⎬ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ = H (2)

$J''(\theta)= \left\{ \begin{matrix} \frac{\partial J(\theta)}{\partial \theta_0\partial \theta_0} & \frac{\partial J(\theta)}{\partial \theta_0\partial \theta_1}&...& \frac{\partial J(\theta)}{\partial \theta_0\partial \theta_n} \\ . & . & . \\ . & . & . \\ . & . & . \\ \frac{\partial J(\theta)}{\partial \theta_n\partial \theta_0} & \frac{\partial J(\theta)}{\partial \theta_n\partial \theta_1}&...& \frac{\partial J(\theta)}{\partial \theta_n\partial \theta_n} \end{matrix} \right\} \tag{2}=H$
也就是大名鼎鼎的Hession矩阵。而牛顿法更新中:

θ = θ - J ' ( θ ) J '' ( θ ) = θ - η H - 1 J' (θ) (实 际 应 用 我 们 会 加 入 步 伐 η ， 可 以 用 l i n e s e a r c h 求 得 最 优 的 η)

$\theta = \theta - \frac{J'(\theta)}{J''(\theta)} = \theta - \eta H^{-1}J'(\theta)\\(实际应用我们会加入步伐\eta，可以用line search求得最优的\eta)$
涉及到Hession矩阵的求逆过程，对于一些参数比较多的模型，这个矩阵将非常巨大，计算也极其耗时，所以这就为什么实际项目中很少直接使用牛老师的方法。不过之前我们介绍的方法都只利用了一阶信息，牛老师的方法启发了利用二阶信息优化方式。

L-BFGS算法

上一小节中，我们介绍了牛顿法，并且指出它一个严重的缺陷，就是计算Hession矩阵和求逆有时候内存和时间都不允许。那么有什么办法可以近似利用牛顿法呢，也就是有没有Quasi-Newton Method呢？答案是有的，BFGS算法就是一个比较著名的近似牛顿法，对于BFGS的介绍，另外有一篇博客有很好的介绍，具体参阅《

Numerical Optimization: Understanding L-BFGS

》，也是非常直观简洁的介绍，还附有Java和Scala源码，非常值得学习。

BFGS算法核心在于他利用迭代的方式(具体方式请参考上面推荐的博文，文章不长，可读性很强)近似求解Hession矩阵的逆，使得求解Hession矩阵的逆变得不再是神话。而迭代的过程步骤是无限制的，这也会导致内存不足问题，所以工程上利用有限步骤来近似BFGS求解Hession的逆，就成了Limit-BFGS算法。与很多算法一样，这个算法名字是取4位发明者的名字首字母命名的，所以单看名字是没有意义的:-)。

这里写图片描述

以上是几位大佬的尊荣。利用Quasi-Newton法，在处理数据规模不大的算法模型，比如Logistic Regression，可以很快收敛，是所有优化算法包不可或缺的利器。

参考引用

原文链接：https://blog.csdn.net/aws3217150/article/details/50548177

梯度(Gradient)

梯度下降法

共轭梯度法

最陡下降法(Steepest Descent)

共轭梯度法

何谓共轭(Conjugate)

共轭梯度法求解线性方程组

非线性共轭梯度法

近似牛顿法(Quasi-Newton)

牛顿法(Newton Method)

L-BFGS算法

参考引用

你可能也喜欢