递推例题
在这之前,我们先了解一下递推的基本原理
举一个生活中的例子:
你要上楼梯(每层楼有20个台阶,1楼没有架空)
你想上到3楼,你要从1-2-3这个顺序爬到3楼
你从1到2,再从2到3
换句话说,你走到第2楼是在你身处第1楼的情况下才能有的,走到第3楼是你在你身处第2楼的情况下才有的
这样就可以得到一个十分简单的递推式:f(i)代表你走到第i楼所走的台阶数,一共要走n楼
f(i)=f(i-1)+20, 1≤i≤n
一般的递推包含3个部分
1、分析出递推式
2、确定变量范围
3、初始化
———————————————————————————————
题目描述
用1 x 1和2 x 2的地砖不重叠地铺满N x 3的地板,共有多少种方案?
输入
一个数字N<=1000
输出
所求的答案mod 12345.
样例输入
2
样例输出
3
看完题,第一想法是递归
但是N的取值范围忒大了,时间复杂度估一下就知道会爆
这时候递推的好处就体现出来了,通常的递归都差不多在O(N²)、O(NlgN)、O(N)左右的时间内求出答案,这正是我们当前所想要的
先找一下规律:
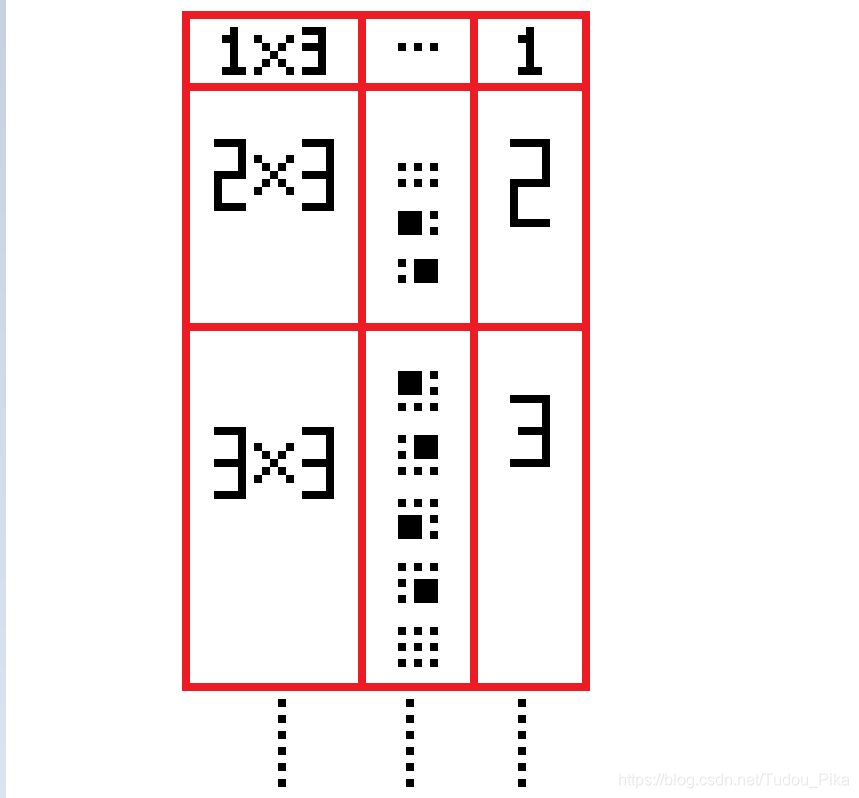
这有点类似于小学奥数的通项公式
定义递推式:F(i)=在i * 3的地板中按照题目要求所有的铺法数量
F(i)=2 × F(i-2)+F(i-1)
现在就完成了递推的第一个部分(递推式)
递推式有两种求法:
1是找规律(容易错
2是直接想
像这一题,i×3的地板中的铺法
要么是把上一行和这一行变成一个2×2的加两个1×1的
而且2×2地砖是有两种摆法,所以当前i列的摆法要先加上两个i-2时的铺法:
f[i]+=f[i-2]*2;
如图:
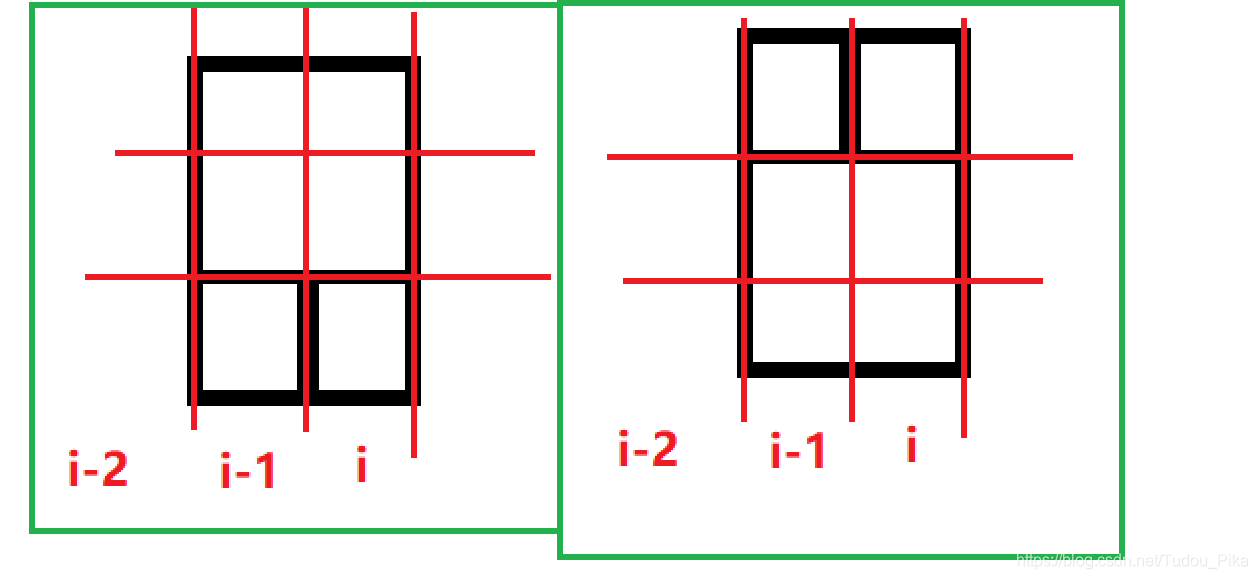
或者是在当前列只铺三个1×1的地砖:
而且只有一种铺法,所以当前i列的摆法要再加上两个i-1时的铺法:
f[i]+=f[i-1];
如图:

然后把i的范围求出来:
很显然,i至少要是3
3≤i≤n
第二个部分完成
然后是初始化,套用草稿上的东西完成初始化,f[1]=1,f[2]=3;
f[1]=1;
f[2]=3;
for(int i=3;i<=n;i++)
f[i]=f[i-2]*2+f[i-1];
原题上还要取模,自行修改
接下来还有几题:
题目描述
从原点出发,一步只能向右走、向上走或向左走。恰好走N步且不经过已走的点共有多少种走法?
输入
一个数字N<=1000
输出
一个数表示所求答案mod 12345.
样例输入
2
样例输出
7
定义递推式 (i,j)等于第i步是从j方向过来的方案数
j的取值:0 =从下面上来的 1=从右边往左边来的 2=从左边往右边来的
例如:f[3][0]代表第三步是从下面上来的方案数
通过画图发现,无论怎样走,不可能从中途走重复路,例如:

要想从中间走重复路,只能往下,所以不存在上图中走回头路的情况
那走回头路的情况只有:
先往左走,再往右走
以及
先往右走,再往左走
所以到达每一步的方式是有限的
f(当前第i步,从下面上来的情况)=上一步中上、左、右三种可能的方案之和
f(当前第i步,从左边过来的情况)=上一步中上、左两种可能的方案之和 (如果上一步是往右,这一步就会走回头路)
f(当前第i步,从右边过来的情况)=上一步中上、右两种可能的方案之和(跟左边过来的的同理)
由此推出方程
(0代表从下面上来,1代表从左边过来,2代表从右边过来
f[i][0]=f[i-1][0]+f[i-1][1]+f[i-1][2];
f[i][1]+=f[i-1][0]+f[i-1][1];
f[i][2]+=f[i-1][0]+f[i-1][2];
1≤i≤n
时间复杂度 O(N)
f[1][0]=1;
f[1][1]=1;
f[1][2]=1;
for(int i=2;i<=n;i++)
{
f[i][0]+=(f[i-1][0]+f[i-1][1]+f[i-1][2])%12345;
f[i][1]+=(f[i-1][0]+f[i-1][1])%12345;
f[i][2]+=(f[i-1][0]+f[i-1][2])%12345;
}
printf("%d",(f[n][0]+f[n][1]+f[n][2])%12345);
第三题:
题目描述
在所有的N位数中,有多少个数中有偶数个数字3?
输入
一个整数N<=1000
输出
输出一个数表示答案mod 12345.
样例输入
2
样例输出
73
这题按照上面的两种方法可以自己想想递推式
f[1]=9;
f[2]=73;
f[3]=674;
h[3]=900;
for(int i=4;i<=n;i++)
{
h[i]=h[i-1]*10;
f[i]=f[i-1]*9+(h[i-1]-f[i-1]);
f[i]%=12345;
h[i]%=12345;
}
第四题:
题目描述
圆周上有N个点。连接任意多条(可能是0条)不相交的弦(共用端点也算相交)共有多少种方案?
输入
读入一个数N。1<=N<=1000。
输出
输出这个答案mod 12345的值。
样例输入
4
样例输出
9
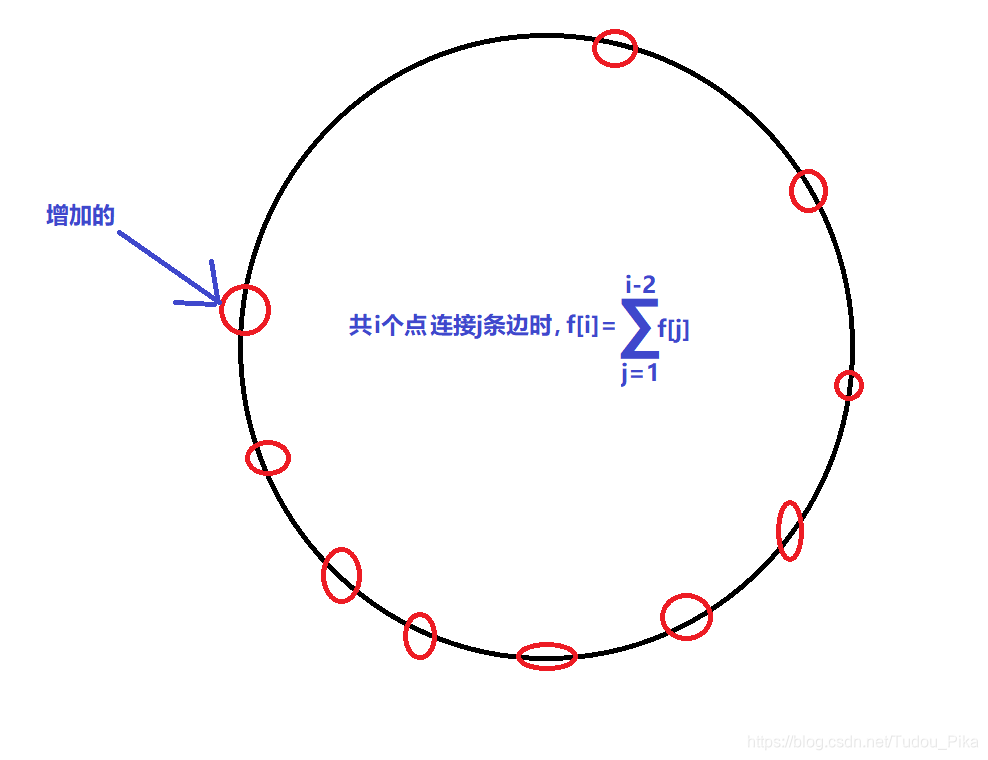
f[0]=1;
f[1]=1;
for(int i=2;i<=n;i++)
{
f[i]=f[i-1];
int uck=0;
for(int j=i-2;j>=0;j--)
{
f[i]+=f[j]*f[uck];
f[i]%=12345;
uck++;
}
}
第五题:
题目描述
在网格中取一个N x 1的矩形,并把它当作一个无向图。这个图有2(N+1)个顶点,有3(N-1)+4条边。这个图有多少个生成树?答案 mod 12345 后输出。
输入
样例输入:1
输出
答案 mod 12345 后输出。
样例输入
1
样例输出
4

f[0]=1;
f[1]=4;
for(int i=2;i<=n;i++)
{
f[i]=f[i-1]*4-f[i-2]+12345;
f[i]%=12345;
}
可以发现,递推的题目大部分解法都是三个步骤:递推式->变量范围->初始化
以后大部分的题目不会单独递推,递推会变为一个步骤
所以对比繁琐亢长的递归,递推显然简洁