//文章在本人资源一栏有完整word文档(免费)或者到四足控制/机器人学笔记(一) – 择 守的文章 – 知乎
https://zhuanlan.zhihu.com/p/595764705
此地方观看完整版,由于csdn的发布文章总会出现一些奇奇怪怪的问题,只能出此下策。//
概述
首先声明,笔者只是一位大二在读学生,并不是专业人士,自学的机器人学,写这个首先是为了让实验室以后打马术赛的师弟师妹们在学习机器人学和运动控制算法的时候,可以借鉴一下往届师兄的想法,其次是为了在写这个博客的时候顺路把自己的对应知识巩固一下,毕竟是自学的,还是需要时不时强化记忆,如果有什么错误请一定一定指正,在此谢过各位。
思维导图
十月份的时候觉得自己学东西比较没有方向,所以在结合自己学习机器人学的经历,写代码时查的资料还有赛中赛后和哈尔滨工业大学深圳校区,南方科技大学的几位老哥交流之后,初步完成了这份比较简陋的四足机器人软件层的思维导图

四足机器人的控制算法和机械臂机械爪,还有一些双足六足机器人的控制算法一般都叫运动控制算法,运动控制算法在学习的时候需要结合大量基础知识,从运动学动力学到静力学,这就要求我们在开始写算法之前一定要有充足的知识储备,所以不能想着直接不学前面的学科基础直接跳到算法层面进行学习,一旦这样做,可以预见,要么看不懂代码中的各种矩阵,要么电机疯转,无法实现目标效果。
机器人位姿表示和坐标变换
机器人位姿表示和坐标变换是学习机器人学的入门部分,也是运动控制算法中位置控制的实现基础。在学习机器人运动学之前我们应该先学会一些基础知识。
自由度(Degree of Freedom/DOF)
自由度在机器人学里是一个比较常见的基础名词,一个物体的自由度通俗来讲就是你去定义它的位置需要的元素个数,比如一辆汽车在平面移动,你只需要两个坐标x,y就可以在平面定位他的位置,再用一个角度去确定他的方向就可以定位,这是就说他有三自由度,同理,在天空中飞行的飞机就有三个移动自由度和三个转动自由度,一共是六个自由度。
机器人位姿的数学表示
在以往许多代码中,目标点往往是以二维平面的形式表现出来,但是在机器人学中我们会在笛卡尔坐标系下的三维空间进行表述,这就要求一个物体至少需要三个元素来表示,我们以笛卡尔坐标系下空间直角坐标系为参考,机器人的每一个关节(joint)都会有一个对应的坐标,一般坐标原点处于刚体的质心上。

在确定好质心之后建立一个空间直角坐标系,并且找到准备相对移动的参考坐标系,然后我们会以向量的形式来描述物体的状态,如下图

质心的移动和转动
移动
移动其实很简单,例如上图,要将原点移动到p点,因为在笛卡尔坐标系上沿着坐标轴移动是不会再其他方向产生分量的,所以只要分别沿着x,y,z轴移动相对距离就好。
旋转
旋转比起移动来说就稍微复杂一点,首先我们看一下旋转矩阵的样子

最前面的R是旋转矩阵Rotation matrix中的开头字母,左边的AB是元素从A坐标系移动到B坐标系上,第一行中间的x,y,z代表的是一个3×1的矩阵,分别代表了B坐标系上元素p的x,y,z在A坐标系上的投影,说明白一点就是将在B坐标系上的元素p的x,y,z三个向量分别投影到A向量中,每一个向量投影到A坐标系上就是一个3×1的矩阵,也就是第二行的第一列,第二列和第三列,XB说明这个是在B坐标系上的P元素的x向量,后面的·XA,·YA,·ZA分别是把X向量投影到A坐标系上对应的X,Y,Z轴上,如下图
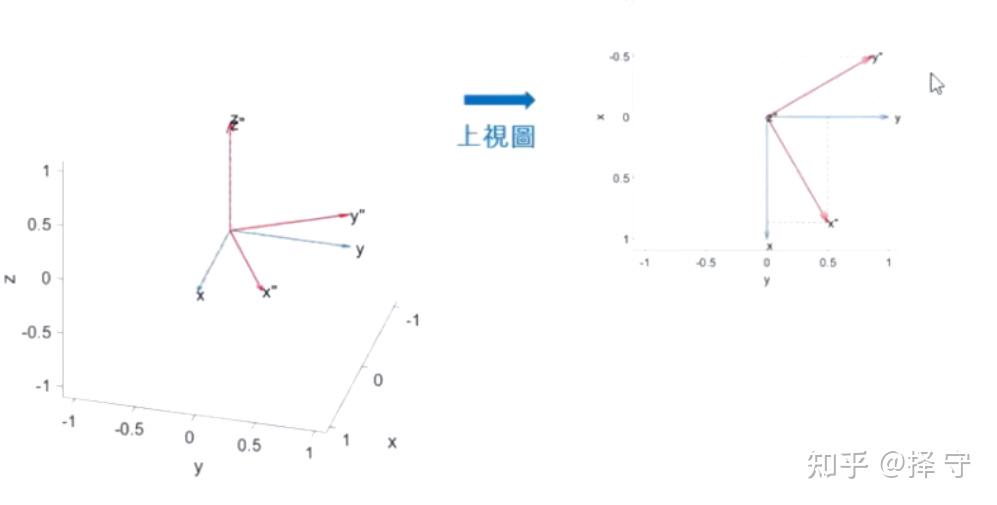
两者运算结束后如下图

旋转矩阵
旋转矩阵有几个特性,我们一般需要知道两个
特性一:
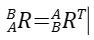

由图可知,从A坐标系向B坐标系进行转变的旋转矩阵R1的转置就等于从B坐标系向A坐标系转变的旋转矩阵R2



对于绕着不同的轴转动theta度,有着不同的旋转矩阵,如下图所示,表示旋转矩阵的字母R的下标代表绕A坐标系的Z轴进行转动。
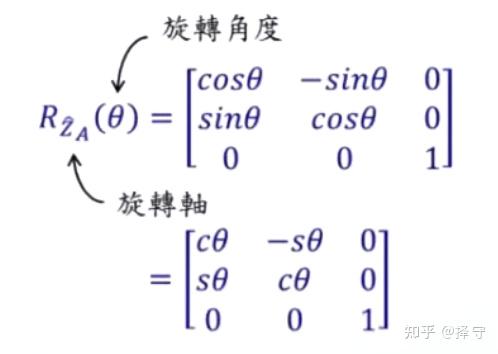
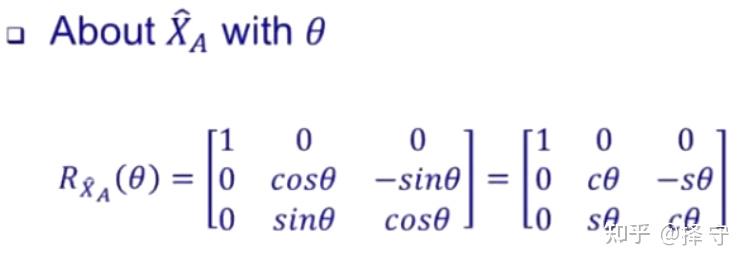
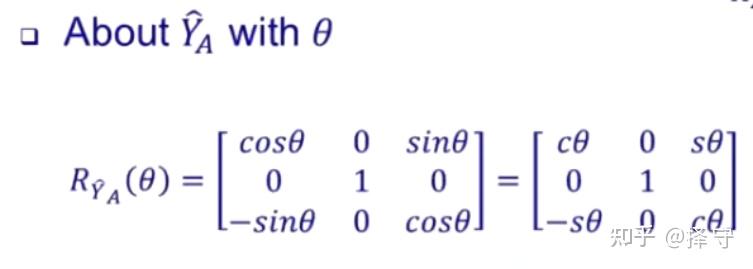
机器人姿态的其他表示方法
Fixed Angles/RPY角(固定坐标系)
在进行运算之前,我们应该先搞懂一个问题,如何去理解绕x,y,z轴旋转呢,以一艘船为例子,垂直船甲板的平面的轴为x轴,船前进的方向为z轴,用右手定则,与x,z轴互相垂直的方向定为y轴,我们一般以垂直船的右侧面的轴为y轴,定义绕Z轴的运动为Roll(翻滚),绕Y轴的运动叫Pitch(俯仰),绕X轴的运动叫Yaw(偏航/左右转向)。由此可得各轴在机器人关节运动时实际控制的作用。
正解运算:目标坐标系j和世界坐标系/参考坐标系i原点坐标相同,目标坐标系j首先绕轴转角,再绕轴转角,最后绕轴绕角,表现在算式上就是从右往左乘,而RPY角的特点是固定坐标系,因为在运算过程中参考坐标系,也就是绕的轴所在的坐标系一直是一个参考坐标系。

算式如下(从右往左乘,先转x再转y最后转z):
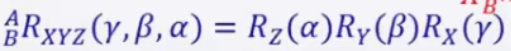

特别注意:旋转矩阵不满足交换律,一定要按顺序进行计算。
Euler Angles(欧拉角)
欧拉角和RPY角在旋转轴的设定上没有区别,主要区别在于欧拉角的正逆解运算的顺序和原理。
和RPY角的固定坐标系运算不同,欧拉角的特别之处在于他的参考坐标系是实时变换的,每次进行变换完之后,变换完的坐标系就是新的参考坐标系。欧拉角有两种表示方法,ZYX角和ZXZ角,在这里只解释ZYX角,ZXZ角不做具体讲解。
ZYX角正解运算:首先目标坐标系i1与参考坐标系j重合,先绕j的Z轴转动alfa角,此时目标坐标系转变为i2,再以i2为参考坐标系,绕i2的Y轴转动beta角,目标坐标系转变为i3,最后以i3为参考坐标系,绕i3的X轴转动theta角。在使用欧拉角的时候就没有必要像RPY角一样从右往左乘,这里是从左往右乘,但是算式和RPY角是一样的,依然是下式,只是运算方向发生了改变。这也从侧面说明了坐标系绕定轴旋转和绕动轴旋转具有等效性,转变过程如下:

算式如下(从左往右乘,先算z再算y最后算x):


再次特别注意:旋转矩阵不满足交换律,一定要按顺序进行计算。
Homogeneous Transformation matrix(齐次变换矩阵)

结尾
第一次由于时间关系,先整理到这里,下次就开始讲机器人运动学了。机器人的位姿表示和坐标变换对初学者来说也是一个比较难理解的地方(个人认为),我的笔记只是讲出了我在学这些的时候心里的想法,不敢说我的想法一定对,但我认为大部分还是可以借鉴的,另外舍去了一些内容没讲,毕竟这是一个笔记,我不可能全部都讲全,只能说讲一些我认为比较有用的东西来帮助大家学习机器人学,另外,由于CSDN的公式编辑器的问题,有些下标我可能标的比较乱,和书上的不一样,一般情况下表示坐标系的i和j做下标上标都是在字母左侧的,可能有些标到右侧,特此说明。
最后,谢谢观看,有错误请指正。