LeetCode刷题——搜索（python语言）

一、搜索

搜索简单来说分为查找和遍历。

查找分为有序查找（二分查找）和无序查找（顺序查找，二叉搜索树）。

顺序查找：一个挨一个找，从头找到尾，属于暴力算法。效率低

二叉搜素树，保证一个条件就是左子树的值小于根节点的值小于右子树的值。这样中序遍历获得从小到大的元素

二分查找：前提是已经排好序，可以将待查找元素和中间位置元素比较，然后修改左右指针。

遍历分为深度优先搜索（DFS）和广度优先搜索（BFS）。

深度优先搜索（DFS）主要的遍历思想是栈（stack），即后进先出原则，那么需要先将一个结点即他的孩子结点遍历完毕，才会继续遍历兄弟结点。一个通俗易懂的例子就是：张三和李四在一个饭店排队，饭店只允许一家人吃饭。张三在前，李四在后，张三买到饭后，张三和他的家人就可以吃到饭，而李四和他的家人要继续等到张三和他的家人吃完以后才可以吃饭，

广度优先搜索（BFS）主要遍历思想是队列（queue），即先进先出原则，那么需要将一个结点和他的兄弟结点遍历完毕，才会继续遍历孩子结点。一个通俗易懂的例子是，张三和李四在一个饭店排队，饭店只允许外送，一份饭只够一个人吃。所以张三和李四一次都做好饭，张三拿走饭，李四拿走饭。而他的加入只能在后面继续等。

二、刷题

2.1 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9

输出: 4

解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2

输出: -1

解释: 2 不存在 nums 中因此返回 -1

提示：

你可以假设 nums 中的所有元素是不重复的。

n 将在 [1, 10000]之间。

nums 的每个元素都将在 [-9999, 9999]之间。


题解

：由于数组已经排好顺序，所以采用二分法查找元素。根据中间元素的值判断方向。

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        n = len(nums)
        left,right=0,n-1
        while(left<=right):
            mid = (left+right)//2 
            if(nums[mid]==target):
                return mid 
            elif(nums[mid]<target):
                left = mid + 1 
            else:
                right = mid - 1 
        return -1

2.2 搜索旋转排序数组

整数数组 nums 按升序排列，数组中的值 互不相同 。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], …, nums[n-1], nums[0], nums[1], …, nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0

输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3

输出：-1

示例 3：

输入：nums = [1], target = 0

输出：-1

提示：

1 <= nums.length <= 5000

-10^4 <= nums[i] <= 10^4

nums 中的每个值都 独一无二

题目数据保证 nums 在预先未知的某个下标上进行了旋转

-10^4 <= target <= 10^4

进阶：你可以设计一个时间复杂度为 O(log n) 的解决方案吗？


解法1

：还是二分法查找。但是这个数组已经部分乱序了，但是我们可以利用一半的排好序的数组进行查找。首先判断中间元素是否是待查找的元素。然后分左半部分有序和右半部分有序的情况，根据target值进行指针的移动。




⋆

\star






⋆





该代码超时

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        n = len(nums)
        left,right = 0,n-1
        while(left<=right):
            mid = (left+right)//2 
            if(nums[mid]==target):
                return mid
            if(nums[mid]>=nums[left]): #左半部分有序
                if(target>nums[mid]): 
                    left = mid + 1 
                else:
                    if(target==nums[left]):
                        return left
                    else:
                        if(target>nums[left]):
                            right = mid - 1 
                        else:
                            left = mid + 1
            else: #右半部分有序
                if(target<nums[mid]):
                    rigth = mid - 1 
                else:
                    if(target==nums[right]):
                        return right
                    else:
                        if(target<nums[right]):
                            left = mid + 1 
                        else:
                            right = mid - 1
        return -1 

解法2

：这个方法与上面相似，唯一不同的是写法有所区别。采用了python的多个不等号的写法。分别保证target在区间存在。

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        # 二分查找
        n=len(nums)
        left=0
        right=n
        while left<right:
            mid=(left+right)//2
            if nums[mid]==target:
                return mid
            elif nums[0]<=nums[mid]:#[left,mid]是有序数组
                if nums[mid]>target>=nums[0]:# >=nums[0]保证target存在
                    right=mid
                else:
                    left=mid+1
            elif nums[0]>nums[mid]:#[mid,right]是有序数组
                if nums[mid]<target<=nums[n-1]:#<=nums[n-1]保证target存在
                    left=mid+1
                else:
                    right=mid
        return -1

2.3 二叉树的中序遍历

给定一个二叉树的根节点 root ，返回它的 中序 遍历。

示例 1：

输入：root = [1,null,2,3]

输出：[1,3,2]

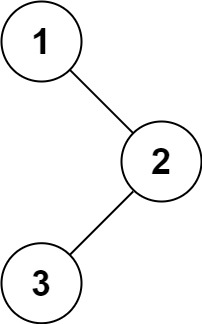
示例 2：

输入：root = []

输出：[]

示例 3：

输入：root = [1]

输出：[1]

示例 4：

输入：root = [1,2]

输出：[2,1]

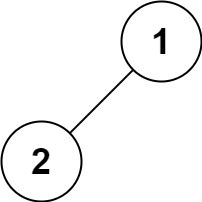
示例 5：

输入：root = [1,null,2]

输出：[1,2]

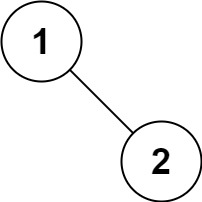
提示：

树中节点数目在范围 [0, 100] 内

-100 <= Node.val <= 100

进阶: 递归算法很简单，你可以通过迭代算法完成吗？


解法

：二叉树的中序遍历比较简单，采用DFS应用递归，使用左根右遍历

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def inorderTraversal(self, root: Optional[TreeNode]) -> List[int]:
        self.ans = []
        def dfs(root):
            if(not root):
                return 
            dfs(root.left)
            self.ans.append(root.val)
            dfs(root.right)
        dfs(root)
        
        return self.ans

2.4 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]

输出：true

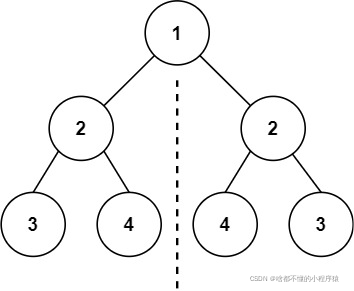
示例 2：

输入：root = [1,2,2,null,3,null,3]

输出：false

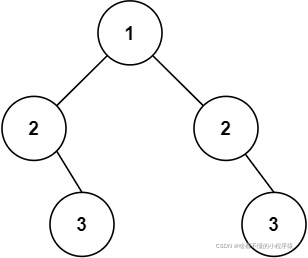
提示：

树中节点数目在范围 [1, 1000] 内

-100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？


解法

：这个问题主要采用BFS（广度优先搜索）解，主要核心思想是队列的应用，即先进先出。对于每一层，加入元素（空元素加入None）。然后对数组倒置比较。其中应用到了python的copy方法和reverse方法。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def isSymmetric(self, root: TreeNode) -> bool:
        nodes = [root]
        while(nodes):
            ans_num = []
            ans_node = []
            for root in nodes:
                if(not root):
                    continue
                if(root.left):
                    ans_node.append(root.left)
                    ans_num.append(root.left.val)
                else:
                    ans_num.append(None)
                if(root.right):
                    ans_node.append(root.right)
                    ans_num.append(root.right.val)
                else:
                    ans_num.append(None)
            new_num = ans_num.copy()
            new_num.reverse()
            if(ans_num!=new_num):
                return False 
            nodes = ans_node
        return True
            

2.5 二叉搜索树中第K小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例 1：

输入：root = [3,1,4,null,2], k = 1

输出：1

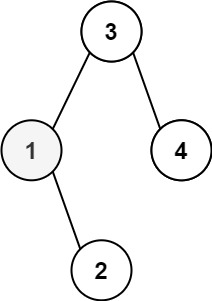
示例 2：

输入：root = [5,3,6,2,4,null,null,1], k = 3

输出：3

提示:

树中的节点数为 n 。

1 <= k <= n <= 104

0 <= Node.val <= 104

进阶：如果二叉搜索树经常被修改（插入/删除操作）并且你需要频繁地查找第 k 小的值，你将如何优化算法？

**解法：**二叉搜索树根据二叉树的中序排列可以输出二叉树元素由小到大的列表。然后输出k-1号元素的值即可。

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, val=0, left=None, right=None):
#         self.val = val
#         self.left = left
#         self.right = right
class Solution:
    def kthSmallest(self, root: Optional[TreeNode], k: int) -> int:
        nums = []
        def DFS(root):
            if(not root):
                return 
            DFS(root.left)
            nums.append(root.val)
            DFS(root.right)
        DFS(root)
        return nums[k-1]