前言碎碎念

我是大菜鸟，做了一次蓝桥杯模拟赛，发现自己几乎没有对的。下文将从一个菜鸟的角度写题解+总结。

考完之后模拟赛的题目界面已经进不去了，题意我只能大概描述一下了。我的代码是参考蓝桥云课官方解析写的，但是已经进不去题目界面了，没有再次提交，如有纰漏，请大家指出~

数A

题意：

结果填空题，给出一个只含A、B的字符矩阵，要求计算出这个矩阵中A的个数是多少。

思路：

枚举+遍历字符串问题。读入字符串，然后从左到右遍历，遇到A就计数1次，最后输出计数即可~

关于读入字符串的方法：

我做的时候是

scanf("%s",A)

，就是只读入1行字符串。但是由于题目给的数据是有很多行那种，每行末尾都有

\n

，因此我不能直接copy数据，还得自己人工预处理一下，把一个矩阵字符删成只有1行字符，保存在txt文件中，然后重定向输入

freopen("F:\\蓝桥杯\\模拟赛\\A_data.txt","r",stdin);

来读入。因为数据的行数也不少，人工预处理还是花时间的。所以这个法子不行。

一个比较好的做法是，每次读入1行字符串，多读几次，就可以省去人工预处理的时间。

答案：318

代码：

这是那种可以直接copy数据的写法。

#include<iostream>
#include<string>
using namespace std;
int main()
{
	string s;
	const int n=25; // 数据有25行
	int ans = 0;
	for(int i=0; i<n; i++) {
		cin>>s;
		for(int j=0; j<s.length(); j++) {
			if(s[j]=='A') ans++;
		}
	}
	cout<<ans;
	return 0;
}

最2数字

题意：

计算1（包含）到2021（包含），有多少个数字的某个数位包含2。

思路：

结果填空题。我感觉这是蓝桥杯出现频率很高的考点了，找一群数字的某个数位是否包含某个数。

我的做法是，用C++的 to_string函数+find函数来写。写得挺快，就是一旦题目稍微变一下，要

统计所有数字中2出现的次数

，就不会了。

官方做法是，用

/

和

%

两种运算符来整数分解，由于这个数字的范围最多不会超过4位，可以默认所有数都是4位的，来进行分解。即使可能会有前导0，也不影响对2的判断。

我感觉两种解法都不错，所以都写一下了。

答案：564

代码：

to_string + find。

#include<cstdio>
#include<string>
using namespace std;
int judge(int x);
int main()
{
	int ret = 0;
	for(int i=1; i<=2021; ++i) {
		ret += judge(i);
	}
	printf("%d",ret);
	return 0;
}
int judge(int x) {
	string s = to_string(x);
	if(s.find('2')==string::npos) return 0;
	return 1;
}

整数分解。

#include<iostream>
using namespace std;
int main()
{
	int ans = 0;
	for(int i=1; i<=2021; i++) {
		int a = i%10; //个位数
		int b = i/10%10; //十位数
		int c = i/100%10; //百位数
		int d = i/1000%10; //千位数 
		if(a==2 || b==2 || c==2 || d==2) ans++;
	}
	cout<<ans;
	return 0;
}

数字操作

题意：

有一个数字2021，每次可以将这个数+1、-1、或者除以2（只有这个数是偶数时，才可以除以2）。求2021

最少经过多少次操作

才能变成1。

思路：

我完全想错了！！我以为不断执行遇到奇数-1，偶数除以2的操作，求出的操作次数一定是最少的。

虽然现在我还是不知道为什么这样做，求出的操作次数居然不是最少的，有知道的大佬可以教教我！

合理的做法是，用数字作为结点，三种变换规则做边，来建立图，然后

用BFS求从2021到1的最短路径

。所以题干的设问“最少经过多少次操作”转变为最短路径问题。orz 卑微了，这个转化是我万万没想到的。

BFS的实现就是模板题，借助于C++ 的queue。（救命，我脑抽了，修改代码的时候，居然写的是stack）

答案：14

代码：

#include<iostream>
#include<queue>
using namespace std;
queue<int> q;
bool vis[3000] = {false};
int dis[3000] = {0}; // dis[]存该结点距离2021的操作次数 
int main()
{
	q.push(2021);
	vis[2021] = true;
	dis[2021] = 0;
	while(!q.empty()) {
		int x = q.front();
		if(x == 1) break;  
		q.pop();
		if(vis[x+1] == false) {
			q.push(x+1);
			vis[x+1] = true;
			dis[x+1] = dis[x]+1;
		}
		if(vis[x-1] == false) {
			q.push(x-1);
			vis[x-1] = true;
			dis[x-1] = dis[x]+1;
		}
		if(x%2==0 && vis[x/2] == false) {
			q.push(x/2);
			vis[x/2] = true;
			dis[x/2] = dis[x]+1;
		}
	}
	cout << dis[1];
	return 0;
}

注意：

• q应该是永远不会empty的，因为它可以一直+1，无穷无尽。所以循环真正的结束条件，还是x==1时，break。

螺旋矩阵

题意：

思路：

结果填空题。我当时是用excel一行一行去填的，居然居然居然答案是错的！！！被自己蠢到了！我只想说

论检查的重要性

。我肉眼根本没看出来excel哪里做错了，最后跟程序的输出结果对比才看出来的。我不能太相信我自己的手工劳动orz。

官方的做法，是改编了一下走迷宫的模板，从起点开始，按照一定的方向去走，一旦遇到被走过的格子，就旋转90°继续走。需要注意的是，这里不必开一个

vis[]

数组来记录格子是不是被访问过。直接初始化二维数组都为0，并且填上去的数都是正整数，因此格子里的数不是0，就代表已经访问过了。

答案：819

代码：

#include<iostream>
using namespace std;
int maze[50][50] = {0};
int X[4] = {1,0,-1,0};
int Y[4] = {0,1,0,-1};
bool judge(int xx, int yy) {
	if(xx<1 || xx>30 || yy<1 || yy>30) return false;
	if(maze[yy][xx]!=0) return false;
	return true;
}
int main()
{
	int x=1, y=1, k=0;
	maze[y][x] = 1;
	for(int i=2; i<=30*30; i++) {
		int newX = x+X[k];
		int newY = y+Y[k];
		if(judge(newX,newY)) {
			maze[newY][newX] = i;
			x = newX;
			y = newY;
		}
		else {
			k = (k+1)%4;
			newX = x+X[k];
			newY = y+Y[k];
			maze[newY][newX] = i;
			x = newX;
			y = newY;
		}
	} 
	// test
	// test部分可以打印出来看看结果，最后提交记得注释掉~
	for(int i=1; i<=30; i++) {
		for(int j=1; j<=30; j++) {
			printf("%d ",maze[i][j]);
		}
		printf("\n");
	}
	cout<<maze[20][20];
	return 0;
}

最大深度

题意：





思路：

结果填空题。我写的时候，一看这是一道二叉树的题就很慌张，

因为虽然我学过数据结构但是树的知识全忘了

（就是菜）。

刚刚去百度了一下，还是没找到那个已知结点数，求平衡二叉树深度的公式，知道的大佬可以指点一下我orz

但是这道题只是披了一个二叉树的壳子而已，用到的二叉树特性都已经在题干中说明。就算不记得公式也可以用

递归

来做。二叉树的深度等于

max(左子树深度，右子树深度)+1

。因此，记

f(n)

为结点数为n的平衡二叉树的深度，则有递推式

f(n)=f(n/2)+1

，这里涉及到n为奇数和偶数的情况，稍微举个例子就能理解。递归终止条件是

f(1)=0

，即根结点的深度为0。

答案：10

代码：


递归版。（其实用递推也可以，主要是要想到这个方法上面来）

#include<iostream>
using namespace std;
int f(int x) {
	if(x==1) return 0;
	else return f(x/2)+1;
}
int main()
{
	cout<<f(2021);
	return 0;
}

和尚挑水

题意：

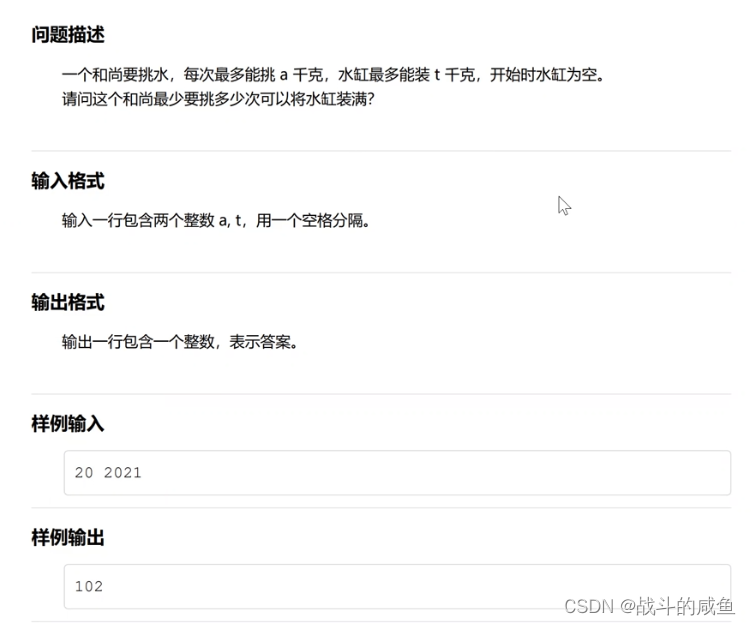
思路：

我大为震撼，这个题我都能写错！！！！我直接用

t/a+1

的。我甚至还多余地考虑了

a>t

的情况，把它单拎出来判断，其实没必要的。

正确的思路就是先

t/a

，至于是否+1，要看

t%a

的情况。

做蓝桥杯千万不能只过了样例就交，一定要自己多测试几组数据！！！

代码：

#include<iostream>
using namespace std;
int main()
{
	int a,t,ans;
	cin>>a>>t;
	ans = t/a;
	if(t%a != 0) ans++;
	cout<<ans;
}

千分读入

题意：

思路：

是简单的字符串处理题目。读入字符串，去遍历它，遇到

,

就跳过，其他则输出。

如果题目反过来，问的是输入一串数字，要求转化成从个位开始，每3位加一个逗号的格式输出。我也写了一下。

代码：


本题的代码。

#include<cstdio>
#include<cstring>
using namespace std;
int main()
{
	char A[30];
	scanf("%s",A);
	int len = strlen(A);
	for(int i=0; i<len; i++) {
		if(A[i]!=',') printf("%c",A[i]);
	}
	return 0;
}

如果题目要求反过来的话。主要是注意下标问题。

#include<iostream>
#include<string>
using namespace std;
int main()
{
	string s;
	cin>>s;
	for(int i=0; i<s.size(); i++) {
		if(s.size()-i>3 && (s.size()-i)%3==0) {
			cout<<",";
		}
		cout<<s[i];
	}
	return 0;
}

插头

题意：

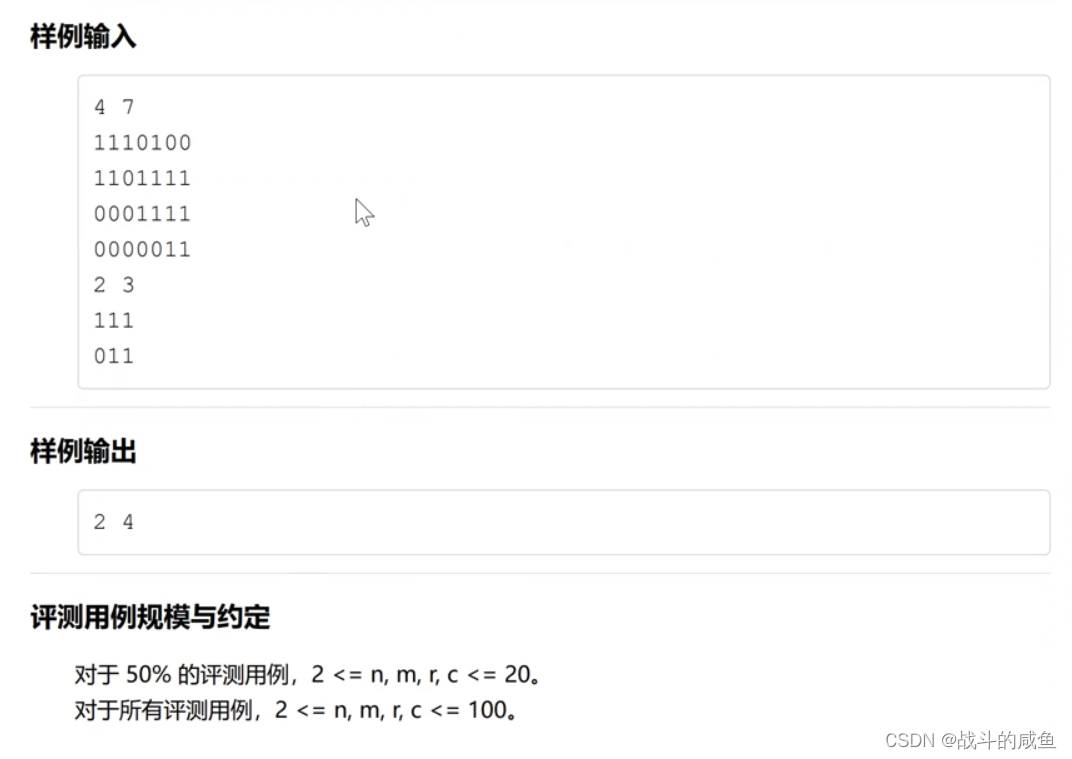
给出2个01矩阵，分别代表插板和插头的形状。插头伸出的部分（1）必须插在插孔（1）里，并且插头不能超过插板的边界。求出最小的a和b。

思路：

当时我看到这个题，脑子里一点思路也没有。菜菜菜。

官方说，这个题其实可以枚举。在整个插板

n·m

的范围里枚举a和b，对于每一种情况，再去遍历插头的01矩阵看看是否符合要求。粗略估计一下，时间复杂度大概是

n·m·r·c

，带入数据范围，结果大概是10^ 8。

10^ 8的数据范围在1s内可以跑完，不会超时。

（这个预判断超时的经验我也是第一次见，涨见识！！！）

代码：


输入输出风格为C。

#include<cstdio>
using namespace std;
int n, m, r, c;
char A[110][110], B[110][110];
bool ok(int a,int b) {
	for(int i=0; i<r; i++) {
		for(int j=0; j<c; j++) {
			if(B[i][j]=='1' && A[i+a][j+b]=='0') return false;
		}
	}
	return true;
}
int main()
{
	scanf("%d%d",&n, &m);
	for(int i=0; i<n; i++) {
		getchar();
		for(int j=0; j<m; j++) {
			scanf("%c",&A[i][j]);
		}
	}
	scanf("%d%d",&r,&c);
	for(int i=0; i<r; i++) {
		getchar();
		for(int j=0; j<c; j++) {
			scanf("%c",&B[i][j]);
		}
	}
	bool flag = false;
	int a,b;
	// 下标注意不要超出边界 
	for(int i=0; i<=n-r; i++) {
		for(int j=0; j<=m-c; j++) {
			if(ok(i,j)) {
				flag = true;
				a=i,b=j;
				break;
			}
		}
		if(flag == true) break;
	}
	if(flag==false) printf("NO");
	else printf("%d %d",a+1,b+1);
	return 0;
}

输入输出风格为C++，用string数组来存01矩阵好像会更简洁。

#include<iostream>
#include<string>
using namespace std;
string A[110], B[110];
int n, m, r, c;
bool ok(int a, int b) {
	for(int i=0; i<r; i++) {
		for(int j=0; j<c; j++) {
			if(B[i][j]=='1'&&A[i+a][j+b]=='0') return false;
		}
	}
	return true;
}
int main()
{
	cin>>n>>m;
	for(int i=0; i<n; i++) cin>>A[i];
	cin>>r>>c;
	for(int i=0; i<r; i++) cin>>B[i];
	for(int a=0; a<=n-r; a++) {
		for(int b=0; b<=m-c; b++ ) {
			if(ok(a,b)) {
				cout<<a+1<<" "<<b+1;
				return 0;
			}
		}
	}
	cout<<"NO";
	return 0;
}

注意：

• 存01矩阵的下标从0开始，而题目要求的输出格式中，下标从1开始，因此，输出a和b时记得都要+1。

公约数

题意：

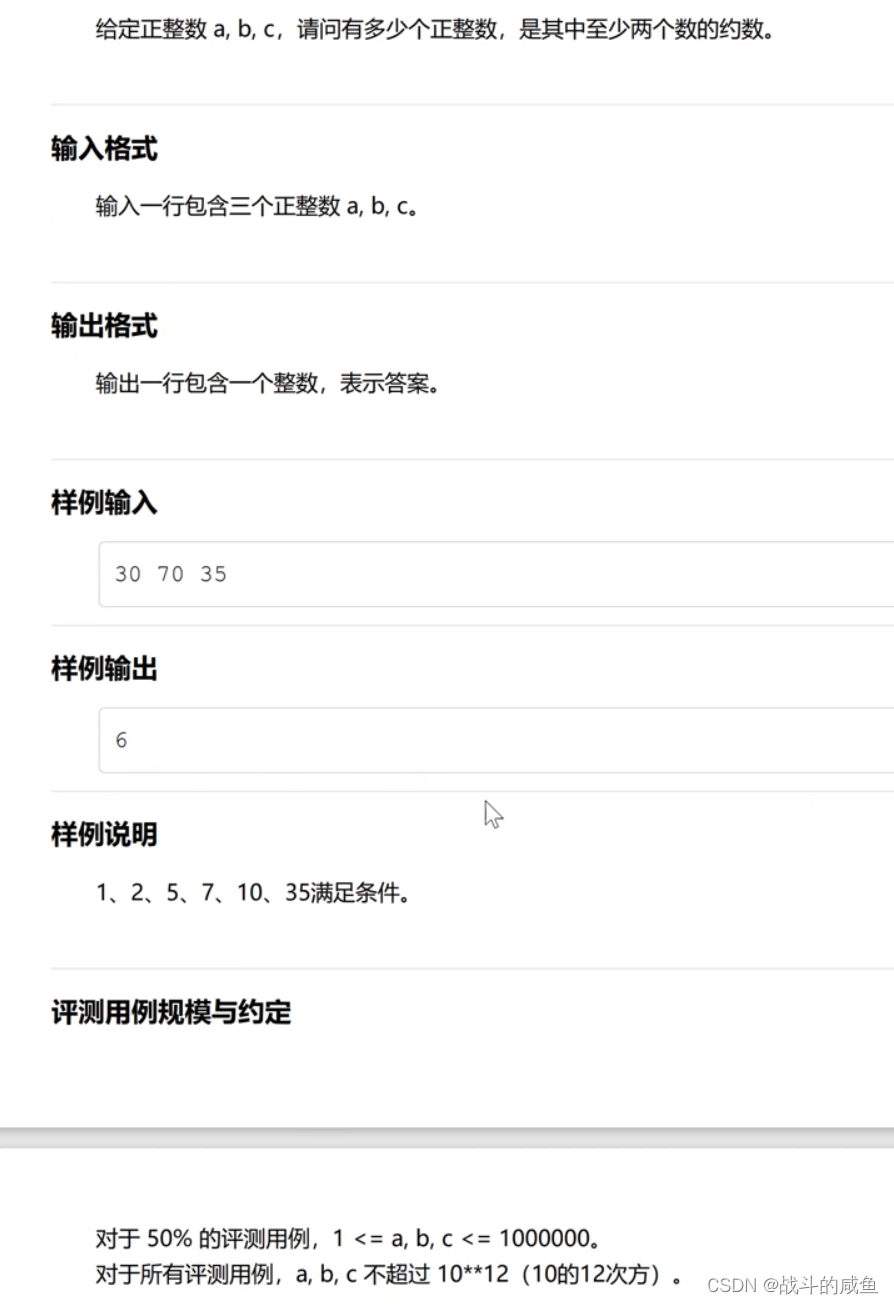
思路：

这道题我写的时候也是完全懵逼的，因为这个题要求3个正整数的约数的个数，显然会有很多重复的约数。而我的知识储备其实只有辗转相除法求2个数的最大公约数。脑子转不过弯，所以直接gg了。

官方题解思路如下：

首先这题数据范围到了10^12，显然不能纯暴力枚举，一定会超时，并且

存变量都要用long long

。

对a、b、c中的每2个数求一次所有的公约数，把这三次求得的约数都丢进set中，因为set本身的特性就是可以自动去重的，最后再用size()函数获得set里元素的个数。（因为我从来没有用过set这东西，自己看题完全反应不过来。后来了解了一下，

set就是专门处理去重

这个问题的）

现在问题变成了如何求2个数的所有公约数：先用辗转相除法求出2个数的最大公约数，然后

最大公约数的所有约数都是这2个数的公约数

。当然，求最大公约数的所有约数也不能纯暴力枚举，因为这个最大公约数很可能也有10^12量级，只需要枚举到根号下最大公约数即可，时间复杂度就降到了10 ^6。

代码：

#include<iostream>
#include<set>
#include<cmath>
using namespace std;
set<long long> st;
// 辗转相除法求gcd
long long Gcd(long long x, long long y) {
	if(x==0) return y;
	else return Gcd(y%x, x);
}
// 对任意x,y，求出它们所有的约数insert到set里
void judge(long long x, long long y) {
	long long gcd = Gcd(x,y);
	int sqr = sqrt(gcd);
	for(int i=1; i<=sqr; i++) {
		if(gcd%i==0) {
			st.insert(i);
			st.insert(gcd/i);
		}
	}
}

int main()
{
	long long a, b, c;
	cin>>a>>b>>c;
	judge(a,b);
	judge(a,c);
	judge(b,c);
	cout<<st.size();
	return 0;
}

汉诺塔

稍微瞄了一眼题解，感觉太复杂了，完全不是我可以cover的。不打算复现这个题了。

后记

8000+字数了哈哈。既然都看到这里了，麻烦给个赞啊~这对我来说是很大的鼓励！

—— 完 ——