Why

现有的专注于动态图的方法中，大多数都是都将边汇总为图快照，但这不能接近实时的检测，需要接收到边后立即识别出该边是否异常。在许多应用中的欺诈性或异常事件发生在微团簇或突然到达的可疑相似边缘组中，现有的方法都是检测单个边缘，且不能提供假阳率保证。本文提出的方法则是解决上述两个问题的。

1. Introduction

在专注于动态图的方法中，大多数方法都将边汇总为图快照。但是，为了最大程度地减少恶意活动的影响并尽快开始恢复，我们需要实时或接近实时地检测异常情况。接收到边后立即识别出该边是否异常。此外，由于在处理边缘流时顶点数量会增加，因此需要一种算法，该算法在图的尺寸中使用恒定内存。

在许多应用中的欺诈性或异常事件发生在微团簇或突然到达的可疑相似边缘组中，例如拒绝网络流量数据中的服务攻击和锁步行为。但是，以在线方式处理边缘流的现有方法（旨在检测单个令人惊讶的边缘（而不是微团簇），因此可能会丢失大量可疑活动。

在这项工作中，我们提出了MIDAS，它使用恒定的时间和内存来检测边缘流中的微团簇异常或突然到达的可疑相似边缘组。此外，通过使用原则上的假设检验框架，MIDAS为错误肯定概率提供了理论上的界限，而这些方法并未提供这些界限。然后，我们提出了包含时空关系的MIDAS-R。此外，我们还提出了MIDAS-F，它使用阈值来过滤异常边缘，以免它们对内部状态造成负面影响。

我们的主要贡献如下：

1）

流式微团簇检测：我们提出了一种新颖的流式方法来检测微团簇异常，需要持续的时间和内存。

2）

理论上的保证：在定理1中，我们为MIDAS的误报概率（假阳率）提供了保证。

3）有效性：我们的实验结果表明，MIDAS的准确性比基线方法高41％-55％（以AUC计），并且处理数据的速度比基线方法快130-929倍。

4）过滤异常：我们提出了一种变体MIDAS- F引入了两个修改，旨在滤除异常边缘，以防止它们对算法的内部数据结构产生负面影响。

2. Related Work

egonet

: 点：一个中心节点(ego)和他的邻居节点(alters)，边：ego和alters之间所有的边，组成的网络图。

主要分为三大类，在静态图上发现异常，在图流(快照)上发现异常，在边流上发现异常。仅最后一类中的2种方法适用于我们的任务，因为它们在边缘流上操作并输出计分器边缘。但是，如表1所示，两种方法都无法检测出微团簇，也无法提供对假阳性概率的保证。

在这里插入图片描述

3. Problem

算法的期望属性如下：

微团簇检测

：它应该检测突然出现的突然爆发的活动，这些突发具有许多重复的节点或边缘，我们称之为微团簇。
假阳率保证

：鉴于用户给定的概率水平
$\epsilon ϵ (比如1%)，算法应该是可调整的，以便提供最多为的假阳性概率 ϵ \epsilon ϵ (比如根据 ϵ \epsilon ϵ 调整threshold)。此外，虽然对误报概率的保证依赖于对数据分布的假设，但我们的目标是使我们的假设尽可能地弱。$
常数内存和更新时间

：为了在流设置中实现可伸缩性，该算法应在每个新到达的边缘上运行不变的内存和不变的更新时间。因此，其内存使用量和更新时间不应随流的长度或图中的节点数而增加。

4. MIDAS and MIDAS-R Algorithms

4.1 Overview

流假设测试方法

：我们描述了我们的MIDAS算法，该算法在基于假设测试的框架内使用流数据结构，使我们能够获得关于假阳性概率的保证。
检测和保证

：我们描述了用于确定某个点是否异常的决策程序，以及对误报概率的保证。
合并关系

：我们将方法扩展到MIDAS-R算法，该算法在时间和空间上合并了边之间的关系。

4.2 MIDAS: Streaming Hypothesis Testing Approach

4.2.1 Streaming Data Structures

在离线环境中，有许多时间序列方法可以检测到这种活动爆发。但是在联机设置中，因为限制内存使用量，即使是单个这样的时间序列，我们也无法跟踪。而且，有许多这样的源-目的地对，并且源和目的地的集合不是先验地固定的。

使用了两种Count-min sketch (

CMS

) 数据结构。

s_{uv}

$s_{u v}$

是

到当前时间

从u到v

总共

的条数。使用CMS数据结构来近似的保持这些

s_{uv}

$s_{u v}$

在一常量内存中，在任何时候，我们都可以查询数据结构以获得近似计数

\hat{s}_{uv}

$\overset{s}{^}_{u v}$

。让

a_{uv}

$a_{u v}$

是在

当前时间

刻度从u到v的边条数（不包含过去的时间刻度）。同样使用一个类似的CMS数据结构维护，与刚才不同的是这个进入下一个时间刻度将会被重置。因此这个CMS数据结构提供当前时刻t从u到v的近似值

\hat{a}_{uv}

$\overset{a}{^}_{u v}$

。

4.2.2 Hypothesis Testing Framework

对于给定的

\hat{s_{uv}}

$\overset{s_{u v}}{^}$

和

\hat{a_{uv}}

$\overset{a_{u v}}{^}$

，如何在一个有理有据的框架内检测微团簇？

一种方法是假设时间序列遵循特定的生成模型（比如，高斯分布），但是，这需要严格的高斯假设，如果数据遵循的分布非常不同，则可能导致过多的假阳性或阴性。取而代之的是，我们使用一个较弱的假设：当前时间（例如t =10）的平均水平（即边缘出现的平均速率）与当前时间（t <10）之前的平均水平相同。请注意，这避免了假设每个时间周期的任何特定分布，也避免了严格假设随时间推移的平稳性。

因此，我们可以将过去的边缘分为两类：当前时间（t = 10）和所有过去时间（t <10）。（t=10）的事件数是

\hat{a}_{uv}

$\overset{a}{^}_{u v}$

,过去时间（t<10）的事件数是

−

\hat{s}_{uv}-\hat{a}_{uv}

$\overset{s}{^}_{u v} - \overset{a}{^}_{u v}$

。

在

卡方拟合优化检验

下，卡方统计量定义为

−

)

(observed-expected)^2/expected

$(o b s e r v e d - e x p e c t e d)^{2} / e x p e c t e d$

类别上的总和。在这个例子上我们的类别是t=10和t<10,在平均水平假设检验下，总共的边是

s_{uv}

$s_{u v}$

(当前这个u到v)，在时间t=10期望的边数是

s_{uv}/t

$s_{u v} / t$

，t<10期望的边数就是剩下的

−

)

∗

(t-1)*s_{uv}/t

$(t - 1) * s_{u v} / t$

因此这个卡方检验量是：

在这里插入图片描述

这导致我们接下来的异常得分，利用该得分我们可以评估新到达的边（起点u终点v）。

在这里插入图片描述

4.3 Detection and Guarantees

虽然算法1计算了每条边的异常分数，但是并没有提供一个二元判断其是否异常。我们需要一个判断程序并保证假阳率最多是

\epsilon

$ϵ$

。直观地，关键思想是将CMS数据结构的近似保证与卡方随机变量的属性结合起来。

我们使用的CMS数据结构的主要特性是给予任何的

\epsilon

$ϵ$

和

v

$v$

，恰当的选择CMS数据结构的尺寸，概率至少为

−

1-\epsilon/2

$1 - ϵ / 2$

，估计值

\hat{a}_{uv}

$\overset{a}{^}_{u v}$

满足：

≤

(

)

\hat{a}_{uv}\le a_{uv} + vN_t\qquad(2)

$\overset{a}{^}_{u v} \leq a_{u v} + v N_{t} (2)$

这里

N_t

$N_{t}$

是在时间t时所有边的数量。由于CMS只能保证预测值大于真实值，另外有：

≤

(

)

s_{uv}\le \hat{s}_{uv}\qquad(3)

$s_{u v} \leq \overset{s}{^}_{u v} (3)$

定义先前分数的调整版本：

−

(

)

\tilde{a}_{uv} = \hat{a}_{uv}-vN_t\qquad(4)

$\tilde{a}_{u v} = \overset{a}{^}_{u v} - v N_{t} (4)$

为了获得其概率保证，我们的决策过程计

\tilde{a}_{uv}

$\tilde{a}_{u v}$

，并使用它来计算我们较早的统计信息的调整后的版本：

(

−

)

(

−

)

(

)

\tilde{X^2} = (\tilde{a}_{uv} – \dfrac{\hat{s}_{uv}}{t})^2 \dfrac{t^2}{\hat{s}_{uv}(t-1)} \qquad (5)

$\tilde{X^{2}} = (\tilde{a}_{u v} - \frac{s ^ _{u v}}{t})^{2} \frac{t ^{2}}{s ^ _{u v} ( t - 1 )} (5)$

Theorem 1

(假阳率边界)。使得

−

(

)

\chi_{1-\epsilon/2}^2(1)

$χ_{1 - ϵ / 2}^{2} (1)$

是具有1个自由度的卡方随机变量的分位数

−

1-\epsilon/2

$1 - ϵ / 2$

。然后：

(

−

(

)

(

)

P(\tilde{X^2}>\chi_{1-\epsilon/2}^2(1))<\epsilon \qquad (6)

$P (\tilde{X^{2}} > χ_{1 - ϵ / 2}^{2} (1)) < ϵ (6)$

换句话说，使用

\tilde{X^2}

$\tilde{X^{2}}$

作为我们的测试统计量和阈值为

−

(

)

\chi_{1-\epsilon/2}^2(1)

$χ_{1 - ϵ / 2}^{2} (1)$

使得假阳率最多为

\epsilon

$ϵ$

。

证明：

(

−

)

(

−

)

(

)

X^2 = (a_{uv}-\dfrac{s_{uv}}{t})^2 \dfrac{t^2}{s_{uv}(t-1)} \qquad (7)

$X^{2} = (a_{u v} - \frac{s _{u v}}{t})^{2} \frac{t ^{2}}{s _{u v} ( t - 1 )} (7)$

被定义以使其有卡方分布。因此：

(

≤

−

(

)

−

(

)

P(X^2 \le \chi_{1-\epsilon/2}^2(1))=1-\epsilon/2 \qquad (8)

$P (X^{2} \leq χ_{1 - ϵ / 2}^{2} (1)) = 1 - ϵ / 2 (8)$

同时，因为CMS保证我们有

(

≤

)

≥

−

(

)

P(\hat{a}_{uv} \le a_{uv}+vN_t) \ge 1-\epsilon/2 \qquad (9)

$P (\overset{a}{^}_{u v} \leq a_{u v} + v N_{t}) \geq 1 - ϵ / 2 (9)$

通过联合界限，事件（8）和（9）都至少以概率

−

1-\epsilon

$1 - ϵ$

,成立，在这种情况下:

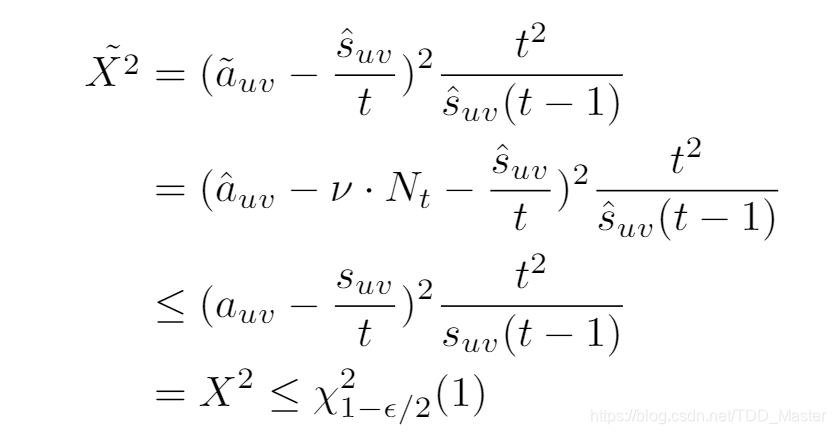
在这里插入图片描述

最后我们得出：

(

−

(

)

(

)

P(\tilde{X^2}>\chi_{1-\epsilon/2}^2(1))<\epsilon \qquad (10)

$P (\tilde{X^{2}} > χ_{1 - ϵ / 2}^{2} (1)) < ϵ (10)$

4.4 Incorporating Relations

在本节中，我们将描述MIDAS-R方法，该方法考虑了区域关系中的边缘：也就是说，其目的是将时间上或空间上相邻的边缘组合在一起。

时间关系

：不是像MIDAS只统计当前时刻的边数，我们允许一些时间上的灵活性，比如最近的边也应计入当前时间节拍，但应根据减少的重量进行修改。使用我们的CMS数据结构执行此操作的简单有效方式如下：在每次刻度线结束时，我们不会将CMS数据结构重置为固定值

a_{uv}

$a_{u v}$

，而是将其所有计数按固定比例缩放

∈

(

)

a \in (0,1)

$a \in (0, 1)$

。

空间关系

：想捕获一大组空间上邻近的边缘。比如，单个源IP地址突然为许多目的地创建了大量的边缘，或者一小组节点突然在它们之间创建了异常大量的边缘。我们使用的一个简单直觉是，在这两种情况中的任何一种情况下，我们都期望观察到突然出现大量边的节点。因此，我们可以像以前一样使用CMS数据结构来跟踪边缘计数，除了对与任何点u相邻的所有边缘进行计数之外。具体来说，我们创建CMS计数器

\hat{a}_u

$\overset{a}{^}_{u}$

和

\hat{s}_u

$\overset{s}{^}_{u}$

来近似计算与点u相邻的当前和总边计数。给定每个传入的edge（u，v），我们可以计算出三个异常分数：一个是边（u，v），如先前的算法；一个用于源节点u，一个用于目标节点v。最后，我们将三个分数取最大值进行组合。将三个分数相加的另一种可能性是取它们的总和。算法2总结了所得的MIDAS-R算法。

在这里插入图片描述

5. MIDAS-F: Filtering Anomalies

在MIDAS和MIDAS-R中，除了被分配了异常分数外，所有正常和异常边缘也始终记录在内部CMS数据结构中，无论其分数如何。但是这还包含一些异常边造成一种中毒影响可能会使得未来的异常漏洞而未被发现。让我们考虑一个拒绝服务攻击的简化情况，其中大量边缘在短时间内到达两个节点之间。 MIDAS和MIDAS-R分析可以分为三个阶段。

第一阶段，仅处理少数边缘时，异常分数很小。这个阶段不会持续太久，因为异常分数会随着出现异常边缘的次数而迅速增加。
第二阶段，一旦这两个计数器之间的差异变得明显，该算法将为那些可疑边缘返回较高的异常分数。
第三阶段，随着攻击的继续，即异常边缘继续到来，异常边缘边缘的预期计数将增加。结果，异常得分将逐渐降低，这可能导致假阴性，即异常边缘被视为正常边缘，这是由于CMS数据结构中包含异常而产生的“中毒”效应。

因此，为防止这些误报，我们引入了改进的滤波MIDAS（MIDAS-F）算法。以下提供了一个概述：

完善计分功能

：异常得分的新公式仅考虑当前时间滴答的信息，并使用先前时间滴答的平均值作为期望值。
有条件的合并

：源，目标和边缘的当前计数不再立即合并到总数中。我们在这个时间结束的时候决定是否合并以异常分数为条件。

5.1 Refined Scoring Function

在某个时间间隔内，尽管新的边不断出现，但我们只会为它们分配一个分数，而不会在它们到达后立即直接将其合并到我们的CMS数据结构中。这防止了异常边缘影响随后的异常得分，这可能导致假阴性。为了解决这个问题，我们改进了评分功能，以使用第5.2节中讨论的条件合并将边推迟合并到当前时间刻度的末尾。

如前所述，让

a_{uv}

$a_{u v}$

作为当前时间滴答声的边数（但不包括过去的时间滴答声）。但是与MIDAS和MIDAS-R不同的是，在MIDAS-F中，我们将

s_{uv}

$s_{u v}$

定义为从u到v到上一个时钟周期的边总数，不包括当前边计数。通过不立即包括当前边缘计数，我们防止了高

a_{uv}

$a_{u v}$

合并到

s_{uv}

$s_{u v}$

中，从而不会降低异常边缘的异常分数。

在MIDAS-F算法中，我们仍然遵循相同的假设：当前时间间隔的平均水平与当前时间间隔之前的平均水平相同，但是不将边沿分为过去和当前时间间隔两类，我们仅考虑当前时间间隔。与[22]的卡方统计相似，我们的统计如下：

在这里插入图片描述

a_{uv}

$a_{u v}$

和

s_{uv}

$s_{u v}$

可以使用CMS估计，获得近似值

\hat{a}_{uv}

$\overset{a}{^}_{u v}$

和

\hat{s}_{uv}

$\overset{s}{^}_{u v}$

。我们将使用这个新分数作为我们MIDAS-F算法的异常分数

(

)

−

(

−

)

(

)

score(u,v,t)=\dfrac{\hat{a}_{uv}+\hat{s}_{uv}-\hat{a}_{uv}t}{\hat{s}_{uv}(t-1)} \qquad (10)

$s c o r e (u, v, t) = \frac{a ^ _{u v} + s ^ _{u v} - a ^ _{u v} t}{s ^ _{u v} ( t - 1 )} (10)$

5.2 Conditional Merge

在时间间隔的最后，我们决定是否将

a_{uv}

$a_{u v}$

加入到

s_{uv}

$s_{u v}$

不取决于边(u,v)正常或者异常。

我们引入

c_{uv}

$c_{u v}$

来跟踪异常分数。每当时间间隔变化时，如果

c_{uv}

$c_{u v}$

小于预定阈值

\epsilon

$ϵ$

，那么对应的

a_{uv}

$a_{u v}$

将被加入到

s_{uv}

$s_{u v}$

；反之，期望得分，例如

(

−

)

s_{uv}/(t-1)

$s_{u v} / (t - 1)$

将被加入到

s_{uv}

$s_{u v}$

来保证。

平均水平不改变。我们只当缓存的分数

c_{uv}

$c_{u v}$

小于预定阈值

\epsilon

$ϵ$

时加入

a_{uv}

$a_{u v}$

，否则，这将减少将来时间间隔中异常边缘的异常分数。

在这里插入图片描述

我们也像MIDAS-R一样纳入时空关系。

Alg.4 总结了所得的MIDAS-F算法。它可以被分出如下两个部分，1）13到24行，我们在其中计算每个传入边的异常分数并更新相关计数。2）缩放和合并操作在6到12行，在每个间隔结束时，我们将当前计数乘以

a

$a$

并将其合并为总计数。

在这里插入图片描述

原文链接：https://blog.csdn.net/TDD_Master/article/details/115357011

Why

1. Introduction

2. Related Work

3. Problem

4. MIDAS and MIDAS-R Algorithms

4.1 Overview

4.2 MIDAS: Streaming Hypothesis Testing Approach

4.2.1 Streaming Data Structures

4.2.2 Hypothesis Testing Framework

4.3 Detection and Guarantees

4.4 Incorporating Relations

5. MIDAS-F: Filtering Anomalies

5.1 Refined Scoring Function

5.2 Conditional Merge

你可能也喜欢