关于查找树的总结【BST、AVL、红黑树、B树、B+树】

前言

关于各种查找树，可以说是面试、学习绕不开的点，正好最近我也有这种需求，就来进行一波总结与讨论
当然，这篇文章就类似于一篇使用指南、手册，如果要对哪一块进行一个深入的探究，那么还是需要再单独去查阅相关的文献与资料，如果和您的预期不符，请及时止损（因为本人很多时候都会抱着极大的期待去点开一篇文章，然而内容和标题都不符合
在这多叨叨一句，我认为知其然还需要知其所以然，探索一个啥知识点，就好就是用来干嘛的，从哪来的，有啥优点又有啥缺点，有缺点怎么解决，其实这些树之间，都是差不多有一个递进的关系的

一、BST（二叉搜索树）

BST的思路来源于二分查找，仔细想一想是不是还挺像的。
BST可以是一棵空树，也可以是一颗左子树不空，则左子树上所有结点的值均小于它的根结点的值；右子树不空，则右子树上所有结点的值均大于它的根结点的值的树。并且它的左右子树，也是BST。
比如{1，2，3，4，5，6，7，8}这么去构建一棵树，2为根节点，1为根节点的左子树，3为根节点的右子树，以此类推
总结一句话：BST

二叉搜索树的左子树的节点都小于根节点，右子树的节点都大于根节点

。
BST既有链表的快速插入与删除操作的特点，又有数组快速查找的优势。并且查找效率应该是O(log2n)
因此，BST快就快在这了，在查找数据的过程中，目标节点target和根结点root进行一个比较，如果target>root，那么应该往根节点的右子树去找；如果target<root，那么应该往根节点的左子树去找。
所以对于BST来说，如果对其进行种序遍历，也就是左根右的形式，得到的应该是一个递增的有序序列
判断是否为BST的代码如下：

class Solution:
    def isValidBST(self , root: TreeNode) -> bool:
        # write code here
        return self.search(root, float('-inf'), float('inf'))
    def search(self, root, left, right):
        if not root:
            return True
        if root.val < left or root.val > right:
            return False
        return self.search(root.left, left, root.val) and self.search(root.right, root.val, right)

二、AVL（平衡二叉树）

首先，为什么要有平衡二叉树，考虑这样一个情况，我们的BST只有左子树或者只有右子树的时候，那样的话我们再使用BST进行查找和对链表进行查找就没有区别了，查找的时间复杂度也从O(log2n)退化成了O(n)
观察其主要原因就是树形结构退化成了线形结构，所以想要保持查找效率就应该保持结构还是树形，因此引入AVL（平衡二叉树）
对于AVL来说，它可以是一棵空树，如果不是空树的话要求树的左右子节点的高度差不超过1，也就是说限制我们的数据组织的形式为一棵树
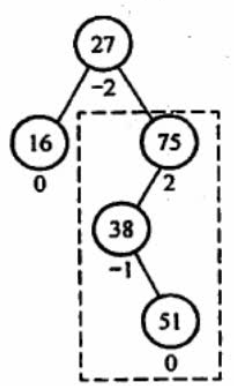
那如果说形状不满足二叉平衡树了怎们办呢？调整，在调整之前需要掌握一个概念：最小失衡树（第一个平衡因子的绝对值超过 1 的结点为根的子树称为最小不平衡子树）
想一想如果每一次我们的AVL失去平衡了都对他进行一个整体的调整，那该多麻烦啊！因此，我们每一次调整，应该仅仅调整失去平衡的最小的那棵树，假如是右子树的某棵子树失去平衡，那就调整那棵小一点的树。
接下来就涉及到调整了，调整分别有RR，RL，LL，LR
RR：右子树的右边插入节点导致失衡，这个时候把右子树的根节点提上来当父节点
LL：和RR反着来，左子树的左边插入节点导致失衡，就把左子树的根节点提上来当父节点
LR：这个比较复杂，在左子树的右边插入节点导致失衡，那么这个就需要左子树的右孩子提上来，然后进行一系列的合并
RL：在右子树的左边插入节点导致失衡，那么右子树的左孩子提上来，右子树当右子树，根节点做根节点
关于这几个旋转、调整的操作，主要还是靠悟
判断是否是AVL：简而言之就是看看左右子树的层数有没有问题，对于AVL来说每一棵子树都应该是AVL

class Solution:
    def IsBalanced_Solution(self , pRoot: TreeNode) -> bool:
        # write code here
        if not pRoot:
            return True
        left = self.depth(pRoot.left)
        right = self.depth(pRoot.right)
        if abs(left-right) > 1:
            return False
        return self.IsBalanced_Solution(pRoot.left) and self.IsBalanced_Solution(pRoot.right)
    def depth(self, root):
        if not root:
            return 0
        left = self.depth(root.left)
        right = self.depth(root.right)
        return max(left, right) + 1

三、红黑树

为什么要有红黑树？ – 有了AVL还引入红黑树的原因就在于：AVL的要求太严格了，只要稍有不慎就需要调整，换来换去的非常麻烦，因此红黑树通过牺牲严格的平衡，换取插入/删除时少量的旋转操作，整体性能优于AVL。
红黑树的插入删除在不平衡的时候，通过极少次的旋转就能完成
红黑树来自于2-3-4树，2-3-4树是阶数为4的B树。
一棵红黑树，大概就长这样
最重要的还是红黑树的那五个规则：

1.节点非黑即红。 2.根节点一定是黑色的。 3.不会出现连续的两个红节点。 4.任意路径上的黑色节点数目相等。 5.叶子结点一定是黑色的
用途：偏底层，毕竟大家做算法题的时候，也没见到让手写一棵红黑树的代码。比如Java中的TreeMap、Linux中的CFS调度算法等。
至于旋转这些就不在这过多赘述了，写本文就是为了水面试，要是被我碰上了也认了。怎么可能 – 染色或旋转。还有插入、删除，这些又够另起一片文章了。

四、B树、B+树

虽然平衡二叉树既有链表的快速插入与删除操作的特点，又有数组快速查找的优势，但是如果是针对磁盘的操作，每次旋转都要进行磁盘I/O，那么开销会特别的大，因此引入B树/B+树。只不过B+树比B树更好用而已。
B树：

每个节点都存着key以及value

，并且叶子节点指针为null
B+树：

只有叶子节点存储value

，叶子节点包含了这棵树的所有键值，并且每个叶子节点都有一个指向相邻叶子节点的指针
B树：

根结点至少有两个子结点;m个关键字就有m+1棵子树；所有的叶子结点都位于同一层;每个结点中关键字从小到大排列

，并且当该结点的孩子是非叶子结点时，该k-1个元素正好是k个子结点包含的元素的值域的分划
B+树：

叶子结点增加了指针进行连接

，即叶子结点间形成了链表；

非叶子结点只存关键字key

，不再存储数据；

m个关键字m棵子树

；
B树和B+树的区别：1.B树非叶子结点和叶子结点都存储数据，所以查询数据不稳定，有可能一下子就查到了，也有可能要找遍整棵树所以

时间复杂度最好为O(1),最坏为O(log n)

。；B+树只在叶子结点存储数据，非叶子结点存储关键字所以

时间复杂度固定为O(log n)

。 2.B+树叶子结点之间用链表相互连接，因而只需扫描叶子结点的链表就可以完成一次遍历操作，B树只能通过中序遍历
B+树比B树更适合更适合做数据库索引和文件索引
理由：1. B+树的查询效率稳定。 2.B+树更加适应磁盘的特性，相比B树减少了I/O读写的次数（B+树的非叶子结点只存关键字不存数据，因此B+树的树形比较矮胖）3.B+树叶子结点用链表链接，所以查找数据只需要进行一次扫描。

原文链接：https://blog.csdn.net/qq_44197482/article/details/123574771

前言

一、BST（二叉搜索树）

二、AVL（平衡二叉树）

三、红黑树

四、B树、B+树

你可能也喜欢