在做线性回归预测时候,为了提高模型的泛化能力,经常采用多次线性函数建立模型
f = k*x + b 一次函数
f = a*x^2 + b*x + w 二次函数
f = a*x^3 + b*x^2 + c*x + w 三次函数等等
泛化:
对未训练过的数据样本进行预测。
欠拟合:
由于对训练样本的拟合程度不够,导致模型的泛化能力不足。
过拟合:
训练样本拟合非常好,并且学习到了不希望学习到的特征,导致模型的泛化能力不足。
在建立超过一次函数的线性回归模型之前,要对默认特征生成多项式特征再输入给模型 1 from sklearn.linear_model import LinearRegression
2 import numpy as np
3 import matplotlib.pyplot as plt
4
5 '''
6 在做线性回归预测时候,
7 为了提高模型的泛化能力,经常采用多次线性函数建立模型
8
9 f = k*x + b 一次函数
10 f = a*x^2 + b*x + w 二次函数
11 f = a*x^3 + b*x^2 + c*x + w 三次函数
12
13
14 泛化:
15 对未训练过的数据样本进行预测。
16
17 欠拟合:
18 由于对训练样本的拟合程度不够,导致模型的泛化能力不足。
19
20 过拟合:
21 训练样本拟合非常好,并且学习到了不希望学习到的特征,导致模型的泛化能力不足。
22
23
24 在建立超过一次函数的线性回归模型之前,要对默认特征生成多项式特征再输入给模型
25
26 下面模拟 根据蛋糕的直径大小 预测蛋糕价格
27 '''
28
29
30 # 样本的训练数据,特征和目标值
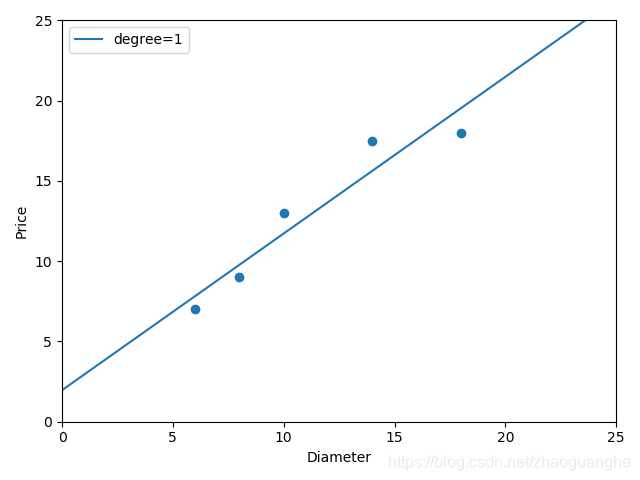
31 x_train = [[6], [8], [10], [14], [18]]
32 y_train = [[7], [9], [13], [17.5], [18]]
33
34 # 一次线性回归的学习与预测
35 # 线性回归模型 学习
36 regressor = LinearRegression()
37 regressor.fit(x_train, y_train)
38 # 画出一次线性回归的拟合曲线
39 xx = np.linspace(0, 25, 100) # 0到16均匀采集100个点做x轴
40 xx = xx.reshape(xx.shape[0], 1)
41 yy = regressor.predict(xx) # 计算每个点对应的y
42 plt.scatter(x_train, y_train) # 画出训练数据的点
43 plt1, = plt.plot(xx, yy, label="degree=1")
44 plt.axis([0, 25, 0, 25])
45 plt.xlabel("Diameter")
46 plt.ylabel("Price")
47 plt.legend(handles=[plt1])
48 plt.show()一次线性函数拟合曲线的结果,是欠拟合的情况: