五一之后就开始实习了,接触的第一件事就是解析正则,于是开始学习正则转DFA的知识。看了很多帖子,始终在状态move中的解析一带而过,最终在网易云课堂的一门课中找到答案。http://study.163.com/course/courseMain.htm?courseId=1002830012。我从中摘抄部分内容如下,如果觉得有用请去云课堂里继续学习。非常感谢这位老师。
摘抄:
大家好,欢迎大家来到coding迪斯尼,上一节我们研究了如何使用NFA识别输入字符串,同时提出了来个概念,一个是ε闭包操作,一个是move得到转移集合。这两个操作在我们今天的主题,将NFA转换为DFA的算法中将占据主导地位。我们任然以上一节用到的NFA状态机为例子,看看它是怎么转换为DFA的
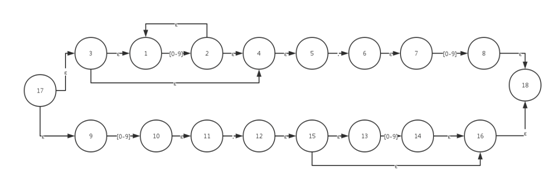
NFA转DFA算法:
我们先获取NFA的起始节点,然后计算它的ε闭包:
ε-closure({17}) = { 17, 3 , 1, 4, 5, 9}
我们知道,处于ε闭包中的任何一个状态节点时,我们可以不用输入任何字符就可以直达其他节点,因此,闭包中的所有节点其实可以等价于一个节点,这个节点就可以作为NFA对应的DFA中的一个节点。因此我们把集合{ 17, 3 , 1, 4, 5, 9}
对应于一个节点,记为S0:
(S0, { 17, 3 , 1, 4, 5, 9})
于此同时把上面的节点标记加入一个队列中,最为队列的开头:
[(S0, { 17, 3 , 1, 4, 5, 9})]
NFA状态机可接受的字符是数字字符和字符 ’.’ ,接下来我们计算S0对数字字符和字符’.’ 的转移集合:
Move(S0, .) = Move({ 17, 3 , 1, 4, 5, 9}, . ) = {6}
接着计算{6}的ε闭包:
ε-closure({6}) = {6,7}, 然后看看{6,7}在上面的队列中是否存在,由于当前队列只有一个元素:[(S0, { 17, 3 , 1, 4, 5, 9})], 所以{6,7}在队列中不存在,于是我们把{6,7}当做DFA的第二个状态节点记做(S1, {6,7}), 把它加入到队列中:
[(S0, { 17, 3 , 1, 4, 5, 9})]->[(S1, {6,7})]
这样我们就有了两个节点的对应关系 S0-(.)->S1.
我们再计算S0对应数字字符时所得的转移集合:
Move(S0, D) = Move({ 17, 3 , 1, 4, 5, 9}, D) = {2, 10}
然后对{2,10}做闭包操作:
ε-closure({2,10}) = {2,10,4,5,1,11}
看看队列中是否有{2,10,4,5,1,11}对应的节点,由于没有对应节点,所以该集合可作为DFA的一个节点,记做(S2, {2,10,4,5,1,11}). 然后把它加入队列:
[(S0, { 17, 3 , 1, 4, 5, 9})]->[(S1, {6,7})]->[(S2, {2,10,4,5,1,11})]
于是我们又有了一个节点对应关系:
S0-(D)->S2
最后我们得到DFA的三节点关系图:
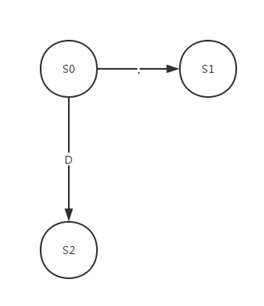
大家要注意,从图上看S0 到 S2 只有一条边,但是D代表的是数字字符的集合[0-9],所以实际上S0到S2有10条边,也就是S0有10条出去的边,边对应的字符分别是0,1,2…9, 这十条边都指向S2,上图为了简明,所以把这十条边抽象为1条边,在后续我们代码中,构造的DFA将会有10条边指向S2,这个差别大家要留心。
接下来我们计算S1对应数字字符和字符’.’所得到的转移集合:
Move(S1, .) = Move({6,7}, .) = NULL
由于转移集合是空,因此我们不做考虑,再看S1对应D的转移集合
Move(S1, D) = Move({6,7}, D) = {8}
ε-closure({8}) = {8,18}.
在队列中看看有没有{8.18}对应的节点,由于没有所以{8,18}可作为DFA新的节点,记为(S3, {8,18}),并加入队列:
[(S0, { 17, 3 , 1, 4, 5, 9})]->[(S1, {6,7})]->[(S2, {2,10,4,5,1,11})]->[(S3, {8,18})]
同时意味着节点S1与节点S3有对应关系: S1-(D)->S3, 特别需要注意的是,S3的NFA节点集合中包含了NFA的终结节点18,所以S3是一个具有接受状态的节点,于是我们得到DFA如下:
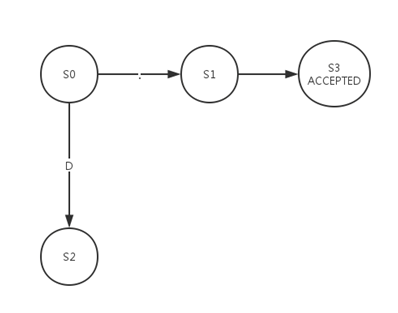
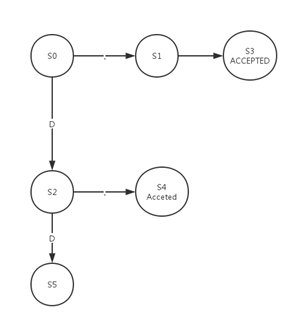
接下来我们计算S2的对应数字字符和字符’.’的转移集合:
Move(S2, .) = Move({2,10,4,5,1,11}, .) = {6,12}
ε-closure({6,12}) = {6,12,7,15,13,16,18}
查看队列看看有没有上面闭包集合对应的点,由于没有,所以上面闭包可以对应一个新的DFA节点,记为 (S4, {6,12,7,15,13,16,18})由于闭包集合含有NFA接受节点18, 所以S4是一个接受节点,把S4加入队列:
[(S0, { 17, 3 , 1, 4, 5, 9})]->[(S1, {6,7})]->[(S2, {2,10,4,5,1,11})]->[(S3, {8,18})]->
[(S4, {6,12,7,15,13,16,18})]
同时我们得到对应关系 S2-(.)->S4
我们计算S2对应D的转移集合:
Move(S2, D) = Move({2,10,4,5,1,11}, D) = {2}
ε-closure({2}) = {2, 1, 4, 5}
检测一下闭包集合是否在队列中,由于不在,所以它可以对应于DFA一个新节点记为 (S5, {2,1,4,5}), 把它加入队列:
[(S0, { 17, 3 , 1, 4, 5, 9})]->[(S1, {6,7})]->[(S2, {2,10,4,5,1,11})]->[(S3, {8,18})]->
[(S4, {6,12,7,15,13,16,18})]->[(S5, {2,1,4,5})]
我们又得到一个对应关系S2-(D)->S5,这样DFA状态图又更新为: