ITRS 与 GCRS 之间的坐标转换

1. ITRS 与 GCRS 之间的坐标转换

由于地球自转, 地球坐标系并不是一个惯性坐标系, 而轨道计算是建立在牛顿力学的基础上的, 因此定轨工作不能在地球坐标系中进行。如前所述, GCRS 是一个相当不错的准惯性坐标系, 定轨工作一般都在该坐标系中进行，但是用户利用卫星导航定位系统最终是为了求得在地球坐标系中的位置和速度, 因而还必须把 GCRS 中所求得的卫星轨道(卫星位置和速度) 转换到地球坐标系 ITRS(WGS 84) 中去。

ITRS 与 GCRS 之间有下列转换关系:

)

[

]

[

]

[

]

[

]

(

)

\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)_{\mathrm{GCRS}}=[\boldsymbol{P}][\boldsymbol{N}][\boldsymbol{R}][\boldsymbol{W}]\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)_{\mathrm{ITRS}}

$⎝ ⎛ X Y Z ⎠ ⎞_{GCRS} = [P] [N] [R] [W] ⎝ ⎛ X Y Z ⎠ ⎞_{ITRS}$

)

ITRS

[

]

−

[

]

−

[

]

−

[

]

−

(

)

\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)_{\text {ITRS }}=[\boldsymbol{W}]^{-1}[\boldsymbol{R}]^{-1}[\boldsymbol{N}]^{-1}[\boldsymbol{P}]^{-1}\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)_{\mathrm{GCRS}}

$⎝ ⎛ X Y Z ⎠ ⎞_{ITRS} = [W]^{- 1} [R]^{- 1} [N]^{- 1} [P]^{- 1} ⎝ ⎛ X Y Z ⎠ ⎞_{GCRS}$

式中,

]

[\boldsymbol{P}]

$[P]$

为岁差矩阵;

]

[\boldsymbol{N}]

$[N]$

为章动矩阵;

]

[\boldsymbol{R}]

$[R]$

为地球自转矩阵;

]

[\boldsymbol{W}]

$[W]$

为极移矩阵。考虑到 IGS 已完成了坐标转换工作, 在精密星历中直接给出了卫星质心在 ITRS 中的位置和速度, 而广播星历的精度有限, 允许采用一些近似的转换方法, 因此在下面的坐标转换中, 我们仍采用经典的转换方法与术语 (与 IS-GPS-200D 及 IS-GPS-705 中给出的方法基本一致)。高精度的严格方法可参阅 IAU 的决议文件和空间大地测量学等参考资料。

（1）把 GCRS 转换至观测时刻

t_i

$t_{i}$

的平天球坐标系

我们知道, GCRS 是参考时刻

2000.0

t_0=\mathrm{J} 2000.0

$t_{0} = J 2000.0$

时的平天球坐标系, 要把它转换为观测时刻

t_i

$t_{i}$

时的平天球坐标系, 只要考虑

−

]

\left[t_0-t_i\right]

$[t_{0} - t_{i}]$

时间段内的岁差改正, 即乘上

]

−

[\boldsymbol{P}]^{-1}

$[P]^{- 1}$

矩阵即可。

（2）把

t_i

$t_{i}$

时的平天球坐标系转换为同一时刻的真天球坐标系

要把观测时刻

t_i

$t_{i}$

时的平天球坐标系转换为真天球坐标系, 只需顾及该时刻的章动, 即只需乘上

]

−

[\boldsymbol{N}]^{-1}

$[N]^{- 1}$

矩阵即可。

（3）把

t_i

$t_{i}$

时的真天球坐标系转换为同一时刻的真地球坐标系

我们知道, 真天球坐标系

X

$X$

轴是指向该时刻的真春分点

\gamma

$γ$

的,而真地球坐标系的

X

$X$

轴是指向起始子午线与赤道的交点,两者之间的夹角称为格林尼治真恒星时 GAST 。其计算公式如下:

∘

(

50.54841

8640184.812866

⋅

0.093104

⋅

−

6.2

−

⋅

)

cos

⁡

(

)

\begin{aligned} \text { GAST }=& \frac{360^{\circ}}{24^{\mathrm{h}}}\left(\mathrm{UT} 1+6 \mathrm{~h} 41 \mathrm{~m} 50.54841 \mathrm{~s}+8640184.812866 \mathrm{~s} \cdot \mathrm{t}+0.093104 \mathrm{~s} \cdot t^2\right.\\ &\left.-6.2 \mathrm{~s} \times 10^{-6} \cdot t^3\right)+\Delta \Psi_{\cos }(\bar{\varepsilon}+\Delta \varepsilon) \end{aligned}

$GAST = \frac{36 0 ^{\circ}}{2 4 ^{h}} (UT 1 + 6 h 41 m 50.54841 s + 8640184.812866 s \cdot t + 0.093104 s \cdot t^{2} - 6.2 s \times 1 0^{- 6} \cdot t^{3}) + Δ Ψ_{c o s} (\overset{ε}{ˉ} + Δ ε)$

式中,

t

$t$

为离

2000.0

\mathrm{J} 2000.0

$J 2000.0$

的儒略世纪数;

\bar{\varepsilon}

$\overset{ε}{ˉ}$

为仅顾及岁差时的黄赤交角,

∘

′

21.44

′

−

\bar{\varepsilon}=23^{\circ} 26^{\prime} 21.448^{\prime \prime}-

$\overset{ε}{ˉ} = 2 3^{\circ} 2 6^{'} 21.44 8^{''} -$

′

⋅

−

0.0005

′

⋅

0.00181

′

⋅

;

46.815^{\prime \prime} \cdot t-0.00059^{\prime \prime} \cdot t^2+0.001813^{\prime \prime} \cdot t^3 ; \Delta \psi

$46.81 5^{''} \cdot t - 0.0005 9^{''} \cdot t^{2} + 0.00181 3^{''} \cdot t^{3}; Δ ψ$

′

⋅

−

0.0005

′

⋅

0.00181

′

⋅

;

46.815^{\prime \prime} \cdot t-0.00059^{\prime \prime} \cdot t^2+0.001813^{\prime \prime} \cdot t^3 ; \Delta \Psi

$46.81 5^{''} \cdot t - 0.0005 9^{''} \cdot t^{2} + 0.00181 3^{''} \cdot t^{3}; ΔΨ$

为黄经章动;

\Delta \varepsilon

$Δ ε$

为交角章动;

\mathrm{UT1}

$UT1$

则可据观测时的 UTC 和( UTC-UT1) 值求得。

把真天球坐标系绕

Z

$Z$

轴旋转 GAST 角后就能转换到真地球坐标系, 旋转矩阵

\boldsymbol{R}

$R$

为:

(

cos

⁡

sinGAST

⁡

−

sinGAST

⁡

cos

⁡

)

\boldsymbol{R}=\left(\begin{array}{ccc} \cos G A S T & \operatorname{sinGAST} & 0 \\ -\operatorname{sinGAST} & \cos G A S T & 0 \\ 0 & 0 & 1 \end{array}\right)

$R = ⎝ ⎛ cos G A ST - sinGAST 0 sinGAST cos G A ST 0 001 ⎠ ⎞$

（4）把

t_i

$t_{i}$

时的真地球坐标系转换为 ITRS (WGS 84)

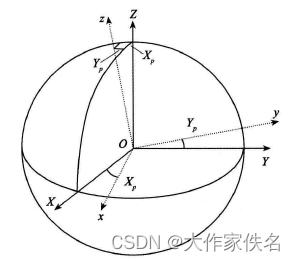
在这里插入图片描述

从上图可以看出, 只需要将

t_i

$t_{i}$

时的真地球坐标系绕

y

$y$

轴旋转

−

)

\left(-X_p\right)

$(- X_{p})$

角后,然后再绕

x

$x$

轴旋转

−

)

\left(-Y_p\right)

$(- Y_{p})$

角后, 就可以把直地球坐标系

−

O-x y z

$O - x yz$

转换为

⁡

(

)

\operatorname{ITRS}(\mathrm{WGS} 84)

$ITRS (WGS 84)$

坐标系

−

。

O-X Y Z_{\text {。 }}

$O - X Y Z_{。}$

即

)

(

−

)

(

−

)

(

)

(

cos

⁡

−

sin

⁡

sin

⁡

cos

⁡

)

(

cos

⁡

sin

⁡

−

sin

⁡

cos

⁡

)

(

)

\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)=\boldsymbol{R}_x\left(-Y_p\right) \boldsymbol{R}_y\left(-X_p\right)\left(\begin{array}{l} x \\ y \\ z \end{array}\right)=\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos Y_p & -\sin Y_p \\ 0 & \sin Y_p & \cos Y_p \end{array}\right)\left(\begin{array}{ccc} \cos X_p & 0 & \sin X_p \\ 0 & 1 & 0 \\ -\sin X_p & 0 & \cos X_p \end{array}\right)\left(\begin{array}{l} x \\ y \\ z \end{array}\right)

$⎝ ⎛ X Y Z ⎠ ⎞ = R_{x} (- Y_{p}) R_{y} (- X_{p}) ⎝ ⎛ x y z ⎠ ⎞ = ⎝ ⎛ 100 0 cos Y_{p} sin Y_{p} 0 - sin Y_{p} cos Y_{p} ⎠ ⎞ ⎝ ⎛ cos X_{p} 0 - sin X_{p} 010 sin X_{p} 0 cos X_{p} ⎠ ⎞ ⎝ ⎛ x y z ⎠ ⎞$

由于极移值

X_p

$X_{p}$

和

Y_p

$Y_{p}$

都是小于

′

0.5^{\prime \prime}

$0. 5^{''}$

的微小值, 所以

⁡

cos

⁡

sin

⁡

\cos X_p=\cos Y_p=1, \sin X_p=X_p

$cos X_{p} = cos Y_{p} = 1, sin X_{p} = X_{p}$

,

⁡

\sin Y_p=Y_p

$sin Y_{p} = Y_{p}$

, 于是有

:

$:$

)

(

−

)

(

−

)

(

)

(

−

)

(

)

[

]

(

)

\left(\begin{array}{l} X \\ Y \\ Z \end{array}\right)=\left(\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & -Y_p \\ 0 & Y_p & 1 \end{array}\right)\left(\begin{array}{ccc} 1 & 0 & X_p \\ 0 & 1 & 0 \\ -X_p & 0 & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \\ z \end{array}\right)=\left(\begin{array}{ccc} 1 & 0 & X_p \\ 0 & 1 & -Y_p \\ -X_p & Y_p & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \\ z \end{array}\right)=[\boldsymbol{W}]\left(\begin{array}{l} x \\ y \\ z \end{array}\right)

$⎝ ⎛ X Y Z ⎠ ⎞ = ⎝ ⎛ 100 01 Y_{p} 0 - Y_{p} 1 ⎠ ⎞ ⎝ ⎛ 10 - X_{p} 010 X_{p} 01 ⎠ ⎞ ⎝ ⎛ x y z ⎠ ⎞ = ⎝ ⎛ 10 - X_{p} 01 Y_{p} X_{p} - Y_{p} 1 ⎠ ⎞ ⎝ ⎛ x y z ⎠ ⎞ = [W] ⎝ ⎛ x y z ⎠ ⎞$

出自：《GPS测量与数据处理》第二章。

原文链接：https://blog.csdn.net/wokaowokaowokao12345/article/details/127382390

1. ITRS 与 GCRS 之间的坐标转换

你可能也喜欢