一.简介
这篇博文主要是讲解两种算法
一个是最小生成树算法(最小代价树)
里面包含了两种算法:
Prim算法和Kruskal算法(PK算法)用于把图中的点全部连接起来
另一个是单源最短路径算法:
Dijkstra算法和Floyd算法(简称DF二连算法)用于求解单源最短路径
二.算法简介
对于最小代价生成树的Prim、Kruskal算法,两种算法的主要核心思想是
贪心算法
。
Prim算法
是从任意一个顶点开始,每次选择一个与当前顶点集最近的一个顶点,并将两顶点之间的边加入到树中,其实就是说在当前顶点集所可以辐射到的边中选择最小的一条边(需要判断该边是否已经在最小生成树中),其实就是一个排序问题,然后贪心选取最小值。
Kruskal算法
则是另外一种思维,选择从边开始,把所有的边按照权值先从小到大排列,接着按照顺序选取每条边(贪心思想),如果这条边的两个端点不属于同一集合,那么就将它们合并,直到所有的点都属于同一个集合为止,其实就是基于
并查集的贪心算法
。两种算法各有不同,Prim算法的时间复杂度为
,n表示顶点数目,这跟它的初心还是蛮符合的,毕竟它是从顶点出发,可以从公式中看出Prim算法的时间复杂度与网络中的边无关,所以适合来求解边稠密的网的最小代价生成树。而Kruskal算法恰恰相反,它适合来求边稀疏的网的最小代价生成树,时间复杂度为
,e表示网络中的边数。
对于最短路径算法的Dijkstra、Floyd算法;
Dijkstra算法
是求从某个源点到其余各个顶点的最短路径(单源最短路径),时间复杂度为
,主要思想为每次在未确定的顶点中选取最短的路径,并把最短路径的顶点设为确定值,然后再由源点经该点出发来松弛其他顶点的路径的值,重复以上步骤最后得到就是最短路径了。而
Floyd算法
针对的问题是求每对顶点之间的最短路径,相当于把Dijkstra算法执行了n遍(实际上并不是这样做),所以Floyd算法的时间复杂度为
。但实际上Floyd算法核心代码就有五行,主要用公式
来不断优化带权邻接矩阵,最后得到矩阵就是每对顶点之间的最短距离了。
三.算法思路与代码
Prim算法与Kruskal算法(最小生成树)
prim算法基本思路
:所有节点分成两个group,一个为已经选取的selected_node(为list类型),一个为candidate_node,首先任取一个节点加入到selected_node,然后遍历头节点在selected_node,尾节点在candidate_node的边,选取符合这个条件的边里面权重最小的边,加入到最小生成树,选出的边的尾节点加入到selected_node,并从candidate_node删除。直到candidate_node中没有备选节点(这个循环条件要求所有节点都有边连接,即边数要大于等于节点数-1,循环开始前要加入这个条件判断,否则可能会有节点一直在candidate中,导致死循环)。
kruskal算法基本思路:
先对边按权重从小到大排序,先选取权重最小的一条边,如果该边的两个节点均为不同的分量,则加入到最小生成树,否则计算下一条边,直到遍历完所有的边。
普里姆算法
(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点(英语:Vertex (graph theory)),且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克(英语:Vojtěch Jarník)发现;并在1957年由美国计算机科学家罗伯特·普里姆(英语:Robert C. Prim)独立发现;1959年,艾兹格·迪科斯彻再次发现了该算法。因此,在某些场合,普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆-亚尔尼克算法。
算法简单描述
1).输入:一个加权连通图,其中顶点集合为V,边集合为E;
2).初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
3).重复下列操作,直到Vnew = V:
a.在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
b.将v加入集合Vnew中,将<u, v>边加入集合Enew中;
4).输出:使用集合Vnew和Enew来描述所得到的最小生成树。
Kruskal算法
是一种用来寻找最小生成树的算法,由Joseph Kruskal在1956年发表。用来解决同样问题的还有Prim算法和Boruvka算法等。三种算法都是贪婪算法的应用。和Boruvka算法不同的地方是,Kruskal算法在图中存在相同权值的边时也有效。
2.算法简单描述
1).记Graph中有v个顶点,e个边
2).新建图Graphnew,Graphnew中拥有原图中相同的e个顶点,但没有边
3).将原图Graph中所有e个边按权值从小到大排序
4).循环:从权值最小的边开始遍历每条边 直至图Graph中所有的节点都在同一个连通分量中
if 这条边连接的两个节点于图Graphnew中不在同一个连通分量中
添加这条边到图Graphnew中
#coding=utf-8
class Graph(object):
def __init__(self, maps):
self.maps = maps
self.nodenum = self.get_nodenum()
self.edgenum = self.get_edgenum()
def get_nodenum(self):
return len(self.maps)
def get_edgenum(self):
count = 0
for i in range(self.nodenum):
for j in range(i):
if self.maps[i][j] > 0 and self.maps[i][j] < 9999:
count += 1
return count
def kruskal(self):
res = []
if self.nodenum <= 0 or self.edgenum < self.nodenum-1:
return res
edge_list = []
for i in range(self.nodenum):
for j in range(i,self.nodenum):
if self.maps[i][j] < 9999:
edge_list.append([i, j, self.maps[i][j]])#按[begin, end, weight]形式加入
edge_list.sort(key=lambda a:a[2])#已经排好序的边集合
group = [[i] for i in range(self.nodenum)]
for edge in edge_list:
for i in range(len(group)):
if edge[0] in group[i]:
m = i
if edge[1] in group[i]:
n = i
if m != n:
res.append(edge)
group[m] = group[m] + group[n]
group[n] = []
return res
def prim(self):
res = []
if self.nodenum <= 0 or self.edgenum < self.nodenum-1:
return res
res = []
seleted_node = [0]
candidate_node = [i for i in range(1, self.nodenum)]
while len(candidate_node) > 0:
begin, end, minweight = 0, 0, 9999
for i in seleted_node:
for j in candidate_node:
if self.maps[i][j] < minweight:
minweight = self.maps[i][j]
begin = i
end = j
res.append([begin, end, minweight])
seleted_node.append(end)
candidate_node.remove(end)
return res
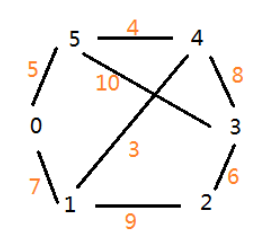
max_value = 9999
row0 = [0,7,max_value,max_value,max_value,5]
row1 = [7,0,9,max_value,3,max_value]
row2 = [max_value,9,0,6,max_value,max_value]
row3 = [max_value,max_value,6,0,8,10]
row4 = [max_value,3,max_value,8,0,4]
row5 = [5,max_value,max_value,10,4,0]
maps = [row0, row1, row2,row3, row4, row5]
graph = Graph(maps)
print('邻接矩阵为\n%s'%graph.maps)
print('节点数据为%d,边数为%d\n'%(graph.nodenum, graph.edgenum))
print('------最小生成树kruskal算法------')
print(graph.kruskal())
print('------最小生成树prim算法')
print(graph.prim())
Dijkstra算法和Floyd算法(单源最短路径)
Dijkstra算法讲解
基本思想
1.通过Dijkstra计算图G中的最短路径时,需要指定起点s(即从顶点s开始计算)。
2.此外,引进两个集合S和U。S的作用是记录已求出最短路径的顶点(以及相应的最短路径长度),而U则是记录还未求出最短路径的顶点(以及该顶点到起点s的距离)。
3.初始时,S中只有起点s;U中是除s之外的顶点,并且U中顶点的路径是”起点s到该顶点的路径”。然后,从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 然后,再从U中找出路径最短的顶点,并将其加入到S中;接着,更新U中的顶点和顶点对应的路径。 … 重复该操作,直到遍历完所有顶点。
操作步骤
1.初始时,S只包含起点s;U包含除s外的其他顶点,且U中顶点的距离为”起点s到该顶点的距离”[例如,U中顶点v的距离为(s,v)的长度,然后s和v不相邻,则v的距离为∞]。
2.从U中选出”距离最短的顶点k”,并将顶点k加入到S中;同时,从U中移除顶点k。
3.更新U中各个顶点到起点s的距离。之所以更新U中顶点的距离,是由于上一步中确定了k是求出最短路径的顶点,从而可以利用k来更新其它顶点的距离;例如,(s,v)的距离可能大于(s,k)+(k,v)的距离。
4.重复步骤(2)和(3),直到遍历完所有顶点。
使用二维矩阵来存储边的权重

inf = float('inf')
matrix_distance = [[0,1,12,inf,inf,inf],
[inf,0,9,3,inf,inf],
[inf,inf,0,inf,5,inf],
[inf,inf,4,0,13,15],
[inf,inf,inf,inf,0,4],
[inf,inf,inf,inf,inf,0]]
def dijkstra(matrix_distance, source_node):
inf = float('inf')
# init the source node distance to others
dis = matrix_distance[source_node]
node_nums = len(dis)
flag = [0 for i in range(node_nums)]
flag[source_node] = 1
for i in range(node_nums-1):
min = inf
#find the min node from the source node
for j in range(node_nums):
if flag[j] == 0 and dis[j] < min:
min = dis[j]
u = j
flag[u] = 1
#update the dis
for v in range(node_nums):
if flag[v] == 0 and matrix_distance[u][v] < inf:
if dis[v] > dis[u] + matrix_distance[u][v]:
dis[v] = dis[u] + matrix_distance[u][v]
return dis
print(dijkstra(matrix_distance, 1))
Floyd算法详解
算法思想
Floyd算法是一个经典的动态规划算法。用通俗的语言来描述的话,首先我们的目标是寻找从点i到点j的最短路径。从动态规划的角度看问题,我们需要为这个目标重新做一个诠释(这个诠释正是动态规划最富创造力的精华所在)
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,我们假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当我们遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
算法步骤
a.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
b.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
inf = float('inf')
matrix_distance = [[0,1,12,inf,inf,inf],
[inf,0,9,3,inf,inf],
[inf,inf,0,inf,5,inf],
[inf,inf,4,0,13,15],
[inf,inf,inf,inf,0,4],
[inf,inf,inf,inf,inf,0]]
def Floyd(dis):
#min (Dis(i,j) , Dis(i,k) + Dis(k,j) )
nums_vertex = len(dis[0])
for k in range(nums_vertex):
for i in range(nums_vertex):
for j in range(nums_vertex):
if dis[i][j] > dis[i][k] + dis[k][j]:
dis[i][j] = dis[i][k] + dis[k][j]
return dis
print(Floyd(matrix_distance))
参考链接: