在初步学完初阶数据结构的排序后,我发现了一个非常不得了的问题。那就是,在拿出一个排序的名字时(除了几个令人印象深刻的),我根本不能第一时间想起它们的思路啊!!!这就好比上厕所时,感觉要出来但又出不来一样令人难以接受。于是我准备写一篇博客来总结一下。
目录
三数取中:(选取数组最左边数,最右边数,中间的数。三者中第二大的数)
1.冒泡排序
首先就是我们的老伙计了,相比较其他排序老伙计算是较容易实现的了。
(1)思路

思路:
从初始位置开始进行比较,也就是将arr[0]与arr[1]进行比较。如果arr[0]大于arr[1],则将两者值进行交换。然后将arr[1]与arr[2]进行比较……..依此类推。
每次比较完一轮后,就代表比较后最大的值到达了正确的位置,这时只需要将下轮要比较的总个数-1就行了。
(2)代码实现
//冒泡排序
void BubbleSort(int* arr, int n)
{
for (int i = 0; i < n; i++)
{
int flag = 0;
for (int j = 1; j < n - i; j++)//i的逐步增加实现了下轮比较总个数的减少
{
if (arr[j-1] > arr[j])
{
swap(&arr[j - 1], &arr[j]);
flag = 1;
}
}
if (0 == flag)//当比较完一轮后,flag==0,则说明数据已经有序了
break;
}
}
2.插入排序
(1)思路
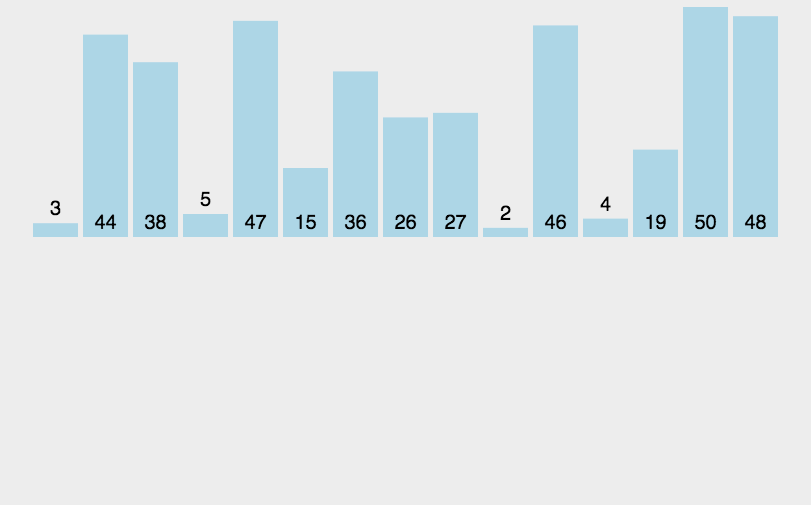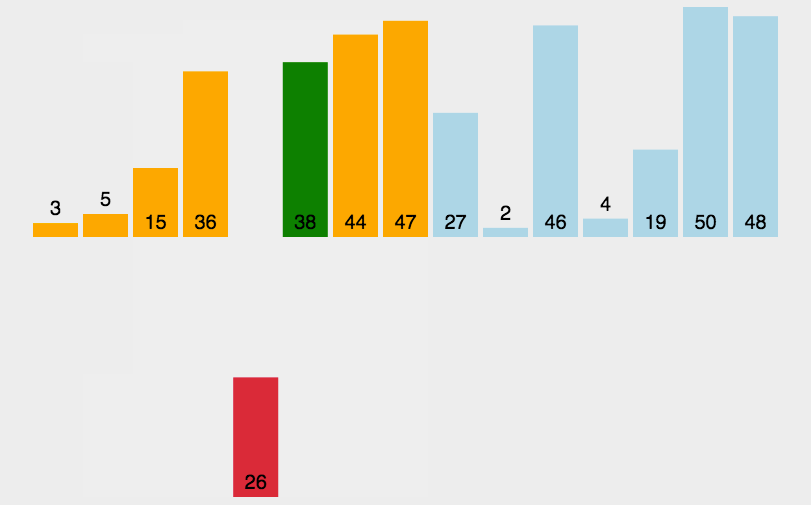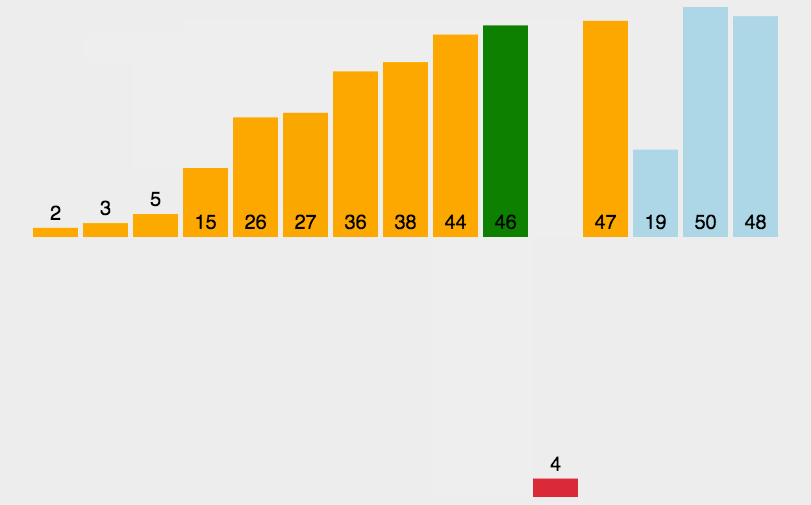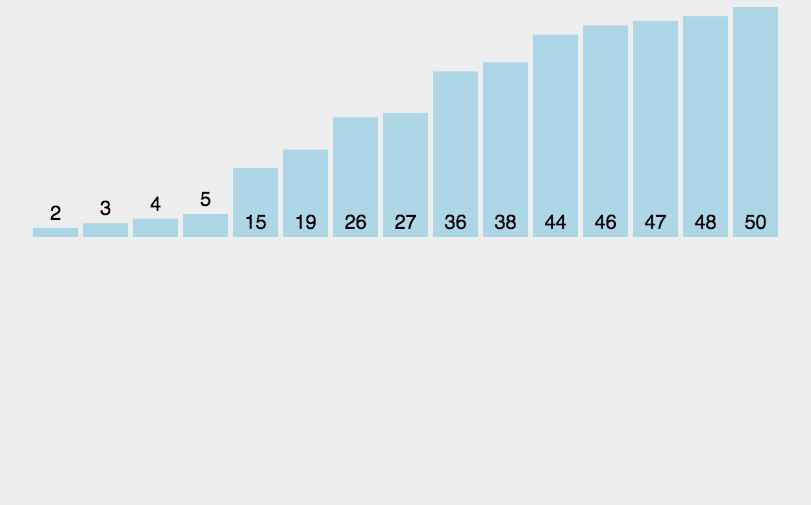
思路:插入排序就像打扑克摸牌一样,摸完一张牌后,就把它插到比它小的牌和比它大的牌中间。
也就是说,假设[0,end]区间内数据是有序的,接下来插入end+1位置的数。
令tmp = arr[end+1]。然后从arr[end]开始到arr[0]依次与tmp进行比较。(即end–,直到end<0或者.新入数据已插入,为止)。
如果tmp小,则将与tmp进行比较的数据向后“移”。
如果tmp大,则arr[end+1] = tmp。
(2)下面来举个栗子。

arr[end]与tmp比较,5>3,所以5向后移。end–.

同理4后移
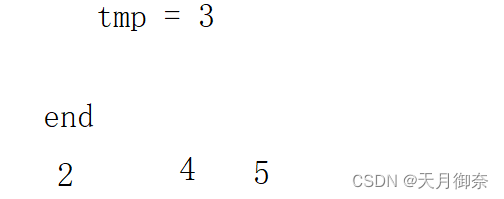
直到2<3,tmp插入,即arr[ end+1] = tmp.
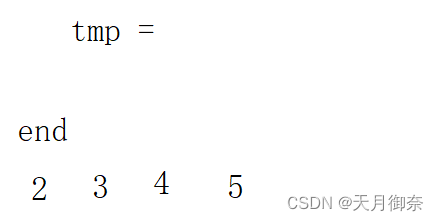
(3)代码实现
//插入排序
void insertSort(int* arr, int n)
{
for (int i = 0; i < n - 1; ++i)//多趟
{
//单趟
int end = i;
int tmp = arr[end + 1];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + 1] = arr[end];
--end;
}
else
{
break;
}
}
arr[end + 1] = tmp;
}
}
3.希尔排序
希尔排序与插入排序思路是一样的,只是希尔排序在插排的基础上加了一层优化。(预排序)
预排序的目的呢,当然就是使数据接近有序啦。
(1)思路
那,预排序到底是什么东东呢。
其实就是将间隔为gap的数据分为一组,然后进行插入排序。
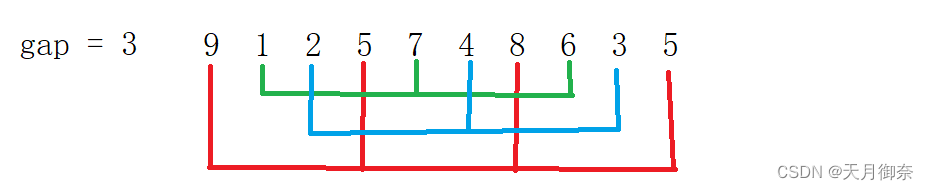
如此,较大的数据就会更快地到后面,较小的数据就会更快地到前面。
代码实现:只需要在插入排序的基础之上稍加改动就行了。
void ShellSort(int* arr, int n)
{
for (int gap = 3; gap > 0; gap--)
{
for (int j = 0; j < gap; ++j)
{
for (int i = j; i < n - gap; i += gap)
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}
}但,看着上面的代码感觉循环太多了,令人很不爽。于是就有了下面的优化。
代码优化(实现):
//希尔排序
void ShellSort(int* arr, int n)
{
int gap = n;
while(gap > 1)
{
gap = gap / 3 + 1;//使gap最终变为1
for (int i = 0; i < n - gap; i++)//gap组数据依次多组并排
{
int end = i;
int tmp = arr[end + gap];
while (end >= 0)
{
if (arr[end] > tmp)
{
arr[end + gap] = arr[end];
end -= gap;
}
else
{
break;
}
}
arr[end + gap] = tmp;
}
}
}优化思路

排完红色一组的第一个数据后,i++,去排绿组的第一个数据,再i++,去排蓝组的第一个数据,再i++,去排红组第二个数据………
4.直接选择排序
思路:
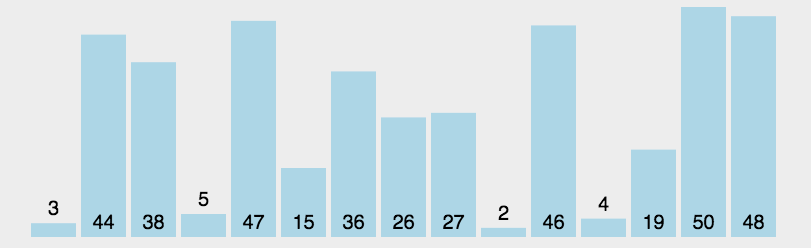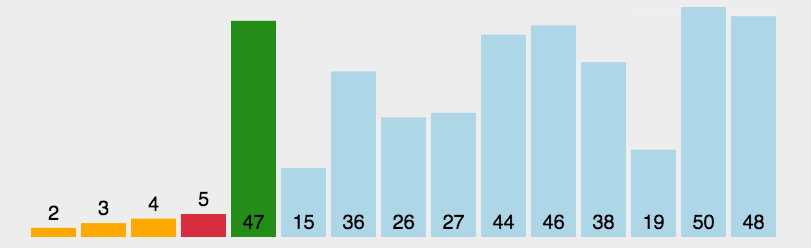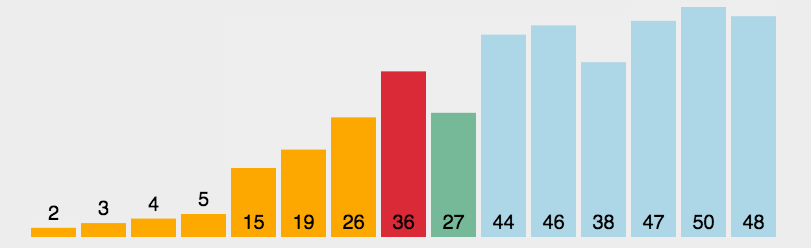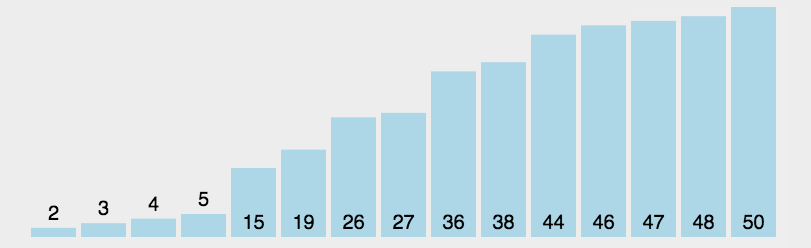
其实就是将数据一个一个一个地比较,选出最小的数据,放在最左边。既然,都选出了最小的,为什么我们不再选一个最大的放在最右边呢。这么一来,新的优化思路就出现啦!
代码实现(有bug):
void SelectSort(int* arr, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
//选出小的放begin
//选出大的放end
int max = begin, min = begin;
for (int i = begin + 1; i <= end; i++)
{
if (arr[i] < arr[min])
{
min = i;
}
if (arr[i] > arr[max])
{
max = i;
}
}
swap(&arr[begin], &arr[min]);
swap(&arr[end], &arr[max]);
++begin;
--end;
}
}上面的代码虽然已经差不多实现出来了,但是还有一个非常容易忽略的坑。就是
当最大值正好在最左侧,min与最左侧值交换后,min就变成了所谓的“最大”。导致排序出错。
这个坑只会在同时选max,min时出现,也就是在优化的思路中出现,如果只是简单地选出min放左边并不会受到影响。
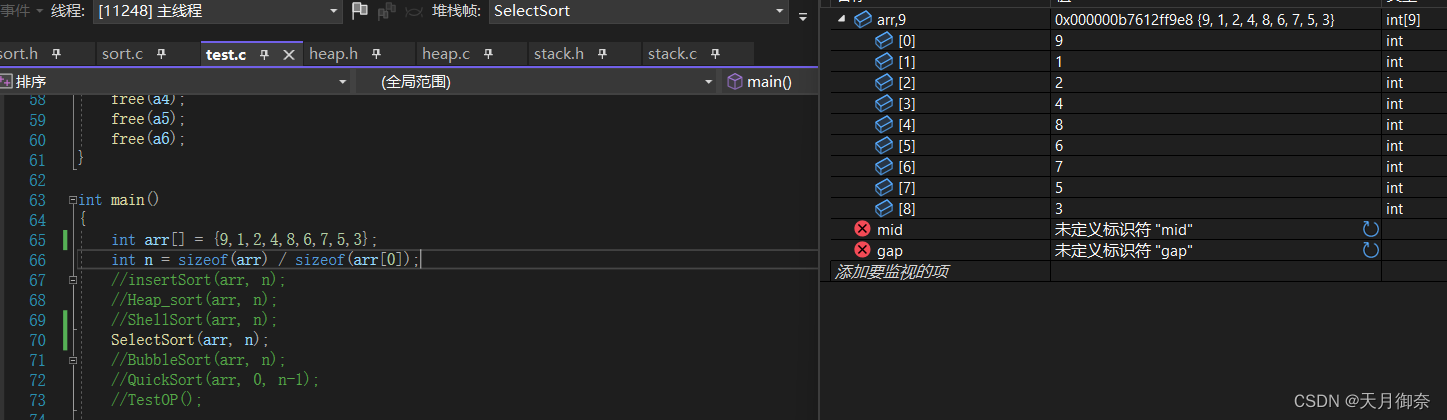
所以就需要对max进行修正。
代码实现:
//选择排序
void SelectSort(int* arr, int n)
{
int begin = 0, end = n - 1;
while (begin < end)
{
//选出小的放begin
//选出大的放end
int max = begin, min = begin;
for (int i = begin + 1; i <= end; i++)
{
if (arr[i] < arr[min])
{
min = i;
}
if (arr[i] > arr[max])
{
max = i;
}
}
swap(&arr[begin], &arr[min]);
//修正max
if (max == begin)
max = min;
swap(&arr[end], &arr[max]);
++begin;
--end;
}
}
5.堆排序
堆排序与其他的排序还是有很大不同的,并且如果要理解堆排序,最最重要的方法就是画图啦。如果不画图,那就相当于把刀扔在旁边,直接用空手去劈榴莲。为了方便手不铁的我,所以接下来我就多用画图来解释了。
思路:
思路:
刚开始的数据是无序的,所以就需要将它们建成大堆或者小堆(以下使用大堆)
我们可以把父节点与子节点比较,确保最大的数位于父节点位置。
向下调整函数:
//向下调整(确保最大的数位于父节点位置)
void Adjustdown(Type* arr, int sz, int parent)
{
int minchild = parent * 2 + 1;//初始为左孩子
while (minchild < sz)
{
//取左右孩子中最大的
if (arr[minchild] < arr[minchild + 1] && minchild + 1 < sz)
{
minchild++;//变为右孩子
}
if (arr[minchild] > arr[parent])
{
swap(&arr[parent], &arr[minchild]);
parent = minchild;
minchild = parent * 2 + 1;
}
else
{
break;
}
}
}
因为叶子节点本身就是一个天然的堆,所以,只需要从倒数第一个非叶子节点(最后一个节点的父亲)开始调整。
//建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)//倒数第一个非叶子节点(最后一个节点的父亲)开始调整
{ //由child = parent*2+1 推出parent = (child-1)/2 即 (n-1 -1)/2
Adjustdown(arr, n, i);
}以下一组数据{9,1,2,4,8,6,7,5,3}为例。
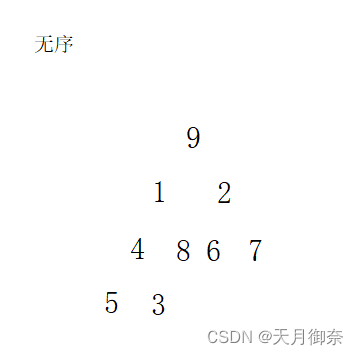
(1)i = (n-1 -1)/2 = 3,所以将arr[3]与子节点比较,即4与5,3比较。因为5>4,所以4与5交换位置。

(2)i–, 所以将arr[2]与子节点比较,即2与6,7比较。因为7>6>2,所以2与7交换位置。
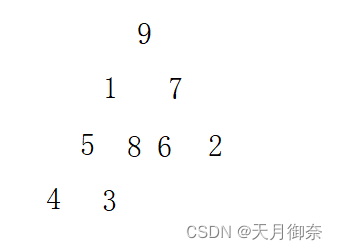
(3)同理,得到以下结果。

这么一来,大堆就建好啦。
然后是选数,将根节点位置的数与最后的叶子节点交换,再进行向下调整,确保根节点位置数在剩下的数中最大,最后size–,让最后一个排好的数不进入之后的排序。
每次交换使得最大的数到达正确的位置,如此反复,堆排序就完成啦!
//选数
int i = 1;
while (i < n)
{
swap(&arr[0], &arr[n - i]);//每次交换使得最大的数到达正确的位置
Adjustdown(arr, n - i, 0);
i++;
}
画图举例:
交换根节点位置的数与最后叶子节点位置的数

向下调整

交换根节点位置的数与最后叶子节点位置的数

向下调整

交换根节点位置的数与最后叶子节点位置的数

向下调整

依此类推

最终实现堆排序
代码实现:
//堆排序
void Heap_sort(int* arr, int n)
{
//建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)//倒数第一个非叶子节点(最后一个节点的父亲)开始调整
{ //由child = parent*2+1 推出parent = (child-1)/2 即 (n-1 -1)/2
Adjustdown(arr, n, i);
}
//选数
int i = 1;
while (i < n)
{
swap(&arr[0], &arr[n - i]);//每次交换使得最大的数到达正确的位置
Adjustdown(arr, n - i, 0);
i++;
}
}
6.快速排序
从名字可以看出来,快速排序的主要特点就是,快!
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,之后又有一些大佬对其进行了优化,还有一些大佬又用别的思路将它实现了。所以,接下来有三种不同版本的快排实现思路。(啊啊啊,写死我啦)
1,hoare版本
思路:
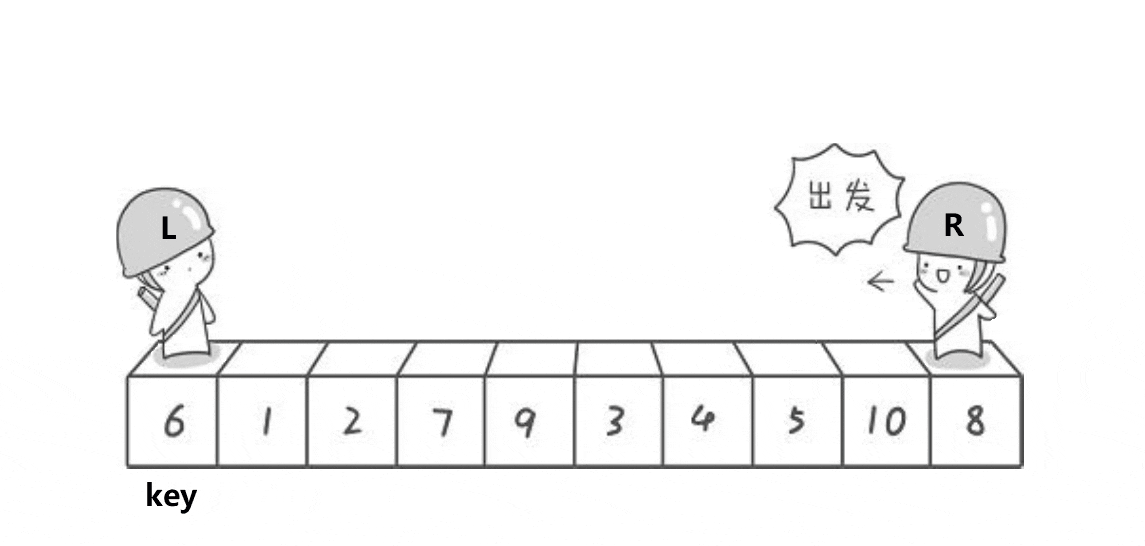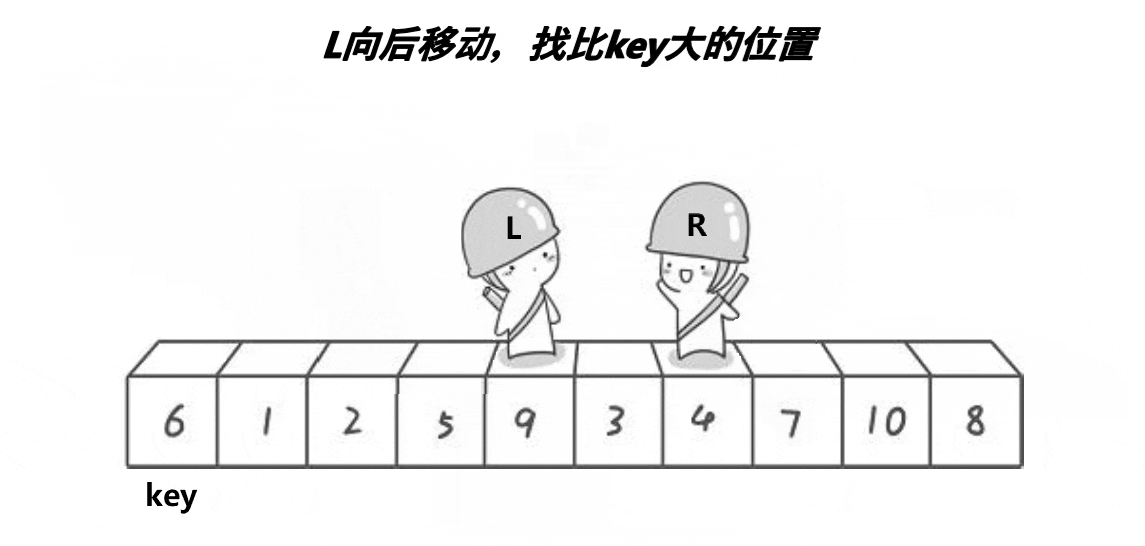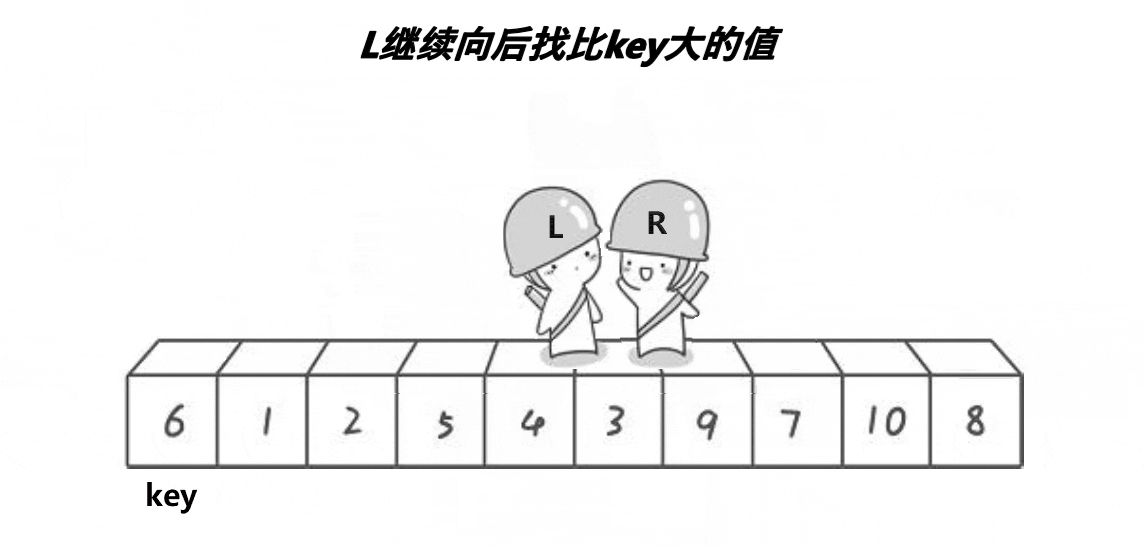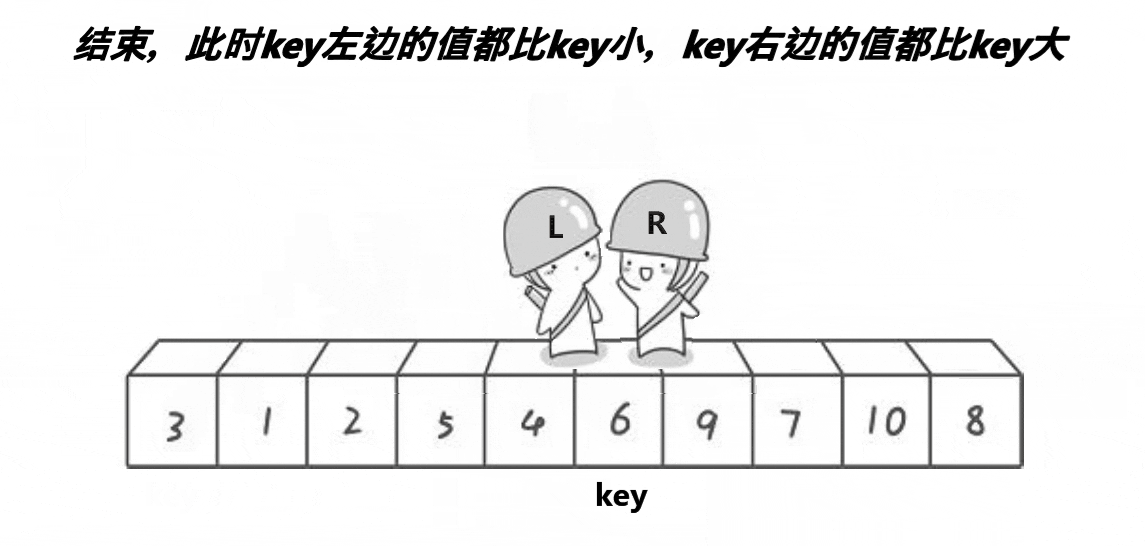
总的来说就是,R找比key小的数,找到之后,R不动。
L开始行动找比key大的数,找到后,交换两数位置,R继续行动……两者相遇后将相遇位置的值与key交换。
如此,6左边全是比6小的数,右边全是比6大的数。(以图中为例)即,6到达最终的位置。再用递归来实现快排(在最后快排主体)。
因为考虑到代码效率的问题,key使用三数取中的方法来选取的效率,比直接key=arr[0]的效率高。所以,下面我就使用三数取中了哦。
三数取中:(选取数组最左边数,最右边数,中间的数。三者中第二大的数)
//三数取中
int GetMidIndex(int* arr, int left, int right)
{
int mid = (right + left) / 2;
if (arr[mid] > arr[left])
{
if (arr[mid] < arr[right])
{
return mid;
}
else if (arr[left] > arr[right])
{
return left;
}
else
{
return right;
}
}
else
{
if (arr[mid] > arr[right])
{
return mid;
}
else if (arr[left] < arr[right])
{
return left;
}
else
{
return right;
}
}
}代码实现:
//快速排序hoare版本[left,right]
int PartSort1(int* arr, int left, int right)
{
//三数取中
int mid = GetMidIndex(arr, left, right);
swap(&arr[mid], &arr[left]);
int keyi = left;
while (left < right)
{
//R找小
while (left < right && arr[right] >= arr[keyi])//因为right在变化,所以要时时刻刻判断left<right
{
--right;
}
//L找大
while (left < right && arr[left] <= arr[keyi])//因为left在变化,所以要时时刻刻判断left<right
{
++left;
}
if (left < right)
swap(&arr[left], &arr[right]);
}
swap(&arr[left], &arr[keyi]);
//返回相遇点
return left;
}
2,挖坑法
思路:
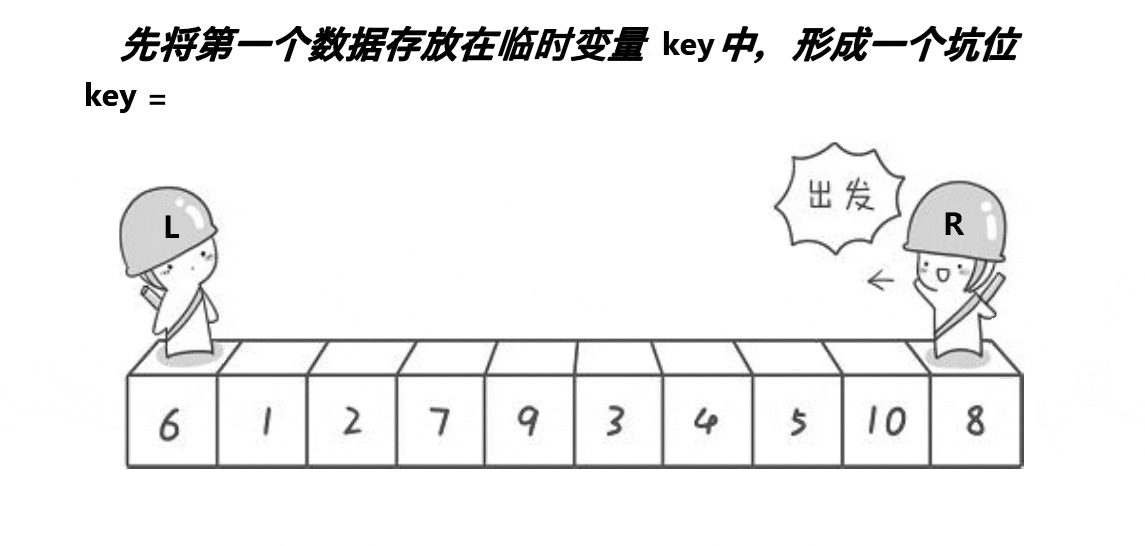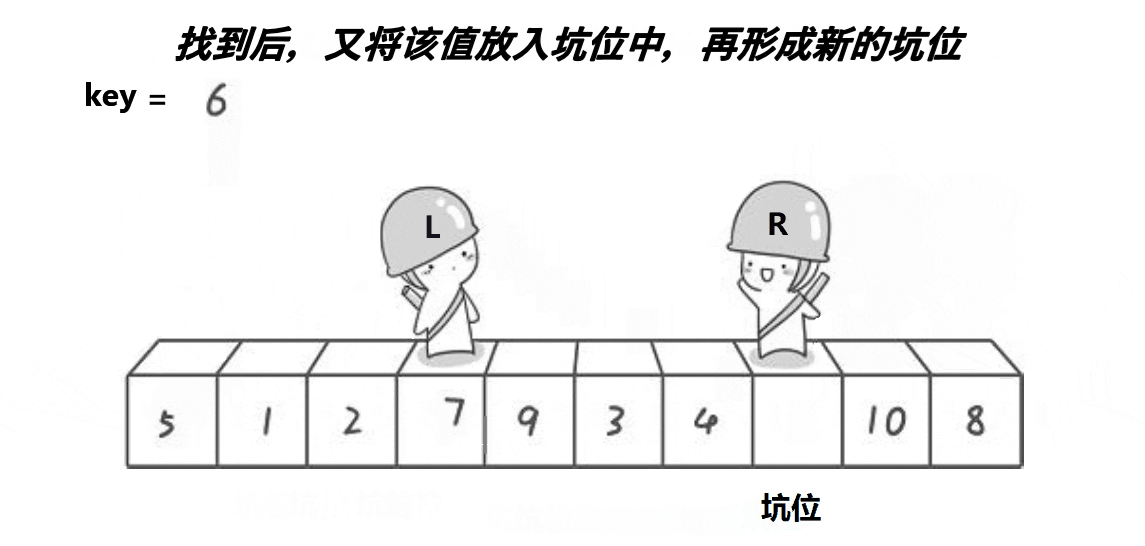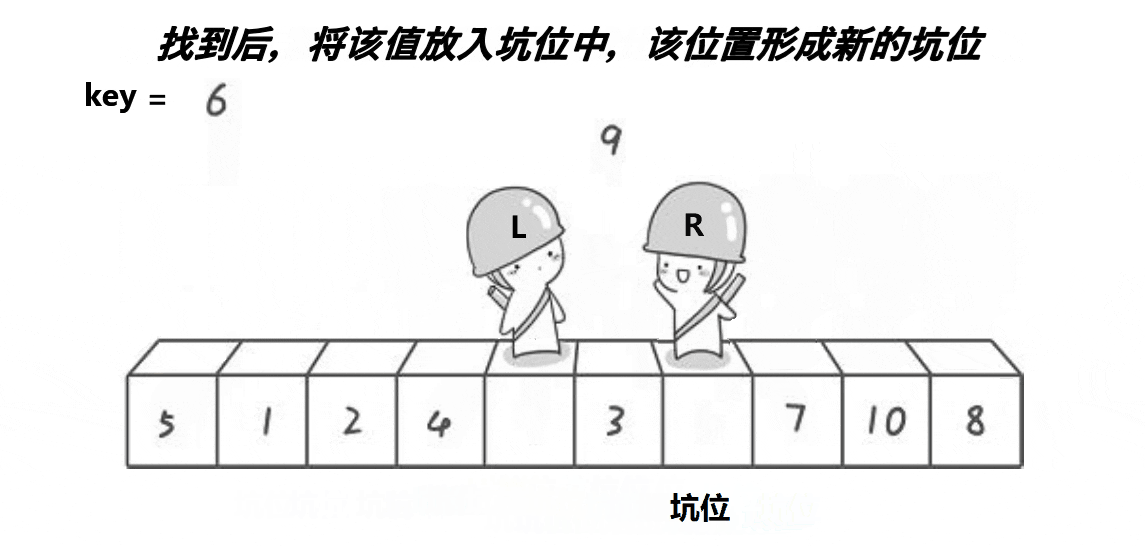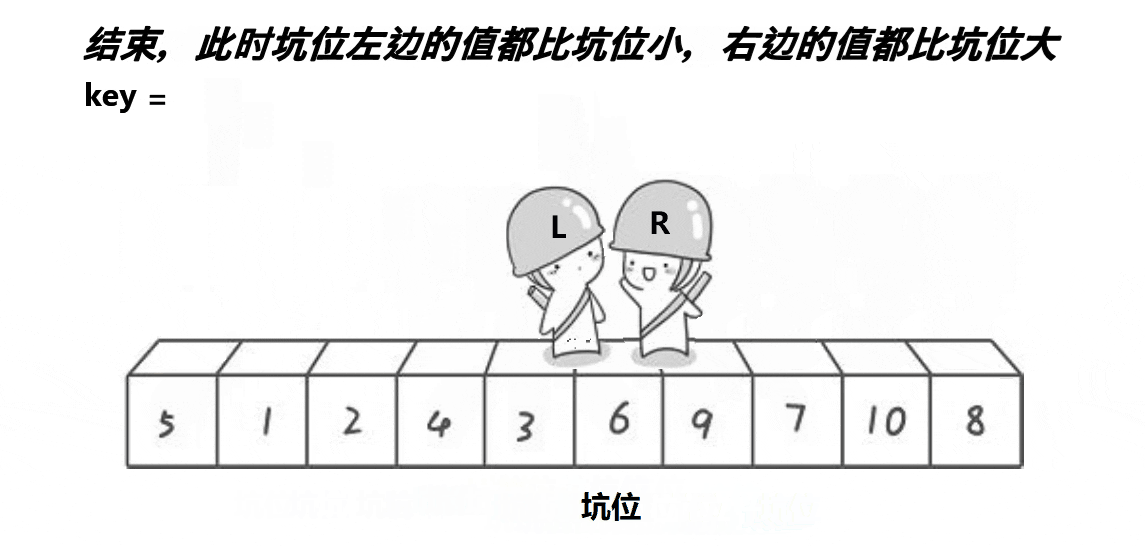
挖坑法的思路与 hoare版本是相似的,R找比key大的数,填到左边的坑,形成新的坑位
,
然后L行动,找比key小的数,填到右边的坑,形成新坑位
……
两者相遇后,把key填入相遇点。
代码实现:
int PartSort2(int* arr, int left, int right)
{
// 三数取中
int mid = GetMidIndex(arr, left, right);
swap(&arr[left], &arr[mid]);
int key = arr[left];
int hole = left;
while (left<right)
{
//右边找大,填左坑
while (left < right && arr[right] >= key)//因为right在变化,所以要时时刻刻判断left<right
{
--right;
}
arr[hole] = arr[right];
hole = right;
//左边找小,填右坑
while (left < right && arr[left] <= key)因为left在变化,所以要时时刻刻判断left<right
{
++left;
}
arr[hole] = arr[left];
hole = left;
}
arr[hole] = key;
//返回相遇点
return hole;
}
3,前后指针法
思路:
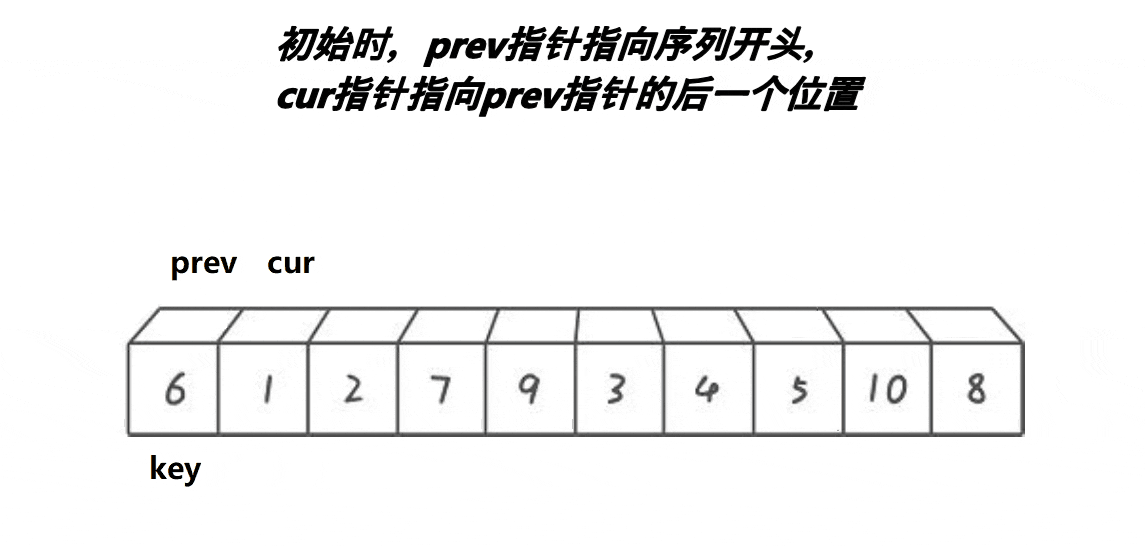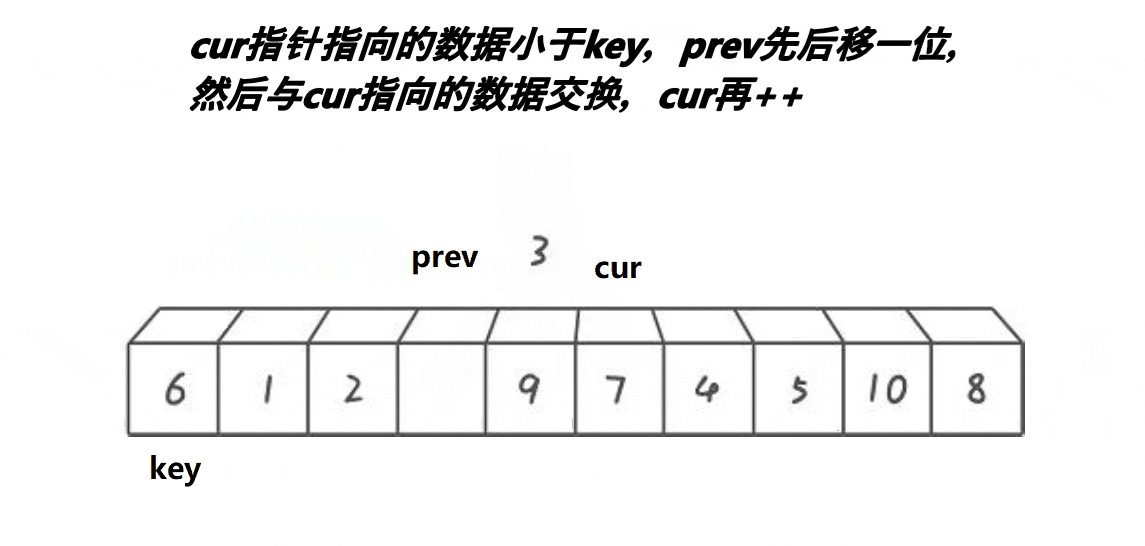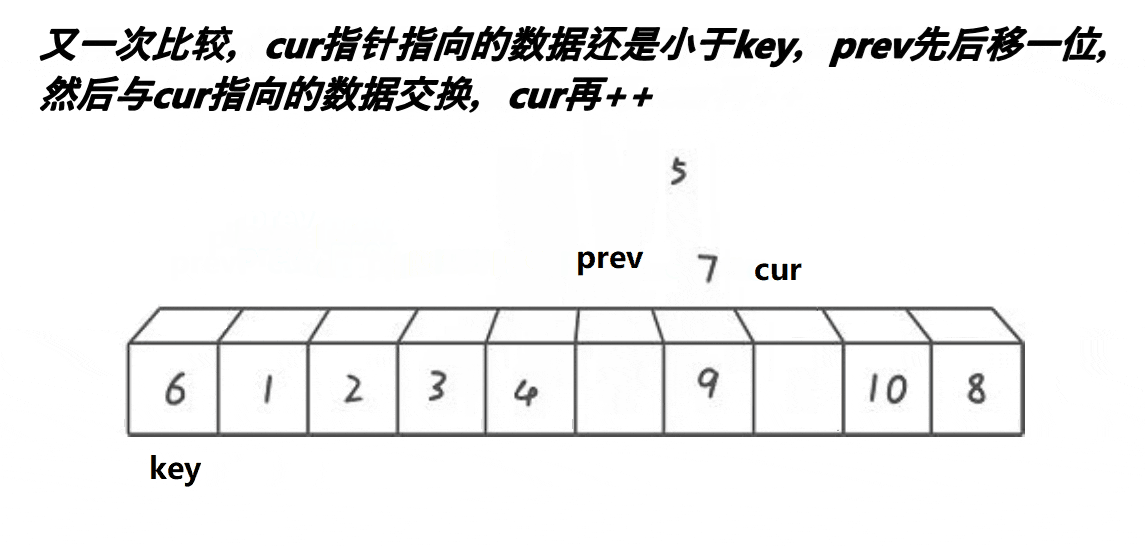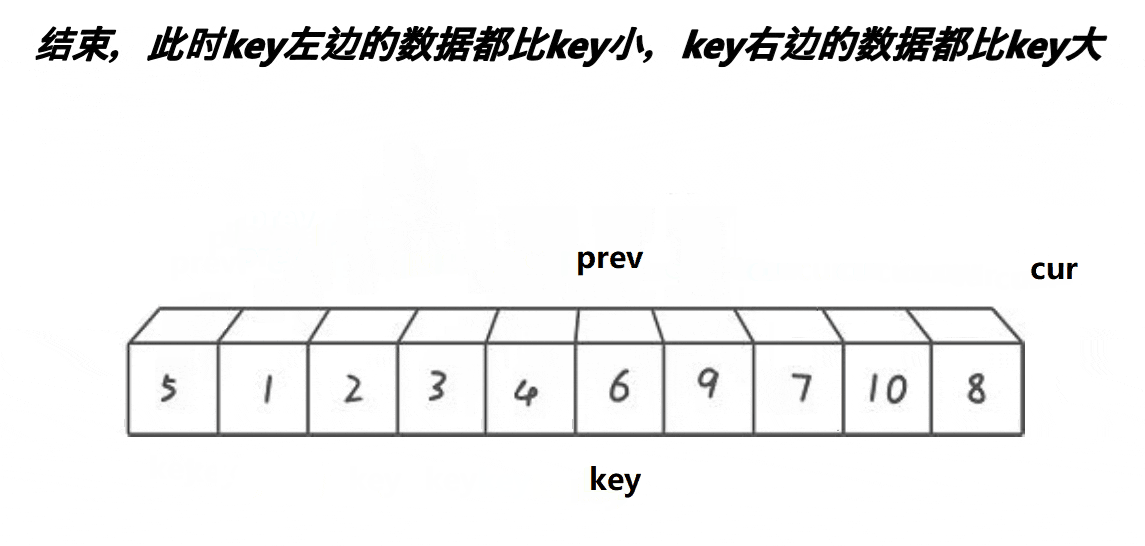
初始时,prev指针指向序列开头,cur指针指向prev指针的后一个位置。
然后判断cur指针指向的数是否小于key,若小于,则prev指针后移一位,cur指向的内容与prev指向的内容交换(prev与cur在同一位置时不变),然后cur++。
若大于,直接cur++。
当cur越界时将prev指向内容与key进行交换。
代码实现:
// 快速排序前后指针法
int PartSort3(int* a, int left, int right)
{
// 三数取中
int mid = GetMidIndex(a, left, right);
swap(&a[left], &a[mid]);
int key = a[left];
int prev = left;
int cur = left + 1;
//cur找小,prev紧跟
while (prev <= cur)
{
//cur甩开prev后,并遇到小时交换
if (a[cur] < key && ++prev != cur)
{
swap(&a[prev], &a[cur]);
}
++cur;
}
swap(&a[left], a[prev]);
return prev;
}
快速排序主体(递归实现)
思路:
首先对初始数组排序使6到达最终位置
,
再对6的左边数组进行排序使3到达最终位置
,
再对6右边数组进行排序使8到达最终位置
。再对3左边数组………最终实现有序。(二叉树结构)
//快速排序[begin,end]
void QuickSort(int* arr, int begin, int end)
{
//为空或只有一个时返回
if (begin >= end)
return;
if (end - begin <= 8)
{
insertSort(arr + begin, end - begin + 1);//当数组较小时,使用插入排序,提高效率
}
else
{
int keyi = PartSort1(arr, begin, end);//以上三种方法任选一个
//左
QuickSort(arr, begin, keyi - 1);
//右
QuickSort(arr, keyi + 1, end);
}
}
7.归并排序
思路(图解):
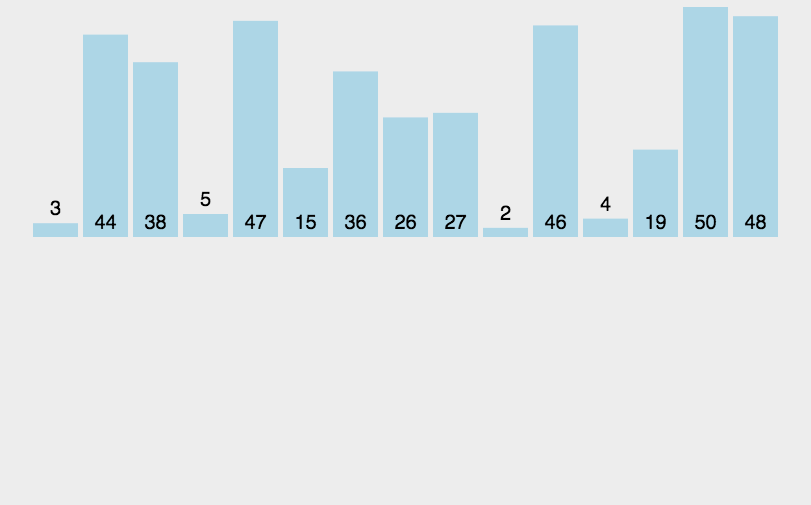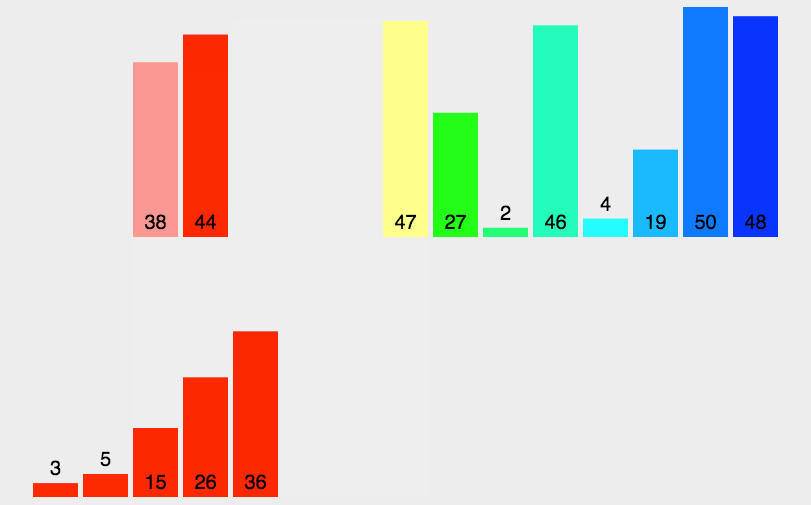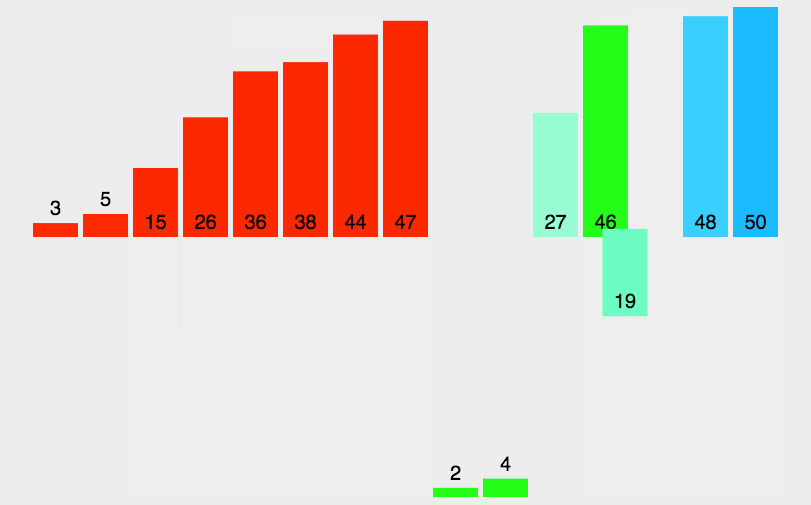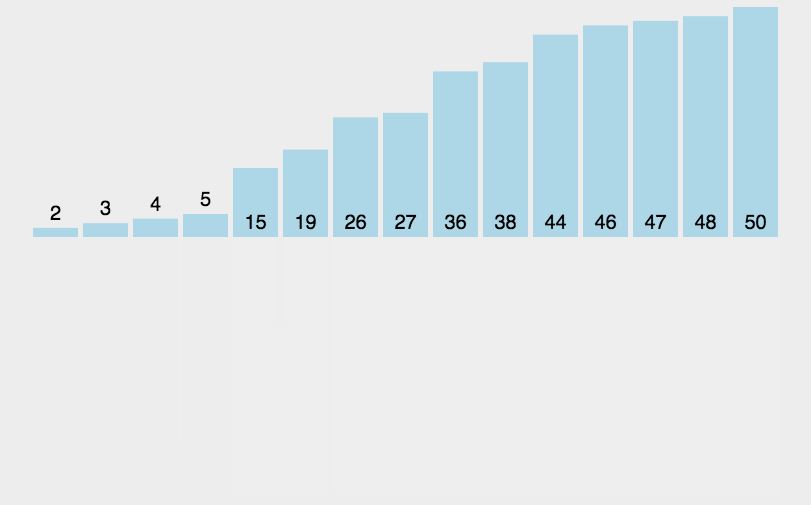
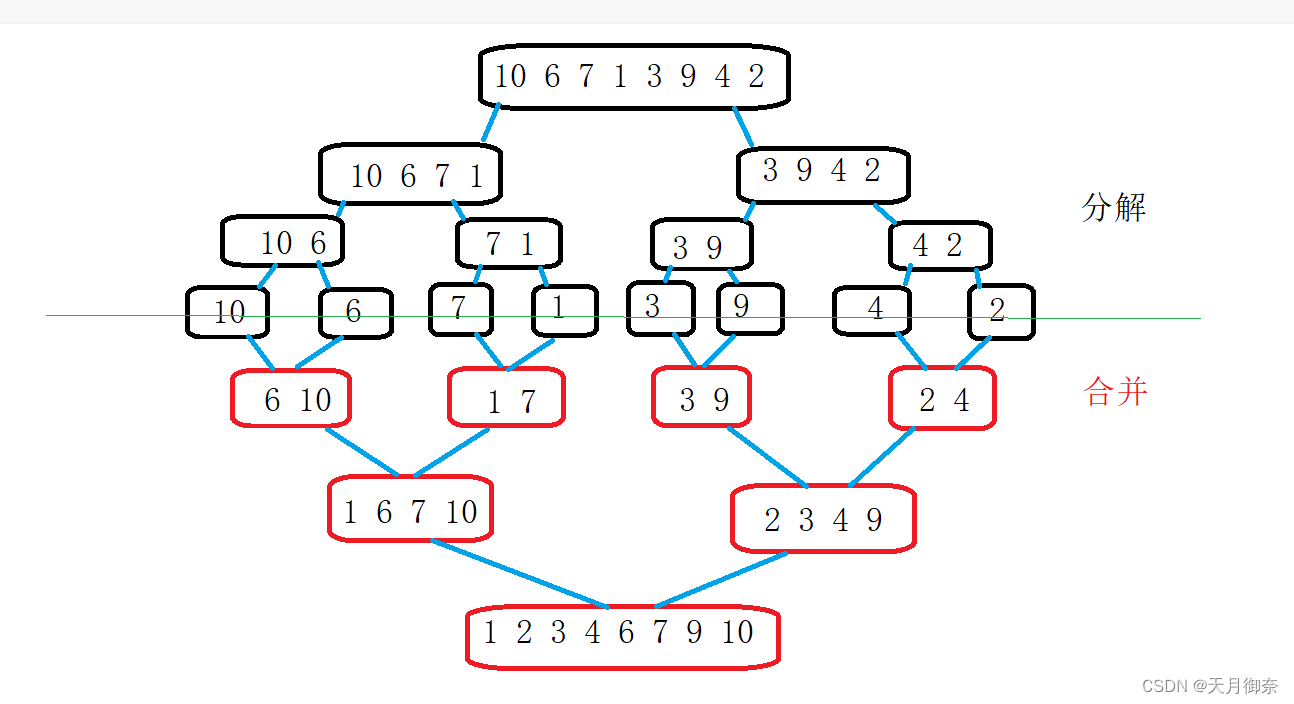
代码实现:
//归并排序
void mergeSort(int* arr, int begin, int end, int* tmp)
{
//分解
//数组中数据个数为1或者0时返回
if (begin >= end)
return;
int mid = (begin + end) / 2;
//左
mergeSort(arr, begin, mid, tmp);
//右
mergeSort(arr, mid + 1, end, tmp);
//合并
int begin1 = begin, end1 = mid;
int begin2 = mid + 1, end2 = end;
int i = begin;
//将小的放入tmp数组
while (begin1 <= end1 && begin2 <= end2)
{
if (arr[begin1] <= arr[begin2])
tmp[i++] = arr[begin1++];
else
tmp[i++] = arr[begin2++];
}
//将大的尾插到tmp数组
while (begin1 <= end1)
{
tmp[i++] = arr[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = arr[begin2++];
}
//将tmp拷贝回原来数组
memcpy(arr + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}
void MergeSort(int* arr, int n)
{
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc");
return;
}
mergeSort(arr, 0, n - 1, tmp);
free(tmp);
tmp = NULL;
}
啊!!!终于写完啦,最后写地脑壳疼·,如果大家发现了我哪里写错了欢迎斧正哦!文中动图来源于网络。
欧拉欧拉欧拉欧拉欧拉欧拉欧拉欧拉欧拉欧拉!!!!!
木大木大木大木大木大木大木大木大木大木大!!!!!