博客

第十一章 方差分析表（analysis of variance table）ANOVA TABLE

  • Post author:
  • Post category:其他


11.1 方差分析表概念

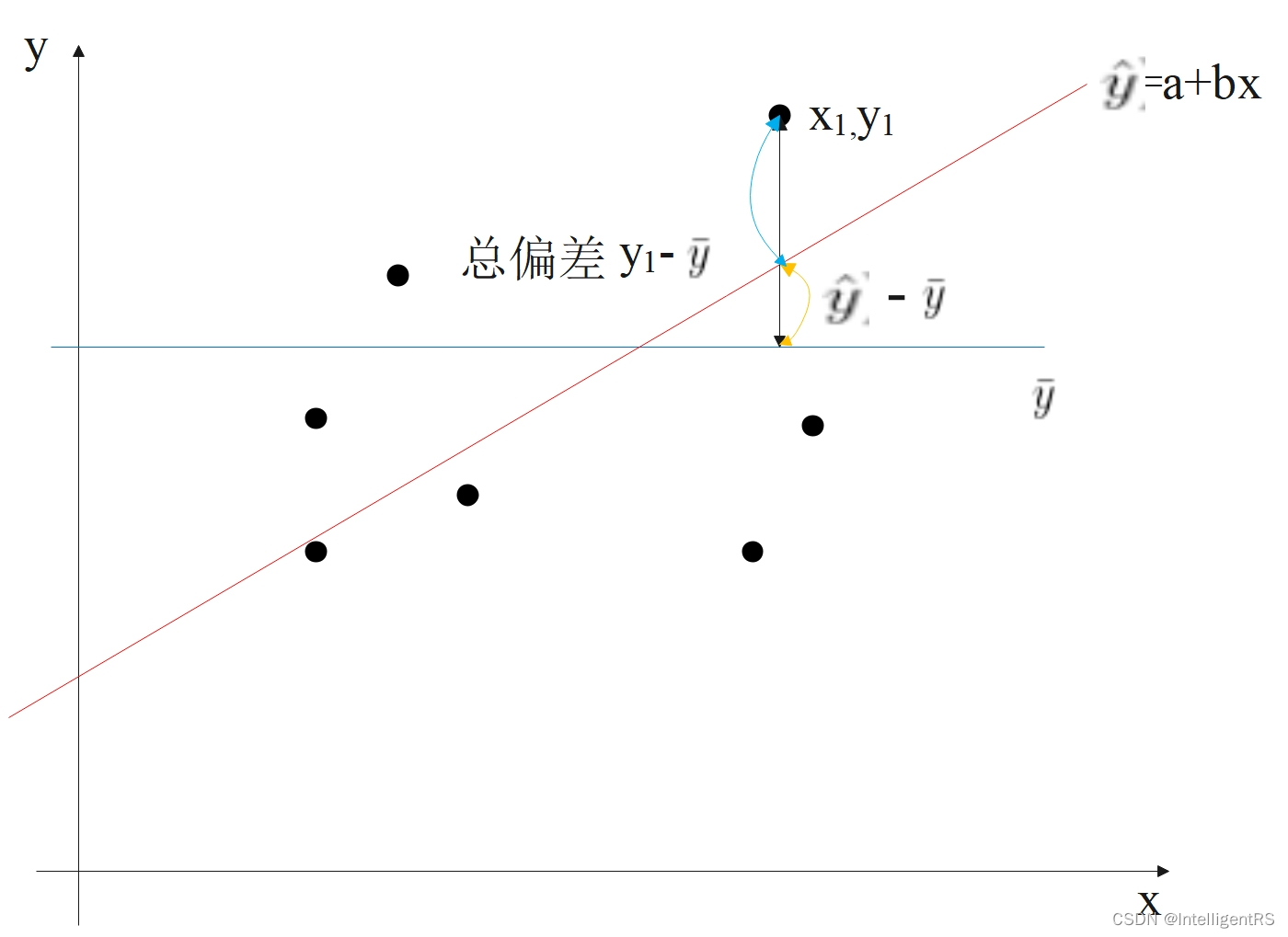
回归平方和：SSR(Sum of Squares for regression) = ESS (explained sum of squares)

残差平方和：SSE（Sum of Squares for Error） = RSS (residual sum of squares)

总离差平方和：SST(Sum of Squares for total) = TSS(total sum of squares)


SSE+SSR=SST RSS+ESS=TSS

TSS = (Y_1-\overline{Y})^2+(Y_2-\overline{Y})^2+(Y_3-\overline{Y})^2+......

RSS = (\hat{Y_1}-\overline{Y})^2 + (\hat{Y_2}-\overline{Y})^2+(\hat{Y_3}-\overline{Y})^2+......

SSE = (y_1-\hat{y})^2+(y_2-\hat{y})^2+ (y_3-\hat{y})^2+......=(e_1)^2+(e_2)^2+(e_3)^2+......

TSS = SSE + RSS

R^2
（决定系数 Coefficient of Determination）:

(1)R^2 = \frac{RSS(Explained\;Variation)}{TSS(Total\;Variation)} = 1-\frac{SSE(Unexplained\;Variation)}{TSS(Total\;Variation)}
(2)0\leq R^2\leq 1\;R^2
越接近于1，解释力度越大

(3)R^2=r^2

SEE(Standard Error of Estimate):

Actual Y – Estimated Y

SEE = \sqrt{\frac{SSE}{n-2}}=\sqrt{MSE}

SEE = \sqrt{\frac{(e_1-\bar{e})^2+(e_2-\bar{e})^2+(e_3-\bar{e})^2+......}{n-k-1}}

SSE = (y_1-\hat{y})^2+(y_2-\hat{y})^2+(y_3-\hat{y})^2+......=(e_1)^2+(e_2)^2+(e_3)^2+......

而此时，
\bar{e}
为一个垃圾桶，均值为0。

11.2 检验

11.2.1 T检验

（1）点估计（point estimation）
C=100*H+88\;--->H->\hat{b_1}\;88->\hat{b_0}

（2）置信区间（Confident Interval）
b_1\;95%\;b_1(\hat{b_1}\pm 1.96S_{\hat{b_1}})

S_{\hat{b_1}
如果增大，SEE相应上升，因为本质上SEE是描述数据的波动性（variability of data）


检验方法：假设检验

（1）

H_0:b_1=0

H_a:b_1\neq0

（2）

t=\frac{\hat{b_1}-0}{S_{\hat{b_1}}}

（3）画图判断

（4）结论：b1 is significantly different from 0

（5）不一定要与0进行判断

11.2.2 F-检验（联合检验）

Y = b_0+b_1*1+b_2*2+b_3*3+......+b_k*k+\varepsilon

（1）

H_0:b_1=b_2=b_3=......=0

H_a
至少有一个
b_i\neq0

（2）

F=\frac{RSS/k}{SSE/(n-k-1)}


版权声明：本文为qq_36171491原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。