相关资料
广州大学机器学习与数据挖掘实验一:线性回归
广州大学机器学习与数据挖掘实验二:决策树算法
广州大学机器学习与数据挖掘实验三:图像分类
广州大学机器学习与数据挖掘实验四:Apriori算法
四份实验报告
下载链接?
一、实验目的
本实验课程是计算机、智能、物联网等专业学生的一门专业课程,通过实验,帮助学生更好地掌握数据挖掘相关概念、技术、原理、应用等;通过实验提高学生编写实验报告、总结实验结果的能力;使学生对机器学习算法、数据挖掘实现等有比较深入的认识。
1.掌握机器学习中涉及的相关概念、算法。
2.熟悉数据挖掘中的具体编程方法;
3.掌握问题表示、求解及编程实现。
二、基本要求
1.实验前,复习《机器学习与数据挖掘》课程中的有关内容。
2.准备好实验数据。
3.编程要独立完成,程序应加适当的注释。
4.完成实验报告。
三、实验软件
使用Python或R语言实现。
四、实验内容
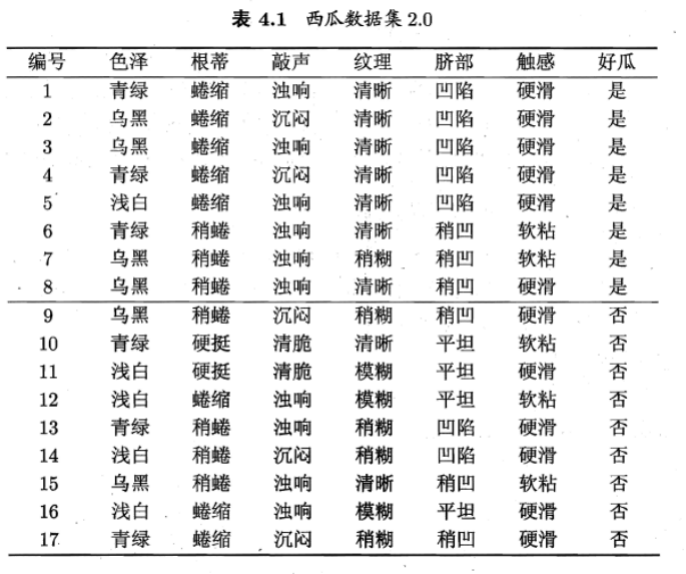
表4.1的西瓜数据集包括17个训练样例,请学习一个决策树,用于预测一个西瓜是不是好瓜。具体要求如下:
(1)在生成决策树的过程中,请分别使用ID3算法、C4.5算法、CART算法,并对比三个算法结果。其中,,ID3算法在生成决策树的各结点使用信息增益准则进行特征选择;C4.5算法在生成决策树的过程使用信息增益比进行特征选择;CART算法假设决策树是一个二叉树通过递归地二分每个特征,将特征空间划分为有限个单元,并在这些单元上确定预测的概率分布。
(2)请自己写程序实现决策树的生成过程,不要直接调用决策树算法包。
五、实验过程
三个算法均以数据结构——树相关,因此可以采用递归算法进行生成决策树,对于输入数据分别按照信息增益、信息增益比、基尼指数去进行多分类或二分类,然后递归调用划分子树算法,最终生成一颗决策树。
对于ID3算法,我们选择信息增益去选择划分特征;
对于C4.5算法,我们选择信息增益比去选择划分特征;
对于CART算法,我们选择基尼指数去选择细粒度更低的特征内的属性去进行二分类划分,比如纹理是否清晰等等。
六、实验结果与评估
ID3算法可视化如下:
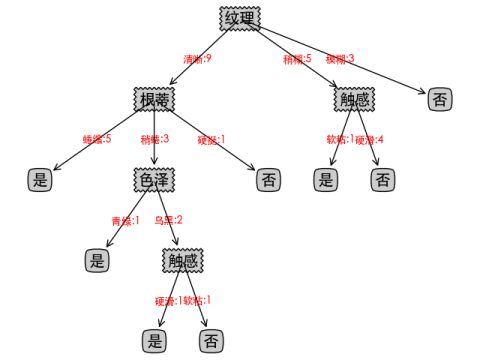
C4.5算法可视化如下:
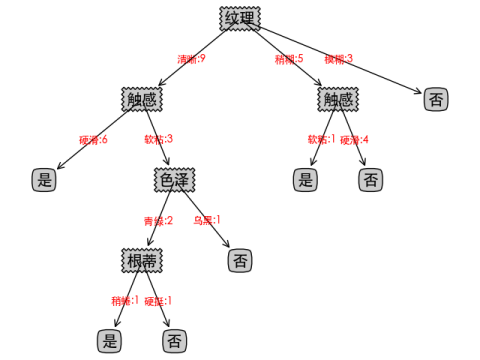
CART算法可视化如下:
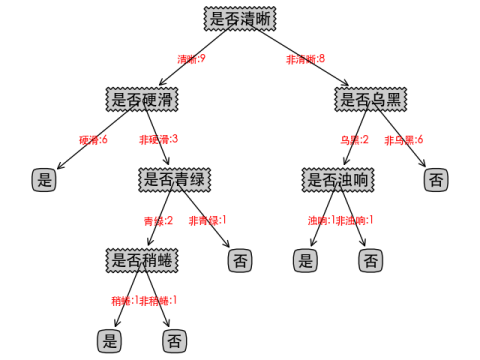
| 决策树算法 | 特征选择 | 是否二叉树 | 非叶子节点 | 叶子节点 |
|---|---|---|---|---|
| ID3 | 信息增益 | 否 | 5 | 8 |
| C4.5 | 信息增益比 | 否 | 5 | 7 |
| CART | 基尼指数 | 是 | 6 | 7 |
评价:
1、三种算法由于特征选择的度量不同,可视化出来的决策树也不一样,而且决策树深度由于样本数量不多保持一致,均都是5。
2、可以看到CART由于使用的是二叉树,非叶子节点会多于其他两个算法。
3、非叶子节点的个数可以反映该决策树是否容易过拟合,非叶子节点个数越多的决策树越容易过拟合,这里也可以看出CART和C4.5要略优于ID3算法,但样本数量不多,不能准确下定论。
4、额外的拓展,CART全称分类和回归树,二叉树的特性可以让它不仅适用于分类问题,也可用于回归问题。
七、实验代码
from math import log2
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.font_manager import FontProperties
# 计算标签出现次数
def get_counts(data):
total = len(data)
results = {}
for d in data:
results[d[-1]] = results.get(d[-1], 0) + 1
return results, total
# 计算信息熵
def calcu_entropy(data):
results, total = get_counts(data)
ent = sum([-1.0 * v / total * log2(v / total) for v in results.values()])
return ent # 熵
# ID3算法,计算每个feature的信息增益
def calcu_each_gain(column, update_data):
total = len(column)
grouped = update_data.iloc[:, -1].groupby(by=column)
temp = sum([len(g[1]) / total * calcu_entropy(g[1]) for g in list(grouped)])
return calcu_entropy(update_data.iloc[:, -1]) - temp #熵-条件熵
# C4.5算法,计算每个feature的信息增益率
def calcu_each_gain_rate(column, update_data):
total = len(column)
grouped = update_data.iloc[:, -1].groupby(by=column) #分组
temp = sum([len(g[1]) / total * calcu_entropy(g[1]) for g in list(grouped)])
H_a = -1*sum(len(g[1])/total * log2(len(g[1])/total) for g in list(grouped)) #惩罚参数
gain_rate = (calcu_entropy(update_data.iloc[:, -1]) -temp) / H_a
return gain_rate #(熵-条件熵)/惩罚参数
# CART算法,计算每个feature内每个取值的基尼系数
def calcu_each_Gini_value(name, update_data):
column_count = dict([(ds, list(pd.unique(update_data[ds]))) for ds in update_data.iloc[:, :-1].columns])
column_name = ''
for key, value in zip(column_count.keys(), column_count.values()):
if name in value:
column_name = key
break
grouped = update_data.iloc[:, -1].groupby(by=update_data[column_name]) #分组
first_group = [g for g in list(grouped) if g[0]==name]
first_group = list(first_group[0][1])
second_group = []
[second_group.extend(g[1]) for g in list(grouped) if g[0] != name]
a = first_group.count('是')
len1 = len(first_group)
b = second_group.count('是')
len2 = len(second_group)
lens = len1+len2
if(len2 == 0):return len1 /lens *(2* a/len1*(1-a/len1))
if (len1 == 0): return len2 / lens*(2*b/len2*(1-b/len2))
return len1 /lens *(2* a/len1*(1-a/len1)) + len2 / lens*(2*b/len2*(1-b/len2))
# 获取最大的信息增益、信息增益率或最小的基尼系数的feature
def get_max_gain(temp_data,al_name):
if al_name == 'ID3':
columns_entropy = [(col, calcu_each_gain(temp_data[col], temp_data)) for col in temp_data.iloc[:, :-1]] #ID3算法:信息增益
columns_entropy = sorted(columns_entropy, key=lambda f: f[1], reverse=True)
elif al_name == 'C4.5':
columns_entropy = [(col, calcu_each_gain_rate(temp_data[col], temp_data)) for col in temp_data.iloc[:, :-1]] #C4.5算法:信息增益率
columns_entropy = sorted(columns_entropy, key=lambda f: f[1], reverse=True)
elif al_name == 'CART':
att_cat = []
[att_cat.extend(list(pd.unique(temp_data[ds]))) for ds in temp_data.iloc[:, :-1].columns]
columns_entropy = [(col, calcu_each_Gini_value(col, temp_data)) for col in att_cat]
columns_entropy = sorted(columns_entropy, key=lambda f: f[1], reverse=False)
print(columns_entropy)
return columns_entropy[0]
# 去掉数据中已存在的列属性内容,在CART树中需要注意
def drop_exist_feature(data, best_feature, al_name,inner_feature=""):
if al_name =='CART':
new_data = data[data[best_feature] == inner_feature]
inner_data = data[data[best_feature] != inner_feature]
new_data = new_data.drop(best_feature, axis=1)
new_data = [(inner_feature , new_data ),("非"+inner_feature ,inner_data )]
else:
attr = pd.unique(data[best_feature])
new_data = [(nd, data[data[best_feature] == nd]) for nd in attr]
new_data = [(n[0], n[1].drop([best_feature], axis=1)) for n in new_data]
return new_data
# 获得出现最多的label
def get_most_label(label_list):
label_dict = {}
for l in label_list:
label_dict[l] = label_dict.get(l, 0) + 1
sorted_label = sorted(label_dict.items(), key=lambda ll: ll[1], reverse=True)
return sorted_label[0][0]
# 创建决策树
def create_tree(data_set, column_count,al_name):
label_list = data_set.iloc[:, -1] #获得标签
if len(pd.unique(label_list)) == 1: #终止条件,全部为一类,返回标签
return label_list.values[0]
if all([len(pd.unique(data_set[i])) == 1 for i in data_set.iloc[:, :-1].columns]): #终止条件,类别属性全部为一类,返回标签同属一类最多的标签
return get_most_label(label_list)
best_attr = get_max_gain(data_set,al_name)[0] #获得最大收益对应的属性名
if al_name == 'CART':
column_name = ''
for key, value in zip(column_count.keys(), column_count.values()):
if best_attr in value:
column_name = key
break
tree = {'是否' + best_attr: {}}
for item in drop_exist_feature(data_set, column_name,al_name,best_attr):
tree['是否' + best_attr][item[0]+':'+str(item[1].shape[0])] = create_tree(item[1], column_count,al_name)
else:
tree = {best_attr: {}}
for item in drop_exist_feature(data_set, best_attr,al_name):
tree[best_attr][item[0]+':'+str(item[1].shape[0])] = create_tree(item[1], column_count,al_name)
return tree
# 获取树的叶子节点数目
def get_num_leafs(decision_tree):
num_leafs = 0
first_str = next(iter(decision_tree))
second_dict = decision_tree[first_str]
for k in second_dict.keys():
if isinstance(second_dict[k], dict):
num_leafs += get_num_leafs(second_dict[k])
else:
num_leafs += 1
return num_leafs
# 获取树的深度
def get_tree_depth(decision_tree):
max_depth = 0
first_str = next(iter(decision_tree))
second_dict = decision_tree[first_str]
for k in second_dict.keys():
if isinstance(second_dict[k], dict):
this_depth = 1 + get_tree_depth(second_dict[k])
else:
this_depth = 1
if this_depth > max_depth:
max_depth = this_depth
return max_depth
# 绘制节点
def plot_node(node_txt, center_pt, parent_pt, node_type):
arrow_args = dict(arrowstyle='<-')
font = FontProperties(fname=r"/System/Library/Fonts/STHeiti Medium.ttc", size=15)
create_plot.ax1.annotate(node_txt, xy=parent_pt, xycoords='axes fraction', xytext=center_pt,
textcoords='axes fraction', va="center", ha="center", bbox=node_type,
arrowprops=arrow_args, FontProperties=font)
# 标注划分属性
def plot_mid_text(cntr_pt, parent_pt, txt_str):
font = FontProperties(fname=r"/System/Library/Fonts/STHeiti Medium.ttc", size=10)
x_mid = (parent_pt[0] - cntr_pt[0]) / 2.0 + cntr_pt[0]
y_mid = (parent_pt[1] - cntr_pt[1]) / 2.0 + cntr_pt[1]
create_plot.ax1.text(x_mid, y_mid, txt_str, va="center", ha="center", color='red', FontProperties=font)
# 绘制决策树,参考书籍《机器学习实战》绘图代码
def plot_tree(decision_tree, parent_pt, node_txt):
d_node = dict(boxstyle="sawtooth", fc="0.8")
leaf_node = dict(boxstyle="round4", fc='0.8')
num_leafs = get_num_leafs(decision_tree)
first_str = next(iter(decision_tree))
cntr_pt = (plot_tree.xoff + (1.0 + float(num_leafs)) / 2.0 / plot_tree.totalW, plot_tree.yoff)
plot_mid_text(cntr_pt, parent_pt, node_txt)
plot_node(first_str, cntr_pt, parent_pt, d_node)
second_dict = decision_tree[first_str]
plot_tree.yoff = plot_tree.yoff - 1.0 / plot_tree.totalD
for k in second_dict.keys():
if isinstance(second_dict[k], dict):
plot_tree(second_dict[k], cntr_pt, k)
else:
plot_tree.xoff = plot_tree.xoff + 1.0 / plot_tree.totalW
plot_node(second_dict[k], (plot_tree.xoff, plot_tree.yoff), cntr_pt, leaf_node)
plot_mid_text((plot_tree.xoff, plot_tree.yoff), cntr_pt, k)
plot_tree.yoff = plot_tree.yoff + 1.0 / plot_tree.totalD
def create_plot(dtree):
fig = plt.figure(1, facecolor='white')
fig.clf()
axprops = dict(xticks=[], yticks=[])
create_plot.ax1 = plt.subplot(111, frameon=False, **axprops)
plot_tree.totalW = float(get_num_leafs(dtree))
plot_tree.totalD = float(get_tree_depth(dtree))
plot_tree.xoff = -0.5 / plot_tree.totalW
plot_tree.yoff = 1.0
plot_tree(dtree, (0.5, 1.0), '')
plt.show()
if __name__ == '__main__':
watermelon_data = pd.read_csv('./watermelon.csv')
column_count = dict([(ds, list(pd.unique(watermelon_data[ds]))) for ds in watermelon_data.iloc[:, :-1].columns])
al_name = 'ID3'
d_tree = create_tree(watermelon_data, column_count,al_name)
print('ID3算法:',d_tree)
create_plot(d_tree)
al_name = 'C4.5'
d_tree = create_tree(watermelon_data, column_count, al_name)
print('C4.5算法:',d_tree)
create_plot(d_tree)
al_name = 'CART'
d_tree = create_tree(watermelon_data, column_count, al_name)
print('CART算法:',d_tree)
create_plot(d_tree)