博客

数组的每个下标作为一个阶梯，第 i 个阶梯对应着一个非负数的体力花费值 cost[i]（下标从 0 开始）。每当爬上一个阶梯都要花费对应的体力值，一旦支付了相应的体力值，就可以选择向上爬一个阶梯或者爬两个阶梯。请找出达到楼层顶部的最低花费。在开始时，你可以选择从下标为 0 或 1 的元素作为初始阶梯。

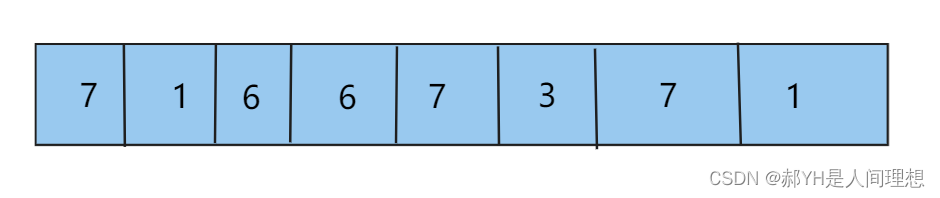
为了更好的帮助大家理解，如上图：

7 1 6 6 7 3 7 1

，如果想要爬到最顶层（也就是遍历到下标越界的地步）。应该选择下标为1/6/3/1的楼梯，也就是

1 6 3 1，

sum=11即为最小值。

本质思想：斐波那契数列。

斐波那契数列的思想是当前项是前两项的

和

，而对于本题，由于一次性可以跳1个或者2个，所以可以转化为：从前一个和前两个到当前位置，哪个所花费的体力值

小

一些。也就是说：


裴波那契是求前两项的sum，而本题是求前两项的min。


这是理解题目的关键。

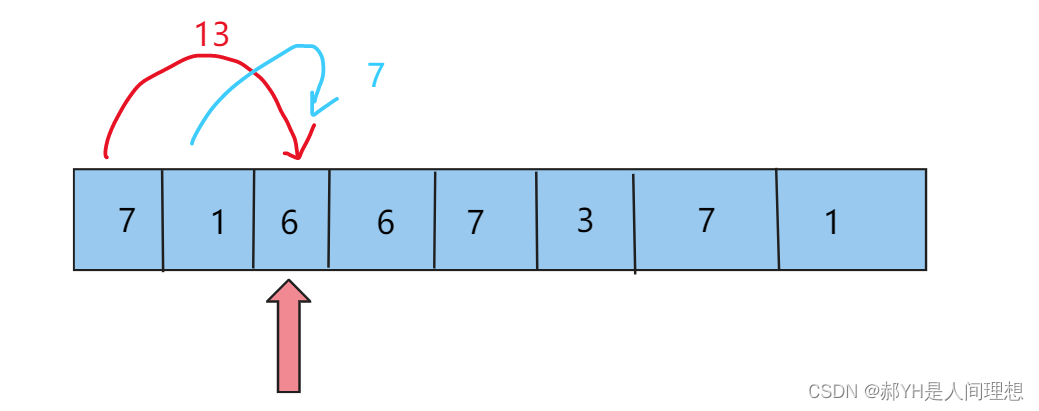
例如，想到达下标为2的6，要么从0开始，要么从1开始，相当于就是

选择出前两位哪一个到达当前位的代价最小——以此类推！

具体的代码实现如下：

#include <iostream>
#include <vector>
using namespace std;

/* run this program using the console pauser or add your own getch, system("pause") or input loop */

int main(int argc, char** argv) 
{
	int n=0;
	cin>>n;
	vector<int> G;
	//G数组用来存放题干中给出的代价 
	for(int i=1;i<=n;i++)
	{
		int temp=0;
		cin>>temp;
		G.push_back(temp);
	}
	
	vector<int> A;
	//A数组用于存放到达当前位置的最小代价！ 
	A.push_back(0);
	A.push_back(0);
	//制造两个初始阶梯，均为0 
	for(int i=2;i<=n;i++)
	{
		A[i]=min(A[i-1]+G[i-1],A[i-2]+G[i-2]);
		//核心：到达当前下标的最小代价，即为前一个的最小代价前另个的最小代价中的最小值。 
	}
	cout<<A[n]<<endl;
	
	return 0;
}

运行结果如下：与之前求出的11一致。

为了验证正确性，我们依次人为数出到达每一点的最小值：

仔细观察，每一项都是前两项的最小值加当前下标的代价。

遍历输出A数组，结果如下：

遍历出A与G的和，与上面的表格一致！（最后一位异常值越界，不用管）。