一、贪心算法的原理及其解析

1.什么是贪心算法？

贪心算法

（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，他所做出的是在某种意义上的局部最优解。 贪心选择是指所求问题的整体最优解可以通过一系列局部最优的选择，即贪心选择来达到。这是贪心算法可行的第一个基本要素。

2.怎么用贪心算法？

3.什么时候用贪心算法？

当发现一个问题的解决只需要考虑最优子结构的问题即可，即每一步最优，不需要考虑整体，而这时就可以用我们的贪心算法来解决问题。

二、贪心典型例题级解析

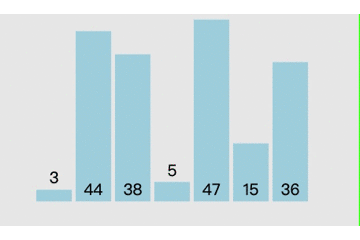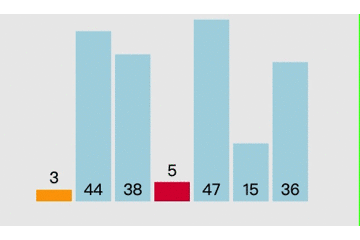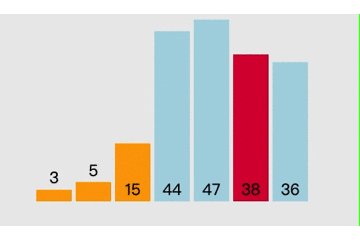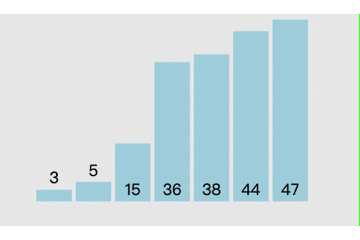
（一）选择排序

这里的贪心表现在于我每一步都选取当下最小的数来替换我，以实现排序，我不关心整体是一个声明样子，我只关心我这一步的最小值。

/*我们熟知的选择排序，其实采用的即为贪心策略。 
它所采用的贪心策略即为每次从未排序的数据中选取最小值，
并把最小值放在未排序数据的起始位置，直到未排序的数据为 0，则结束排序。 */
void swap(int* array, int i, int j) { 
int tmp = array[i]; array[i] = array[j]; array[j] = tmp; } 

void selectSort(int* arr, int n){ //i: 未排序数据的起始位置 
           for(int i = 0; i < n; ++i) { 
               int minIdx = i; //从所有未排序的数据中找最小值的索引 
               for(int j = i + 1; j < n; ++j){ 
                     if(arr[j] < arr[minIdx]) 
                                 minIdx = j; 
                     }
                       swap(arr, minIdx, i); 
           } 
}

（二）平衡字符串

力扣链接：

力扣

这里的贪心思想是什么呢？

说白了，因为只有R和L两个，只要R与L一样多时，就可以进行一分割，这时候，我们通过一个平衡点来记录此时的R与L个数的相差值，只要平衡点等于0就开始分割，这样就可以得到最大程度的分割平衡字符串

class Solution {
public:
    int balancedStringSplit(string s) {
     int balance =0;
     int count =0;
     for(int i =0;i<s.size();i++){
         if(s[i]=='R'){
             balance ++;
         }
         if(s[i]=='L'){
             balance--;
         }
         if(balance==0){
             count++;
         }
     }
      return count;
    }
};

（三）卖股票的最佳时机问题

力扣链接：

力扣

这里其实就是站在了上帝视角看问题，我怎么保证最大的利润，只有看第二天是增加还是减小，连续增加的情况下，我从最低点进行买入，到下一次即将要下跌的位置卖出，这个时候我的利润是最大的。

所以这里的贪心思想是什么呢？

我不关心整体是高是低，我只关心下一天如果比我今天高，我就买入，如果比我今天低，我就卖出。

代码实现：

class Solution {
public:
    int maxProfit(vector<int>& prices) {
        int temp =0;
    for(int i = 1;i<prices.size(); i++ ){
      if(prices[i]>prices[i-1]){
          temp +=prices[i]-prices[i-1];
      }
    }
    return temp;
    }
};

四、跳跃游戏

力扣链接：力扣

贪心思想：

在这里我们一个一个遍历， 在确保能到达的位置上。不断更新当前位置地最远能够到达地距离，如果遍历后最远到达地距离大于等于整个数组地长度，那么就一定可以走完。

class Solution { 
public: 
         bool canJump(vector<int>& nums) { 
             int n = nums.size(); 
             int rightmost = 0; 
             for (int i = 0; i < n; ++i) { //如果可以到达当前位置，则更新最大 
                   if (i <= rightmost) { //每次更新最大的位置 
                        rightmost = max(rightmost, i + nums[i]); //如果可以到达最后一个位置，则直接返回      
                  if (rightmost >= n - 1) { return true; } 
                   } }return false; 
          } 
   };

（五）钱币找零

#include<iostream> 
#include<algorithm> 
using namespace std; 
int solve(int money,const vector<pair<int,int>>& moneyCount) { 
            int num = 0; //首先选择最大面值的纸币 
            for (int i = moneyCount.size() - 1; i >= 0; i--) { 
            //需要的当前面值与面值数量取最小 
            int c = min(money / moneyCount[i].first, moneyCount[i].second); 
           money = money - c * moneyCount[i].first; 
            num += c; 
              }
             if (money > 0) num = -1; 
    return num; 
}

这个地方要分两种情况谈论，第一种情况，就是机器数大于任务数，那么最长的时间就是最长的任务的时间，如果机器数小于任务数，那么这个时候我们就应该让耗时最长的先放入，然后把添加的新任务添加到最快完成的一个机器队伍，才能实现最大。所以贪心思想就出来了。

贪心策略：

bool cmp(const int &x, const int &y) { return x > y; }
int findMax(const vector<int>& machines) { 
int ret = machines[0]; 
for (const auto& cur : machines) { 
        if (ret < cur) ret = cur; }
            return ret; }
int greedStrategy(const vector<int>& works, vector<int>& machines) { // 按作业时间从大到小排序 
     sort(works.begin(), works.end(), cmp); 
     int workNum = works.size(); 
     int machineNum = machines.size();
// 作业数如果小于机器数，直接返回最大的作业时间 
       if (workNum <= machineNum) { 
       int minimalTime = works[0]; 
          return minimalTime; 
           }else {// 为每一个作业选择机器 
            for (int i = 0; i < workNum; i++) { // 选择最小的机器 
           int flag = 0; //首先假设用第一个机器处理 
         int tmp = machines[flag]; // 从剩余机器中选择作业时间最小的 
         for (int j = 1; j < machines.size(); j++) { 
                if (tmp > machines[j]) { flag = j; tmp = machines[j]; } }// 将当前作业交给最小的机器执行 
            machines[flag] += works[i]; }// 从所有机器中选出最后执行完作业的机器 
            int minimalTime = findMax(machines); 
             return minimalTime; } 
}

当


n<=m


时，只要将作业分给每一个机器即可；当


n>m


时，首先将


n


个作业从大到小排序，然后依此顺序将作业分配给空闲的处 理机。也就是说从剩下的作业中，选择需要处理时间最长的，然后依次选择处理时间次长的，直到所有的作业全部处理完 毕，或者机器不能再处理其他作业为止。如果我们每次是将需要处理时间最短的作业分配给空闲的机器，那么可能就会出现其它所有作业都处理完了只剩所需时间最长的作业在处理的情况，这样势必效率较低。

（七）队列活动

有


n


个需要在同一天使用同一个教室的活动


a1, a2, …, an


，教室同一时刻只能由一个活动使用。每个活动


a[i]


都有一个 开始时间s[i]


和结束时间


f[i]


。一旦被选择后，活动


a[i]


就占据半开时间区间


[s[i],f[i])


。如果


[s[i],f[i])


和


[s[j],f[j])


互不重 叠，a[i]


和


a[j]


两个活动就可以被安排在这一天。求使得尽量多的活动能不冲突的举行的最大数量。

#include<iostream> #include<algorithm> 
#include <vector> using namespace std; 
bool cmp(const pair<int,int>& a, const pair<int,int>& b) { 
return a.second < b.second; 
}
int greedyActivitySelector(const vector<pair<int,int>>& act) { 
//贪婪策略：每次选择最早结束的活动 
int num = 1, i = 0; for (int j = 1; j < act.size(); j++) {
//贪心策略 1. 每次都选择开始时间最早的活动，不能得到最优解。 
//2. 每次都选择持续时间最短的活动，不能得到最优解。
   if (act[j].first >= act[i].second) { 
         i = j; 
           num++; } 
}return num; 
}

三、贪心算法的总结

我们还要知道的是，贪心算法是一个适用度较小的算法，因为它存在一些缺陷，所以，我们在决定使用贪心算法的时候应该明确：

该算法存在的问题

不能保证求得的最后解是最佳的

不能用来求最大值或最小值的问题

只能求满足某些约束条件的可行解的范围