目录

问题描述
设有一个背包可以放入物品的重量为s,现有n件物品,重量分别为w[0], w[1], …,w[n – 1]。
能否从这n件物品中选择若干件放入此背包使得放入的重量之和正好等于s。
如果存在一种符合上述要求的选择,则称此背包问题有解:否则,称此背包问题无解。
问题示例
s = 10,n=6, 物品重量为{ 1,8,4,3,5,2 }时
可找到下列4组解:{ 1,4,3,2 },{ 1,4,5 },{ 8,2 },{ 3,5,2 }。
输入输出
用户输入重量s、n以及n件物品的重量
如果有解则输出所有的解。
如果无解,则输出背包问题无解。
递归定义
true表示有解,false表示无解
s=0 true 此时问题有解
s<0或者n<1 false 总重量和物品件数不能为负数
s>0且n>=1 KNAP(s,w,n-1) 所选物品不包括w[n-1]
s>0且n>=1 KNAP(s-w[n-1],n-1) 所选物品包括w[n-1]
递归函数
int pick[6] = { 0 };//记录要打印的物品的下标
int sz = 0;//记录打印答案的个数
int flag = 0; //标志符号:记录有没有解
int KNAP(int s, int w[], int n)
{
if (s == 0)
{
printf("{ ");
for (int i = 0; i < sz; i++)
{
printf("%d ", w[pick[i]]);
}
printf("},");
flag = 1;
return 1;
}
else if (s < 0 || n < 1)
return 0;
else
{
KNAP(s, w, n - 1);//所选物品不包括w[n-1]
pick[sz++] = n - 1;//记录要打印的物品的下标
KNAP(s - w[n - 1], w, n - 1);// 所选物品包括w[n-1]
sz--;
}
return flag;
}
用法示例:
#include<stdio.h>
int pick[6] = { 0 };//记录要打印的物品的下标
int sz = 0;//记录打印答案的个数
int flag = 0; //标志符号:记录有没有解
int KNAP(int s, int w[], int n)
{
if (s == 0)
{
printf("{ ");
for (int i = 0; i < sz; i++)
{
printf("%d ", w[pick[i]]);
}
printf("},");
flag = 1;
return 1;
}
else if (s < 0 || n < 1)
return 0;
else
{
KNAP(s, w, n - 1);//所选物品不包括w[n-1]
pick[sz++] = n - 1;
KNAP(s - w[n - 1], w, n - 1);// 所选物品包括w[n-1]
sz--;
}
return flag;
}
int main()
{
int s= 0;
int n = 0;
int w[100] = { 0 };
printf("请输入一个背包可以放入物品的重量:\n");
scanf_s("%d", &s);
printf("请输入物品的个数:\n");
scanf_s("%d", &n);
printf("请输入物品的重量:\n");
for (int i = 0; i < n; i++)
{
scanf_s("%d", &w[i]);
}
if (KNAP(s, w, n))
printf("有解\n");
else
printf("背包问题\n");
return 0;
}
结果展示
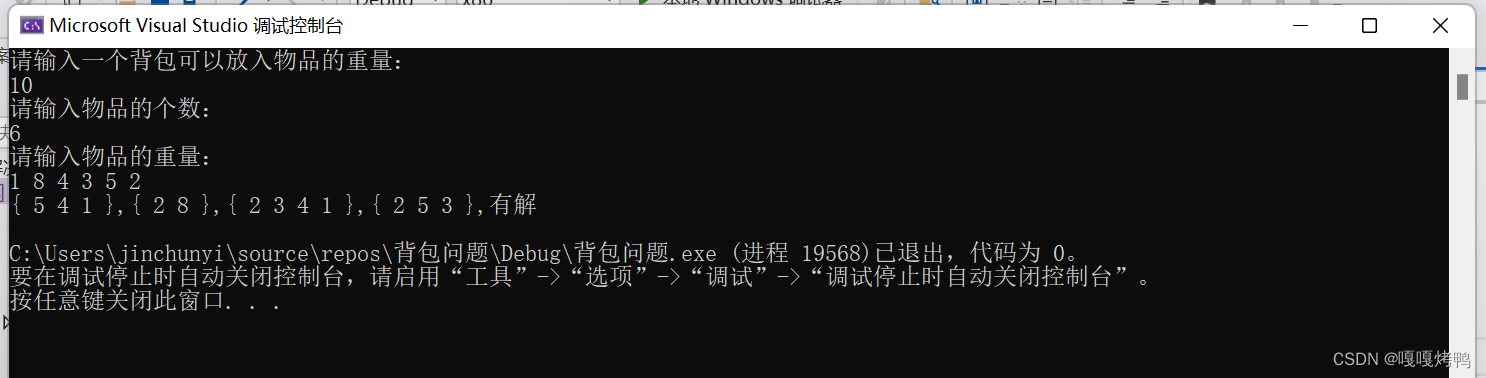

版权声明:本文为m0_65601072原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。