博客

递归

递归：就是自己调用自己，然后一层层返回

一个简单的例子：

打印问题：

	public static void main(String[] args) {
        test(4);
    }
    //打印问题
    public static void test(int n){
        if (n > 2){
            test(n-1);
        }
        System.out.println("n = "+ n);
    }

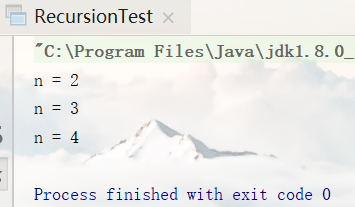
我们可以分析这个程序的执行过程：程序的方法在虚拟机的栈空间运行

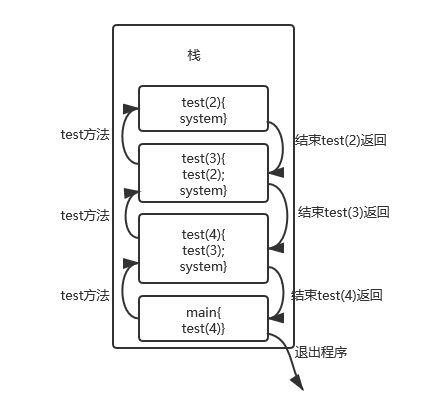
这就是递归的过程

递归的特点

• 递归方法都会创建独立空间（Java的JVM栈空间）
• 局部变量独立，引用变量、全局变量共享
• 函数定义中直接或间接地调用了本函数,必定存在可使递归调用终止的条件,否则导致出现无限递归
• 不能无限制地调用本身，须有个出口，且递归是向该出口逼近，化简为非递归状况处理
• 每次进入更深一层递归时，问题规模相比上一次递归都应有所减少，递归应当是简化问题
• 递归执行效率不高，递归层次过多会导致栈溢出

Java实现迷宫问题

有这样一个迷宫，从起点到终点，红色是墙，黄色的是路，可以走，一次走一格

如何实现？

1. 用数组模拟迷宫，0表示路，1表示墙

1 1 1 1 1 1 1 
1 0 0 0 0 0 1 
1 0 0 0 1 0 1 
1 1 1 0 1 0 1 
1 0 1 0 1 0 1 
1 0 1 1 1 0 1 
1 0 0 0 0 0 1 
1 1 1 1 1 1 1 

2. 约定：0 为该点没有走过 ；1 为墙；2为通路可以走；3表示该位置已经走过，但是走不通
3. 设置行走策略：迷宫时，策略为：下=》右=》上=》左，如果走不通再回溯，就是走到一个点，先看能不能向下，不能就看能不能向右等等，如果上下左右多不能，就回溯到上一个点

 /**
     * @param map 迷宫地图
     * @param i,j 开始位置(i,j)
     * @return 如果找到通路，就返回true，否则为false
     *
     * 使用递归回溯找到迷宫的路，设置终点为(6,5)
     * 约定：0 为该点没有走过 ；1 为墙；2为通路可以走；3表示该位置已经走过，但是走不通
     * 策略：走迷宫时，策略为：下=》右=》上=》左，如果走不通再回溯
     */
    public static boolean setWay(int[][] map ,int i,int j){

        //到达终点
        if (map[6][5] == 2){
            return true;
        }
        else {
            //当前这个点没有走过
            if (map[i][j] == 0){
                //按照策略走
                //假定该点可以走通
                map[i][j] = 2;
                //向下走
                if (setWay(map,i+1,j)){
                    return true;
                }
                //向右走
                else if (setWay(map,i,j+1)){
                    return true;
                }
                //向上走
                else if (setWay(map,i-1,j)){
                    return true;
                }
                //向左走
                else if (setWay(map,i,j-1)){
                    return true;
                }
                else {
                    //说明该点走不通，是死路
                    map[i][j] = 3;
                    return false;
                }
            }else {
                //如果map[i][j] !=  0，可能是1,2,3
                return false;
            }
        }
    }

测试：

	 public static void main(String[] args) {
        //二维数组模拟迷宫
        int[][] map = new int[8][7];
        //使用1表示墙
        //设置迷宫上下全为1
        for (int i = 0;i < 7;i++){
            map[0][i] = 1;
            map[7][i] = 1;
        }
        //左右为1
        for (int i = 1;i < 7;i++){
            map[i][0] = 1;
            map[i][6] = 1;
        }
        //设置挡板
        map[3][1] = 1;
        map[3][2] = 1;

        map[2][4] = 1;
        map[3][4] = 1;
        map[4][4] = 1;
        map[4][2] = 1;
        map[5][4] = 1;
        map[5][3] = 1;
        map[5][2] = 1;


        for (int i = 0;i < 8;i++){
            for (int j = 0;j < 7;j++){
                System.out.print(map[i][j]+" ");
            }
            System.out.println();
        }

        setWay(map,1,1);

        System.out.println("===完成后的迷宫===");

        for (int i = 0;i < 8;i++){
            for (int j = 0;j < 7;j++){
                System.out.print(map[i][j]+" ");
            }
            System.out.println();
        }
    }

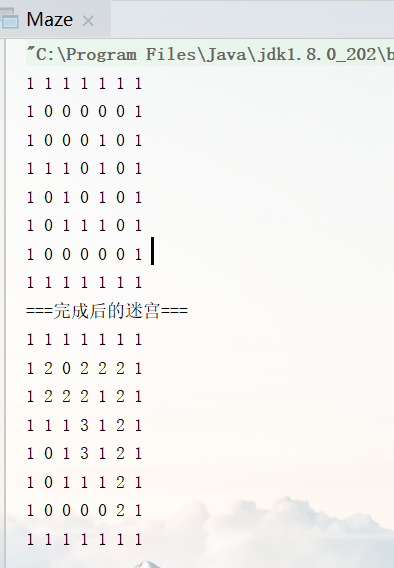
从结果看到，迷宫程序走的路线是：

一路按照策略走

• (1,1)下点为0，走到(2,1)
• (2,1)下点为1，右点为0，走到(2,2)
• (2,2)下点为1，右点为0，走到(2,3)
• (2,3)下点为0，走到(3,3)
• (3,3)下点为0，走到(4,3)
• 到（4,3）点，发现上下左右都不是0，设置(4,3)=3,回溯到（3,3）
• (3,3)发现上下左右都不是0，设置(3,3)=3,回溯到(2,3)
• (2,3)下点为3，右点为1，上点为0，走到(1,3)
• 继续按照策略，直到到达终点(6,5)

修改策略

我们上面的策略是下右上左，当然还有其他策略

如上右下左等等，实现方法就是将上面的ifelse语句顺序调换即可

	/**
     * @param map
     * @param i
     * @param j
     * @return
     *
     * 修改策略的找路径：上=》右=》下=》左
     */
    public static boolean setWay2(int[][] map ,int i,int j){

        //到达终点
        if (map[6][5] == 2){
            return true;
        }
        else {
            //当前这个点没有走过
            if (map[i][j] == 0){
                //按照策略走
                //假定该点可以走通
                map[i][j] = 2;

                //向上走
                if (setWay2(map,i-1,j)){
                    return true;
                }
                //向右走
                else if (setWay2(map,i,j+1)){
                    return true;
                }
                //向下走
                else if (setWay2(map,i+1,j)){
                    return true;
                }
                //向左走
                else if (setWay2(map,i,j-1)){
                    return true;
                }
                else {
                    //说明该点走不通，是死路
                    map[i][j] = 3;
                    return false;
                }
            }else {
                //如果map[i][j] !=  0，可能是1,2,3
                return false;
            }
        }
    }

这样再测试就可以看到：

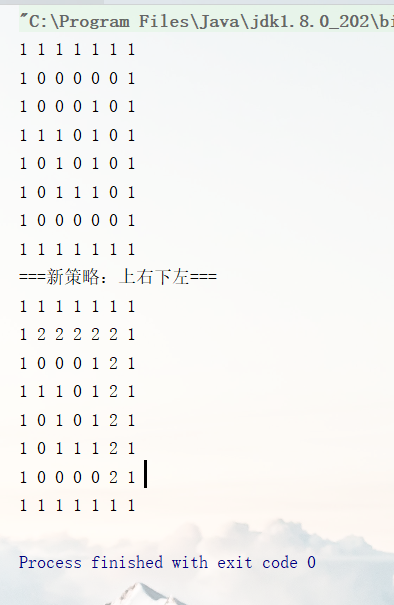
策略看自己的使用

总结

一个很复杂的迷宫问题，通过递归很简单就解决了

递归是一个很重要、很有用的思想，很多问题都可以通过递归解决

下一篇，递归实现八皇后问题