1 为什么要做A/B实验?
A/B实验,是一种验证假设的方法,其核心方法及原理分别是
对照实验
及
假设检验
。
在实际实验时会从总体抽取部分个体组成样本单位,并从个体实验结果推断总体结果。
1-1、实验原因
由于对照实验
遵循单一变量原则
,能通过对比发现因果性,并根据实验结果量化正向和负向的影响程度。
当实现了某个新的特性,我们无法准确预估上线后是增益还是减益,
从风险和成本的角度考量
,会切分小流量进行验证。
小型实验也意味着大部分能在单研发团队自助完成,时间和效率也能得到保障。
1-2、适用场景

A/B实验,解决的是策略优化问题,它能帮助我们从可选策略中选择最优策略。
它可以让我们在已达到的山上越来越高,却不能用它来发现一座新的山脉。
2 明确目的

数据分析的过程中一般的次序为:
相关性>>因果性>>效果
。
先通过数据分析洞察相关性,再通过实验提出假设,模糊预估其因果性。在证明成功后根据首次实验效果,持续优化时再进行清晰预估。
3 确认指标
1)正负指标

正向指标,一般依据实验路径制定,是策略好坏的直接评价,如:留存人数->点击人数->浏览人数->成交人数。
负向指标,适用于结果指标相近的场景
,如实验策略是下发公众号模板,其中两组的成交人数相近,但实验组却致使用户取关人数激增。
如正向收益小于负向收益,则应分析问题考虑优化实验或停止实验。
2)结果、过程、观察指标

结果指标是实验目的,过程指标体现如何完成。观察指标则指的相关性指标,多用于预估上升空间,如成交人数上升,但件均金额较低或购买对象仅覆盖本人。
依据观察指标,可以预估上升空间,并设计下一个实验。这3个指标在此前《数据分析的逻辑思维及分析方法》已有较全面的描述,在这里也不再赘述了,有兴趣的朋友可以查阅该文章。
4 制定策略
4-1、实验类型
1)互斥实验

遵循单一变量原则的代表是互斥实验,即用户同时间仅可进行一个实验,通过流量的互斥保障实验结果不受干扰。
但当实验越来越多,同时间可进行实验的用户量减少。流量不足,样本的代表性差。如果要等待前述实验结束再进行下一实验,验证周期增长、效率降低。
2)正交实验

为了解决互斥实验的流量问题,使用的方法是正交实验,也称分层实验。在此,分层的依据是不同的实验。
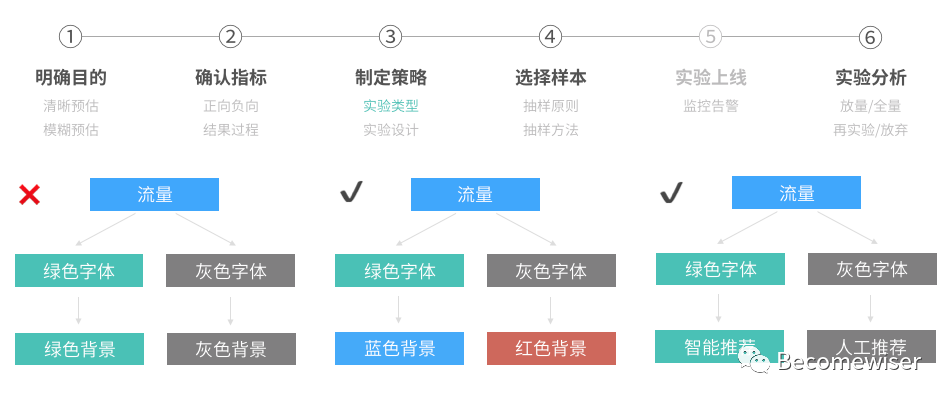
正交实验能使流量共享,同时进行多个实验,但我们需保障各层的划分参数相互独立且互不影响。
如:上一层的绿色字体不能与绿色背景正交。但绿色字体可以与蓝色背景正交实验,绿色字体也可以与只能推荐正交。
最后还有一个小的细节是,实验流量的来源不仅是上一层实验。这里涉及的内容可以参考谷歌的论文《Overlapping Experiment Infrastructure》。
4-2、实验设计
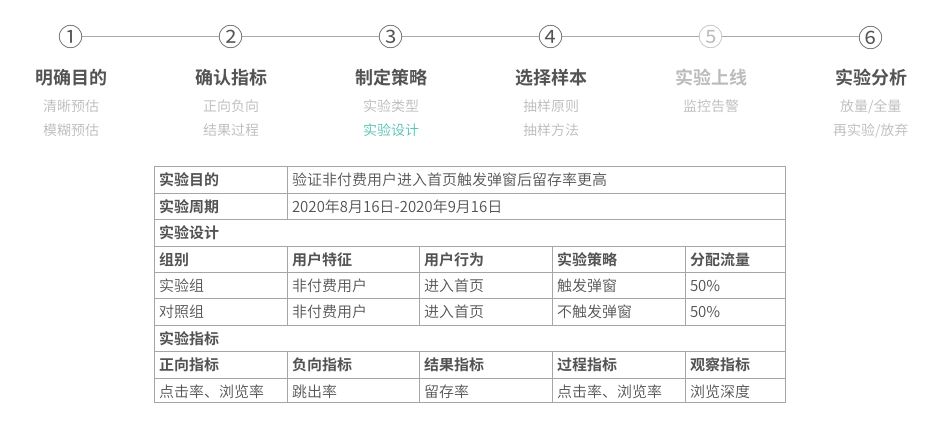
实验设计须注意的点是,尽量先粗后细,尽量先追求深度再追求广度。当产品有明显不佳的体验,其实更应该迅速迭代优化,并不是每件事都要有数据、有实验证明。
5 选择样本
5-1、抽样的原则

1)唯一性原则
唯一性指在用户进行实验时,从始至终仅命中相同的策略。帮助我们更准确的归因并让用户维持相同的体验。
2)均匀性原则
均匀性原则有两层定义,
数量的均匀
和
特征的均匀
。
前者是为了保证组间样本数量,
减少因数量小导致实验波动过大,后者则能使样本代表性更强
。假设分组中的女性占比过高,则实验的结论无法推断男性在这一实验中是否有类似的行为。
特征的均匀也应与实验目的相结合,如实验指标为某按钮点击率,实验组样本的点击率已在较高的基准线上,则可能无法分析策略优劣。
5-2、抽样方法

1)完全随机分组
完全随机分组,也称CR(Complete Randomization),是最常见的随机分组方式之一。常见的实现形式为对某ID字段哈希后对10取模,根据结果值进入不同的组。
如果随机选取ID进行哈希取模,那么是简单随机抽样。如果先将ID排序,逢6取1(6、16、26…)后再进行哈希取模,我们也称之为等距抽样。
2)重新随机分组
完全随机分组,由于不考虑样本的特征是否均匀,可能会导致某组样本的结果指标偏高或者偏低。为了解决此问题,我们可以AA实验观察样本差异或使用重新随机分组(ReRandomization)。
其原理为,每次随机分组后,通过验证组间差异是否小于设定的阈值。如果差异大于阈值,则重新分组,否则则停止分组。
此方法相比完全随机分组更准确,由于缺乏重跑的依据,得到合适的样本是概率性的,也可能造成很大的耗时。一般而言样本量越大,重分的次数越少。
3)自适应分组
Adaptive自适应分组,是滴滴AI Lab团队自研的分组方法,其能够在只分组一次的情况下,让选定的观测指标在分组后每组分布基本一致。
它在每次分组的时,记录当前分配的样本数以及样本分布,并计算当前对象分配至该组后该组的特征均匀情况,从而决定应分至哪个组。
6 实验分析
6-1、放量/全量

A/B实验,是小流量验证的实验方式,那我们应如何放量呢?
其前提如下:
1)结果显著,至少保证95%的可信度。
2)正向指标价值>负向指标价值
3)效果稳定,不因时间周期等元素变化剧烈波动
常见的放量方式有两种,
流量开放以及实验推广
。流量开放包含了实验内对照组和实验组流量的切分,也可在源头再增加样本。
实验推广,则是将此实验在其他特征、行为的群体中推广
。
6-2、再实验&终止
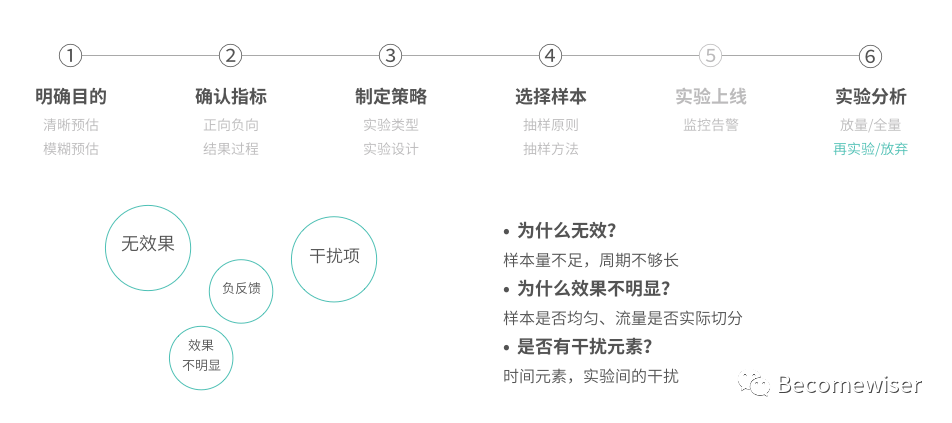
再实验的原因,从效果的次序来看是:
无法肯定是否有效果->无效果->效果不明显->负反馈。
负反馈如果影响了核心流程,则应考虑终止实验。
关于这2者的分析方法和需求分析是相近的,可以参考逻辑树“自下而上”的方法,先将每1环节可能出现的问题,再依次向上聚合。
7 几个理论
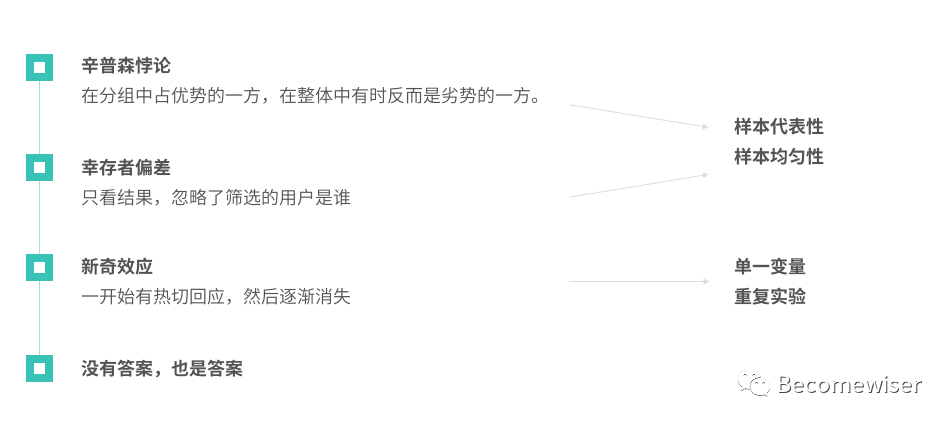
1)辛普森悖论
在分组中占优势的一方,在整体中有时反而是劣势的一方。
2)幸存者偏差
只看结果,却忽略了呈现结果的用户是谁。
3)新奇效应
一开始对实验策略有较好的回应,但一段时间迅速消失。
前2者,主要用于探究样本的代表性和均匀性。新奇效应则应在单一变量下,重复、长时地进行实验,保障实验结果不受实验影响。
写在最后
这篇文章始终感觉难度很大,从双盲实验到A/B实验,这两个词已经被成千上万的文章解读过很多遍,让我甚至写不出前言。最终选择的切入点是,逻辑梳理和知识再提炼。
也因为再提炼,会根据自身的理解省略了前期建设、上线监控等环节,其中监控更适合开单章,而数学、算法原理已经有朋友总结了很全面了,有兴趣的朋友可以阅读下方的参考资料。
感谢你看到这里,谢谢。
参考资料
1、腾讯PCG-E计划:实验设计及决策基础篇
2、ABtest 和假设检验、流量分配
https://www.6aiq.com/article/1555861276270?p=1&m=0
3、假设检验的运用
https://www.cnblogs.com/wobujiaonaoxin/articles/11910326.html
4、abtest-数据分析-假设检验基础
https://cloud.tencent.com/developer/article/1427845
5、哈希表是什么
http://www.woshipm.com/pmd/805326.html
6、区块链节点间的数据验证:哈希值与非对称加密
http://www.woshipm.com/blockchain/1019704.html
7、Overlapping Experiment Infrastructure重叠的实验基础设施
https://max.book118.com/html/2018/0131/151334020.shtm
8、AB实验在滴滴数据驱动中的应用