博客

在您阅读本文之前：

开发环境参照

https://blog.csdn.net/zhangchao19890805/article/details/78781003

正文开始。

学习 TensorFlow 让我的思维发生了变化。

计算机本质上是一种数学的工具，而我在学习编程的时候，思维也不可避免地收到了影响。传统的编程思想，常常认为程序就应该像数学定理或者数学函数一样，给出一个确定的结果。这是一种基于逻辑推导的思维习惯。

然而，做实验的科学家们的思维却不像数学家一样。实验科学家通过做实验收集数据，再根据数据推测其中蕴含的某种规律。

这篇文章以胡克定律为例子，向新手介绍如何使用TF。胡克定律是由物理学家胡克发现。简单地说，这个定律指弹簧长度的增量和弹簧受力大小呈正比关系。（注：这并不是胡克定律的严格定义，只是为了方便读者理解而作的简化说明。这个说法更像中学物理对胡克定律的说明。）

现在假设你是一个实验物理学家，要探索弹簧长度增量和受力大小之间的关系。你对一个弹簧施加了不同的力，并记录下了弹簧的增量（数据都是我瞎编的），存储到一个CSV文件中。文件名是 HookeLaw.csv

HookeLaw.csv文件内容

"force","length_variation"
8.0,3.9
4.3,2.2
5.7,3
7.2,4.1
10,5.2
21,9.0
14.5,7.1
11.3,5.8
12.3,6.1
21.3,10.5
18.2,9.8
21.3,10.8
21.5,10
19.1,9.8
32.3,15.9
28.3,14.0
33.3,16.2
30.3,15.5
31.7,17.1
29.9,14.6
30.5,14.9
34.5,17
9.9,10
35.5,18
29.9,15.0

这个样是看不出什么有价值的信息。你需要画出一个图表来进行判断。如果是在胡克那个时代，只能用手画出图表。现在只需用Python就可以了。我把 HookeLaw.csv 文件放到了 nginx 服务器上，方便 Python 读取。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# 从CSV文件中读取数据，并返回2个数组。分别是自变量x和因变量y。方便TF计算模型。
def zc_read_csv():
    zc_dataframe = pd.read_csv("http://yoursize.com/HookeLaw.csv", sep=",")
    x = []
    y = []
    for zc_index in zc_dataframe.index:
        zc_row = zc_dataframe.loc[zc_index]
        x.append(zc_row["force"])
        y.append(zc_row["length_variation"])
    return (x,y)

x, y = zc_read_csv()

# 获得画图对象。
fig = plt.figure()
fig.set_size_inches(10, 4)   # 整个绘图区域的宽度10和高度4
ax = fig.add_subplot(1, 2, 1)  # 整个绘图区分成一行两列，当前图是第一个。
# 画出原始数据的散点图。
ax.set_title("Hooke's Law")
ax.set_xlabel("force")
ax.set_ylabel("length_variation")
ax.scatter(x, y)
plt.show()

程序运行结果：

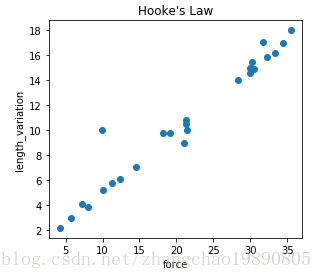
排除掉明显的误差数据，散点图看上去是一条直线。设弹簧长度增量是 y，受力是x，有理由推测 y = kx + b。在没有计算机的时代，需要手动画一条直线，并保持直线和各个点之间的距离最小，最后计算直线的 k 和 b。

因为有了计算机，我们可以用计算机来完成这些繁琐的工作。利用线性回归，让程序一点一点找到合适的b值和k值。在机器学习里面b和k叫做权重，用 w

₀

和 w

₁

表示。公式可以写成 y = w

₀

+ w

₁

x 。

下面的程序中，zc_x4tf 相当于是一个矩阵，在TF会话中是input：

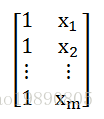
zc_y4tf 相当于是一个列向量，在TF会话中是weights：

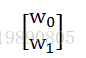
yhat = tf.matmul(input, weights) 可以理解成矩阵乘法，结果是预测值。

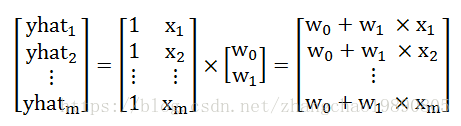
L2损失用于衡量每个实际值和预测值之间的偏差。对应概率论中的方差。

下面的程序给出了一个完整的实现。

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

# 从CSV文件中读取数据，并返回2个数组。分别是自变量x和因变量y。方便TF计算模型。
def zc_read_csv():
    zc_dataframe = pd.read_csv("http://yoursize.com/HookeLaw.csv", sep=",")
    x = []
    y = []
    for zc_index in zc_dataframe.index:
        zc_row = zc_dataframe.loc[zc_index]
        x.append(zc_row["force"])
        y.append(zc_row["length_variation"])
    return (x,y)

x, y = zc_read_csv()

zc_x = []
for item in x:
    zc_x.append([1., item])
zc_x4tf = np.array(zc_x).astype(np.float32)

zc_y = []
for item in y:
    zc_y.append([item])
zc_y4tf = np.array(zc_y).astype(np.float32)

# 存放 L2 损失的数组
loss_arr = []
# 训练的步数。即训练的迭代次数。
training_steps = 55
# 在梯度下降算法中，控制梯度步长的大小。
learning_rate = 0.01

# 开启TF会话，在TF 会话的上下文中进行 TF 的操作。
with tf.Session() as sess:
    # 设置 tf 张量（tensor）。注意：TF会话中的注释里面提到的常量和变量是针对TF设置而言，不是python语法。

    # 因为在TF运算过程中，x作为特征值，y作为标签
    # 是不会改变的，所以分别设置成input 和 target 两个常量。
    # 这是 x 取值的张量。设一共有m条数据，可以把input理解成是一个m行2列的矩阵。矩阵第一列都是1，第二列是x取值。
    input = tf.constant(zc_x4tf)
    # 设置 y 取值的张量。target可以被理解成是一个m行1列的矩阵。 有些文章称target为标签。
    target = tf.constant(zc_y4tf)

    # 设置权重变量。因为在每次训练中，都要改变权重，来寻找L2损失最小的权重，所以权重是变量。
    # 可以把权重理解成一个2行1列的矩阵。初始值是随机的。[2,1] 表示2行1列。
    weights = tf.Variable(tf.random_normal([2, 1], 0, 0.1))

    # 初始化上面所有的 TF 常量和变量。
    tf.global_variables_initializer().run()
    # input 作为特征值和权重做矩阵乘法。m行2列矩阵乘以2行1列矩阵，得到m行1列矩阵。
    # yhat是新矩阵，yhat中的每个数 yhat' = w0 * 1 + w1 * x。 
    # yhat是预测值，随着每次TF调整权重，yhat都会变化。
    yhat = tf.matmul(input, weights)
    # tf.subtract计算两个张量相减，当然两个张量必须形状一样。 即 yhat - target。
    yerror = tf.subtract(yhat, target)
    # 计算L2损失，也就是方差。
    loss = tf.nn.l2_loss(yerror)
    # 梯度下降算法。
    zc_optimizer = tf.train.GradientDescentOptimizer(learning_rate)
    # 注意：为了安全起见，我们还会通过 clip_gradients_by_norm 将梯度裁剪应用到我们的优化器。
    # 梯度裁剪可确保梯度大小在训练期间不会变得过大，梯度过大会导致梯度下降法失败。
    zc_optimizer = tf.contrib.estimator.clip_gradients_by_norm(zc_optimizer, 5.0)
    zc_optimizer = zc_optimizer.minimize(loss)
    for _ in range(training_steps):
        # 重复执行梯度下降算法，更新权重数值，找到最合适的权重数值。
        sess.run(zc_optimizer)
#         print(weights.eval())
        # 每次循环都记录下损失loss的值，病放到数组loss_arr中。
        loss_arr.append(loss.eval())
    zc_weight_arr = weights.eval()
    zc_yhat = yhat.eval()

print("weights", zc_weight_arr)


# 画出原始数据的散点图和数学模型的直线图。
def paint_module(fig):
    ax = fig.add_subplot(1, 2, 1)  # 整个绘图区分成一行两列，当前图是第一个。
    # 画出原始数据的散点图。
    ax.set_title("Hooke's Law")
    ax.set_xlabel("force")
    ax.set_ylabel("length_variation")
    ax.scatter(x, y)
    # 画出预测值的散点图。
    p_yhat = [a[0] for a in zc_yhat]
    ax.scatter(x, p_yhat, c="red", alpha=.6)
    # 画出线性回归计算出的直线模型。
    line_x_arr = [1, 40]
    line_y_arr = []
    for item in line_x_arr:
        line_y_arr.append(zc_weight_arr[0] + zc_weight_arr[1] * item)
    ax.plot(line_x_arr, line_y_arr, "g", alpha=0.6)

# 画出训练过程中的损失变化
def paint_loss(fig):
    print("loss", loss_arr)
    ax = fig.add_subplot(1, 2, 2)  # 整个绘图区分成一行两列，当前图是第二个。
    ax.plot(range(0, training_steps), loss_arr)


# 获得画图对象。
fig = plt.figure()
fig.set_size_inches(10, 4)   # 整个绘图区域的宽度10和高度4
paint_module(fig)
paint_loss(fig)

plt.show()

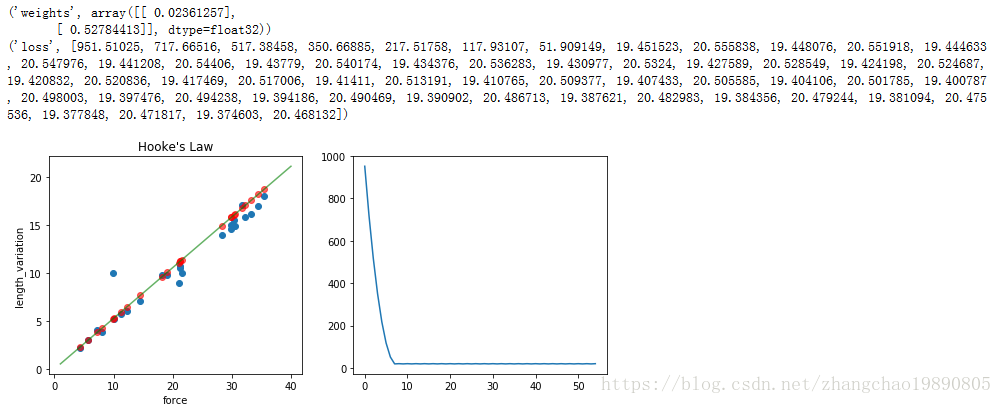
有结果可知 y = 0.5x + 0.2 变形得 x = 2y – 0.4

而胡克定律公式是 F = kL （F是力，k是弹性系数，L是弹簧长度增量）。可以把常数项 -0.4 看作系统误差，则弹簧弹性系数是2 。