本次实验的题目如下所示:
某一通信公司在一次施工中,需要在水面宽为 20m 的河沟底沿直线走向铺设一条沟底光缆。在铺设光缆之前需要对沟底的地形做初步探测,从而估计所需光缆的长度,为工程预算提供依据。大概情况如下图所示:
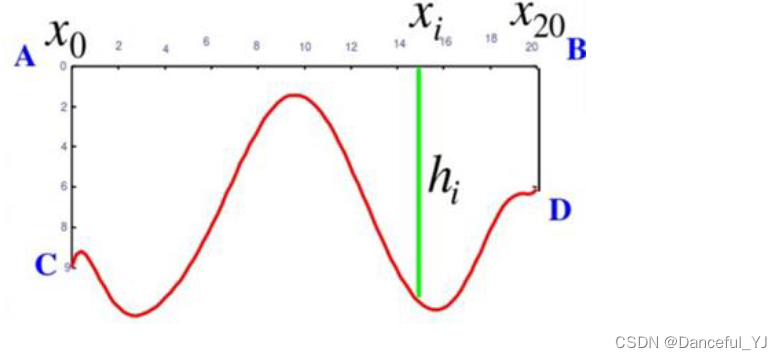
探测到一组等分点位置的深度数据如下表所示:

请你利用插值方法来解决以下的问题:
(1 )预测通过这条河沟所需光缆长度的近似值。
(2 )求出铺设沟底光缆的拟合曲线函数,并绘制其图像。
问题分析:
在第一问中,根据上述题意,我们需要利用插值法来解决这一问题,解决这一问题我们主要是需要用到比较准确的三样条插值法来求解,因为scipy库中有三样条插值法,所以我们就利用python来简单地完成这道题目,并且最终计算出其结果即可。
在第二问中,我们需要通过函数拟合的方式来进行分析,我们需要进行一个对比,总结三样条插值法和多项式拟合法在画图拟合效果方面的不同之处,这样有利于我们掌握插值法的优缺点,总体来说是比较简单的。
知识原理:
(1)三样条插值法实验原理
三次样条插值法是一种用于在一组给定数据点之间进行平滑插值的数值方法。它的计算原理如下
1.
给定一组数据点,我们希望找到一条曲线来穿过这些点,使得曲线在每个数据点处的值与给定数据点的值相匹配。
2.
三次样条插值法使用分段三次多项式来逼近曲线。每个数据段都使用一个三次多项式来描述。
3.
为了满足插值条件,三次样条插值法要求在每个数据段的两个相邻数据点之间,曲线的一阶导数和二阶导数连续。这些条件确保了曲线的平滑性和连续性。
4.
通过解一个线性方程组,可以确定每个数据段的三次多项式的系数,从而得到插值曲线。
总结起来,三次样条插值法使用分段三次多项式来逼近数据点之间的曲线,通过满足插值条件来保持曲线的平滑性和连续性。这种方法在许多应用中被广泛使用,如数据插值、曲线拟合等。
(2)多项式拟合法实验原理
多项式拟合是一种用于在给定数据点集合上拟合一个多项式函数的方法。它的原理如下:
1.
给定一组数据点,我们希望找到一个多项式函数来逼近这些点,使得多项式在每个数据点处的值与给定数据点的值相匹配。
多项式拟合使用一个多项式函数来表示拟合曲线。多项式函数由多个幂次项的系数组成。
2.
拟合的目标是找到最佳的多项式系数,使得拟合曲线与数据点的残差最小化。常见的方法是最小二乘法,通过最小化残差的平方和来确定最佳拟合。
3.
多项式的阶数决定了拟合的灵活性和复杂度。较低阶的多项式可能会产生较简单的拟合曲线,而较高阶的多项式可以更好地适应数据点,但也可能产生过拟合的问题。
4.
拟合过程通常使用数值优化算法来求解最佳的多项式系数。最常用的方法是最小二乘法,可以通过求解正规方程或使用迭代方法(如梯度下降法)来获得最佳系数。
总结起来,多项式拟合通过选择合适的多项式函数来逼近给定数据点,以最小化拟合曲线与数据点之间的残差。多项式拟合是一种简单而强大的拟合方法,常用于数据分析、曲线拟合和函数逼近等领域。
———————————-Question One Begin————————————–
(1)首先将实验的数据导入并且做成numpy矩阵:
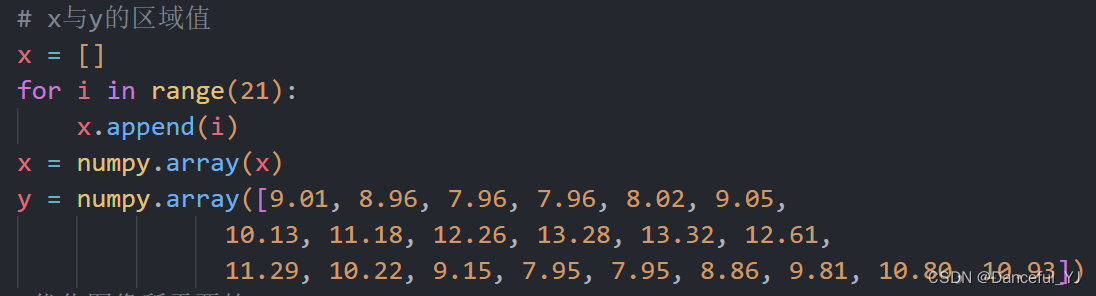
(2) 再引用Scipy中的库函数,将数据进行三样条插值计算并且求长度:

(3)其中微积分求弧长公式书写如下:
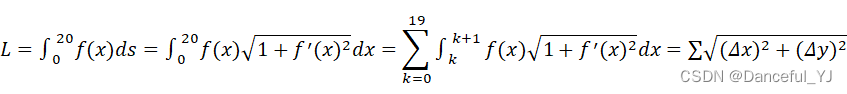
于是设计函数如下:

———————————-Question One End————————————–
———————————-Question Two Begin————————————–
根据上一题的结果,我们直接制作三样条插值法的可视化图像即可。
但是分析其绘图,我感觉过于理想化了,是不是太过于精确了呢?
于是我书写了多项式拟合的代码来进行两者的对比,代码如下:
Addition:多项式拟合法:

通过得出的图片进行两者的对比分析。
结果分析
:
(1)第一问答案:
三样条插值法得出:Length=26.6547(m)
![]()
多项式插值法得出:Length=25.9905
![]()
我们认为光缆长度应该在26.6547m左右
三样条插值法应该更为准确。
(2)第二问答案:
(1)三样条插值法拟合效果:
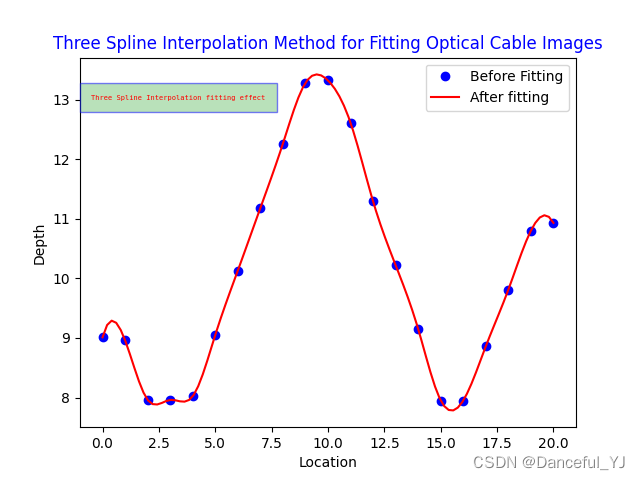
(
2
)多项式拟合法拟合效果
:
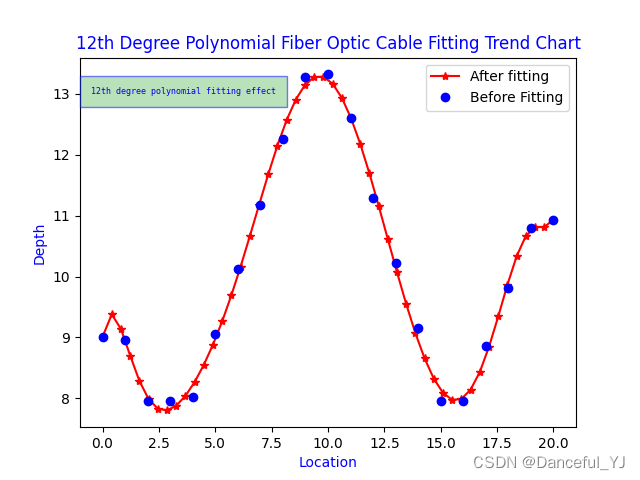
分析两张图片,我们发现三样条插值法的拟合效果非常好,几乎都覆盖了所有的点,而多项式插值法的效果图有几个点没有被拟合曲线连接。其实际上两种方法的差异在比较少的点的数量上差异不大,选取谁实际上还是需要根据实际的水下光缆情况来分析研究,不过个人感觉,多项式拟合法更像是拟合,存有些误差也是能够接受的,三样条插值法则显得比较完美了。
———————————-Question Two End————————————–
最后附上源代码
- 三样条插入法Python代码:
#库函数
import numpy
import matplotlib.pyplot as plt
from scipy import interpolate
from scipy.interpolate import interp1d
#函数声明区
# 微积分计算曲线积分的方法
def Computelength(x, y):
length = 0
for i in range(len(x) - 1):
dx = x[i + 1] - x[i]
dy = y[i + 1] - y[i]
length += numpy.sqrt(dx**2 + dy**2)
return length
# x与y的区域值
x = []
for i in range(21):
x.append(i)
x = numpy.array(x)
y = numpy.array([9.01, 8.96, 7.96, 7.96, 8.02, 9.05,
10.13, 11.18, 12.26, 13.28, 13.32, 12.61,
11.29, 10.22, 9.15, 7.95, 7.95, 8.86, 9.81, 10.80, 10.93])
#优化图像所需要的t
t=numpy.linspace(0,20,50)
#(1)第一题解答
# 通过scipy库计算三次样条插入法
spline = interpolate.splrep(x, y)
x_range = numpy.linspace(0, 20, 100)#开始计算光缆的长度
y_range = interpolate.splev(x_range, spline)
length = Computelength(x_range, y_range)
print("通过河沟所需光缆长度的近似值:", length)# 打印近似光缆长度
#(2)第二问解答
#(2)三样条插值法
x_three = numpy.linspace(0, 20, 100)
y_three = interpolate.splev(x_three, spline)
plt.plot(x, y, 'o',color='b' ,label='Before Fitting')
plt.plot(x_three, y_three,color='r' ,label='After fitting')
plt.xlabel('Location')
plt.ylabel('Depth')
plt.title('Three Spline Interpolation Method for Fitting Optical Cable
Images',color='b')
text = plt.text(x=-0.5, y=13, s='Three Spline Interpolation fitting effect', #文本内容
fontdict=dict(fontsize=5, color='r',family='monospace',),
bbox={'facecolor': '#74C476', 'edgecolor':'b','alpha': 0.5, 'pad': 8,}
)
plt.legend()
plt.show()
#(2)绘制拟合函数(多项式拟合方法)
#多次拟合寻找曲线重合度最好n次多项式的拟合结果
res=numpy.polyfit(x,y,12)#计算12次多项式拟合的结果
y_p=numpy.polyval(res,t)
#绘制图像
plt.figure()
plt.title('12th Degree Polynomial Fiber Optic Cable Fitting Trend
Chart',color='b')#title
plt.xlabel('Location',color='b')
plt.ylabel('Depth',color='b')
plt.plot(t,y_p,'r*-',color='r',label='After fitting')#标签
plt.plot(x,y,'o',color='b',label='Before Fitting')#标签
text = plt.text(x=-0.5, y=13, s='12th degree polynomial fitting effect', #文本内容
fontdict=dict(fontsize=6, color='r',family='monospace',),
bbox={'facecolor': '#74C476', 'edgecolor':'b','alpha': 0.5, 'pad': 8,}
)
text.set_color('b')
plt.legend()
plt.show()
2.多项式拟合法计算Length:
import matplotlib.pyplot as plt
#设置坐标轴
t=numpy.linspace(0,20,21)
x=numpy.linspace(0,20,100)
#输入数据并且拟合
poly=[9.01,8.96,7.96,7.96,8.02,9.05,10.13,11.18,
12.26,13.28,13.32,12.61,11.29,10.22,9.15,7.95,
7.95,8.86,9.81,10.80,10.93]
#多次拟合寻找曲线重合度最好n次多项式的拟合结果
res=numpy.polyfit(t,poly,12)#计算11次多项式拟合的结果
y_p=numpy.polyval(res,x)
#计算长度
Length=0
for i in range(2,100):
Length=Length+numpy.sqrt((x[i]-x[i-1])**2+(y_p[i]-y_p[i-1])**2)
print("通过河沟所需光缆长度的近似值:",Length)