博客

一、引言

二叉树在应用时，经常需要知道二叉树的深度。二叉树的深度就是二叉树的层数，即从树根算起，到最底下一层的层数是多少，即二叉树中结点的最大层次值。

本文给出了计算二叉树深度的算法，包括递归算法和非递归算法。

二、计算二叉树的基本方法

如下图所示的二叉树，其深度是4。



说到层数，大家自然会想到二叉树的层次遍历法。没错，其实我们只要一层一层的来遍历二叉树，当遍历到每一层的最右侧结点时，一层就遍历结束，因此可以考虑把每一层的最右侧结点作为每一层的标志，每当访问到该结类点时，二叉树的层数就可以增加1。

现在就会遇到一个问题：如何识别每一层最右侧的结点呢？

这时得回忆一下层次遍历算法，使用了队列来缓存二叉树上全部的结点，当初并没有识别每一层的最右侧结点。但是我们在层次遍历的过程中会发现，队列的队首总会走到每一层最右侧的结点位置，因此可以考虑通过判断队首的位置来识别最右侧结点，进而就可以得到层数。而且大家还会发现一个结论，那就是每一层最右侧的结点的左或者右子树也可能是下一层的最右侧结点（层尾结点）。当发现了这个结论，那么计算二叉树的深度就变得轻而易举了。

下面以上图为例演示一下按照层次遍历时，来识别二叉树深度的过程。

Step 1：树根a进队列，队列状态如下图所示：


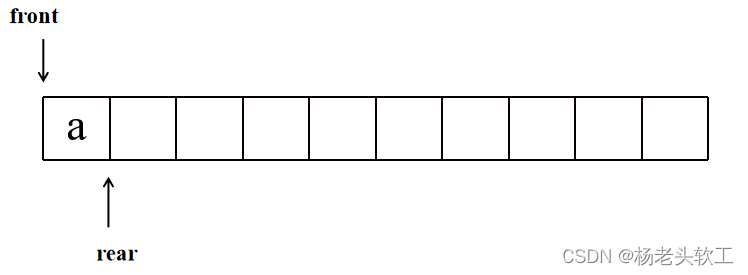
Step 2：队首出队列，队列状态如下图所示：



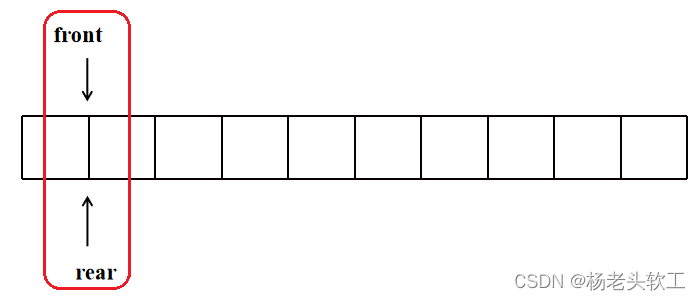
此时队首和队尾指向了同一个位置，也就是第一层遍历结束了，之后访问出队列的元素，并判断其左右子树是否为空，不空则继续入队列，所以就得到如下图所示的队列：

Step 3：结点a的左、右结点入队列



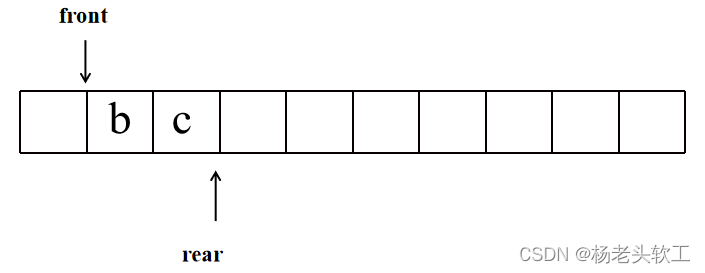
此时，其实我们又发现了：rear指向了队尾的前一个位置，就是一层结束的位置，如果在此处设个标志，是否可行？我们接着往下看。

Step 4：队首继续出队列、访问，访问之后，其左右子树非空的话，则继续入队列。


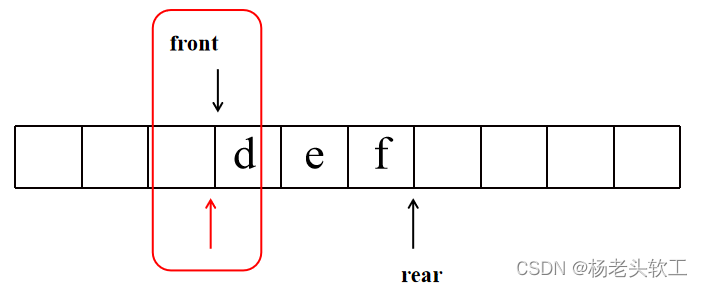
当连续两次队首出队列之后，队列状态如上图所示，这是就会发现front的位置和新增加的标志位置相同了，这是其实又是一层的结束位置。

到这里，是不是就可以发现，引入这个标志的用处了？

因为当前层最后一个结点，它的左子树或者右子树也基本上就是下一层的最后一个结点，当然了如果当前层的最右侧结点的左右子树同时为空，则也可能是再左侧一些的结点是下一层的队尾（如图中所示的结点g就不是上一层尾结点的子树）。因此，我们在设定了当前层最右侧标志之后，则该最右侧结点的左或右子树入队列后的队尾，是不是就可能是新的标志位了？对头，就是这样的。

所以当某个结点的左右子树入队列的时候，队尾就可能是一层的结束位置。这也就是为什么在算法中是执行了某个结点的左右子树都入队列之后才判断是否是一层的结束了。（说的好像有点啰嗦了，原谅我）

进而只需要判断队首front的值和新增加的标志（不妨记为levelLoc）的值是否相同即可，相同则表示一层结束，总层数就可以加1了，同时把levelLoc的值更新为队列当前的队尾这是因为此时队尾可能就是上一层队尾的子树。

后面的步骤就不用再赘述了，直接上代码。

三、计算二叉树深度的源代码：

1、结点结构

typedef struct node
{
	char data;
	struct node *Lchild;
	struct node *Rchild;
}BiTree;

2、递归算法

int BiTreeDepth( BiTree *T )
{
	int dep1 = 0, dep2 = 0;
	if ( T == NULL )
		return 0;
	else
	{     
		dep1 = BiTreeDepth( T->Lchild );
		dep2 = BiTreeDepth( T->Rchild ); 
		if ( dep1 > dep2 )  
			return dep1 + 1;
		else         
			return dep2 + 1;
	}
} 

3、非递归算法

int Search_Depth( BiTree *T)
{
	BiTree  *Queue[MAX_NODE]
    BiTree  *p = T;
	int  front=0 , rear=0, depth=0, levelLoc;
	// level总是指向访问层的最后一个结点在队列的位置
	if( T != NULL )
        Queue[++rear] = p;    //根结点入队
    levelLoc = rear;               //根是第1层的最后一个节点
    while ( front < rear )
	{
		p = Queue[ ++front ]; 
		if ( p->Lchild != NULL )   Queue[ ++rear ] = p->Lchild; //左结点入队
		if ( p->Rchild != NULL )   Queue[ ++rear ] = p->Rchild; //右结点入队
		if ( front == levelLoc ) //访问到当前层的最后一个结点 
		{
			depth++;  
			levelLoc = rear; 
		}
	}
	return depth;
}

4. 配合使用创建二叉树的算法（参见二叉树专栏里的算法https://mp.csdn.net/mp_blog/manage/column/columnManage/11925622）就可以完整的运行了，此处不再赘述。