文章目录
一、自编码是什么?
自编码网络是一种基于无监督学习方法的生成类模型。
自编码就是让输入数据自己给自己编码,简单来说就是让输出等于输入!
举例: 重铸: ( 器皿、旧的锅碗瓢盆等)。
具体过程是怎么做的?
原器具(数据) >输入铸造设备(模型)与打压成碎块(特征提取) >碎块越小,新器具造的越好,也就是特征维度越高,特征提取的越好>重塑器具(使用特征生成原数据)→新器具(输出)
二、自编码网络结构
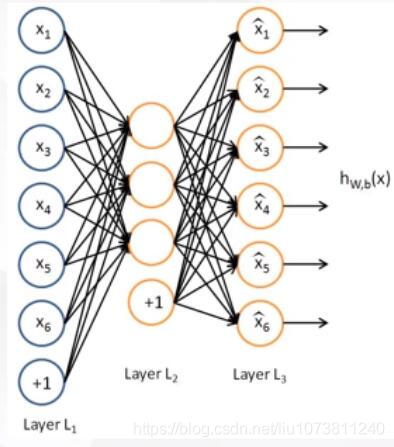
自编码网络的本质是图像的压缩再还原的过程,反映到图像上就是图像的编码部分和解码部分。
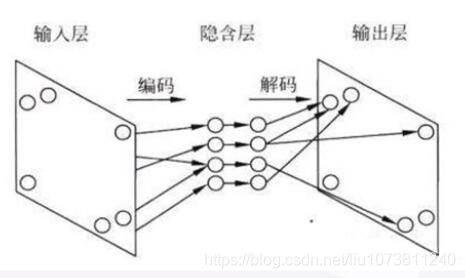
自编码网络的本质是图像的压缩再还原的过程,反映到图像上就是图像的编码部分和解码部分。
三:自编码网络运行过程
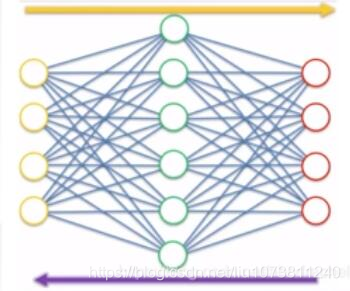
自编的过程就是网络先将输入的图像大小压缩到一定的范围(隐藏层),然后再还原到原来大小的过程,在这个过程中间,图像的大小是可以被还原的。
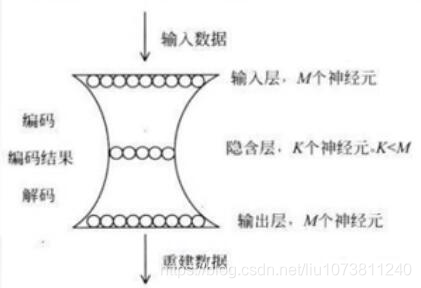
当然自编码隐藏层可以比输入层的神经元个数还多,然后我们可以在神经网络的损失函数构造上,加入正则化约束项进行稀疏约束,这个时候就演化成了稀疏自编码了。
如果不加正则化约束,会出现什么情况?模型学习不到任何东西。意味着输出数据不会发生任何噪声变化,完全和输入数据一样。一般做自编码是为了增加数据的多样性,比如增加样本。
四:使用自编码的原因
- 提取主要特征数据作为模型的输入,以减少计算量。
- 增加数据的多样性
五:自编码的特点
自编码是一种非监督学习,通常我们在使用自编码的时候通常只会使用自编码的前半部分,这个部分也叫作EnCode,编码器,编码器可以得到源数据的精髓(特征)。然后我们只需要在创建一个小的神经网络模型再去学习这个特征中的数据,不仅可以减少神经网络的负担,并且同样可以达到一个很好的效果。
压缩依靠的是输入数据(图像、文字、声音)本身存在不同程度的冗余信息,自动编码网络通过学习去掉这些冗余信息,把有用的特征输入到隐藏层中。这里和PCA有些类似,要找到可以代表源数据的主要成分。自编码器通过隐藏层对输入进行压缩,并在输出层中解压缩,整个过程肯定会丢失信息,但是通过训练我们能够使丢失的信息尽量减少,最大化的保留其主要精髓(特征)。
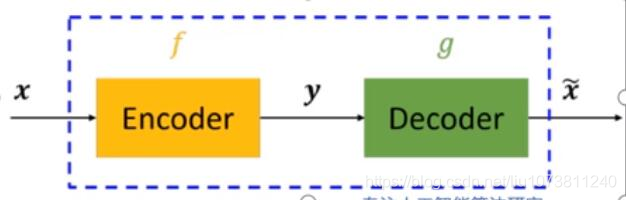
上图中,虚线蓝色框内就是一个自编码器 模型,它由编码器(Encoder)和解 码器(Decoder)两部分组成,本质上都是对输入信号做某种变换。编码器将输入信号x变换成编码信号y,而解码器将编码y转换成输出信号x‘。即y=f(x),x’ = g(y) = g(f(x))。
自编码器的目的是,让输出x尽可能复现输入x。如果f和g都是恒等映射(隐藏层特征大于输入层),那不就恒有x’=x?不错,但是这样的变换没啥作用。因此,我们对中间信号y做一定的约束,这样,系统往往能学出很有趣的编码变换f和编码y。
对于自编码器,我们需要强调一点是,我们往往并不关心输出是啥(反正只是复现输入),我们关心的是中间层的编码,或者说是从输入到编码的映射。可以这么理解,我们在强迫编码y和输入x不同的情况下,系统还能复原原始信号x,那么说明编码y已经承载了原始数据的所有信息,但以另一种形式表现。这就是特征提取,而且是主动学出来的。实际上,自动学习原始数据的特征表达也是神经网络和深度学习的核心目的之一。
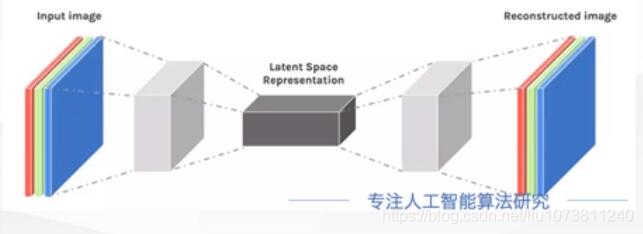
y= f(x) = s(wx+b)
x’ =g(y) = s(w’y+b’)
L(x,x’)= L(x,g(f(x))
其中L表示损失函数,结合数据的不同形式,可以是二次误差(squared error loss)或交叉熵误差(cross entropy loss)。为了尽量学到有意义的表达,我们会给隐层加入一定的约束。
从数据维度来看,常见以下两种情况:
1. n>p,即隐层维度小于输入数据维度。也就是说从x->y的变化是一种降维操作,网络试图以更小的维度去描述原始数据而尽量不损失数据信息。实际上,当每两层之间的变换均为线性,且监督训练的误差是二次型误差时,该网络等价于PCA。
2. n<p,即隐层维度大于输入数据维度(无意义)。这里有一 种情况,我们约束y的表达尽量稀疏(有大量维度为0,未被激活,增加正则化约束实现),此时的编码器便是“稀疏自编码器”。从特征的角度来看,稀疏的表达意味着系统在尝试特征选择,找出大量维度中真正重要的若干维。
六:自编码网络的种类
1. 普通自编码网络(Autoencoder)
普通自编码网络也叫欠完备的自编码器,从自编码器获得有用特征的一种方法是限制h的维度比x小,这种编码维度小于输入维度的自编码器称为欠完备(undercomplete) 自编码器。学习欠完备的表示将强制自编码器捕捉训练数据中最显著的特征。
当解码器是线性的且L是均方误差,欠完备的自编码器会学习出与PCA相同的生成子空间。这种情况下,自编码器在训练来执行复制任务的同时学到了训练数据的主元子空间。
因此,拥有非线性编码器函数f和非线性解码器函数g的自编码器能够学习出更强大的PCA非线性推广。不幸的是,如果编码器和解码器被赋予过大的容量,自编码器会执行复制任务而捕捉不到任何有关数据分布的有用信息。(容量要小)
附上实现普通自编码网络的代码:
(https://github.com/liu1073811240/Auto-encoder)
2. 稀疏自编码网络(Sparse Autoencoder)
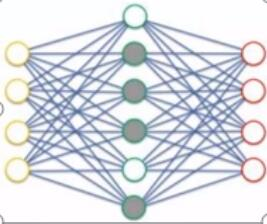
稀疏自编码器的隐藏层神经元大于输入层神经元,下图中隐藏中灰色的圆圈表示没有被激活的神经元。
之所以要将隐含层稀疏化,是由于,如果隐藏神经元的数量较大(可能比输入像素的个数还要多),不稀疏化我们无法得到输入的压缩表示。具体来说,如果我们给隐藏神经元加入稀疏性限制,那么自编码神经网络即使在隐藏神经元数量较多的情况下仍然可以发现输入数据中一些有趣的结构。
为了满足隐藏神经元的活跃度,将在优化目标中加入一个额外的惩罚因子,即正则项(L1、L2、dropout)。权重衰减和其他正则惩罚可以被解释为一个MAP近似贝叶斯推断,正则化的惩罚对应于模型参数的先验概率分布.
当神经元的输出接近于1时认为其被激活,输出接近0时则认为被抑制,那么使得神经元大部分时间都是被抑制的现在被称为稀疏性抑制。
3. 降噪自编码网络(Denoising Autoencoders)
人类具有认知被阻挡的破损图像能力,此源于我们高等的联想记忆感受机能。我们能以多种形式去记忆(比如图像、声音,甚至如上图的词根记忆法),所以即便是数据破损丢失,我们也能回想起来。

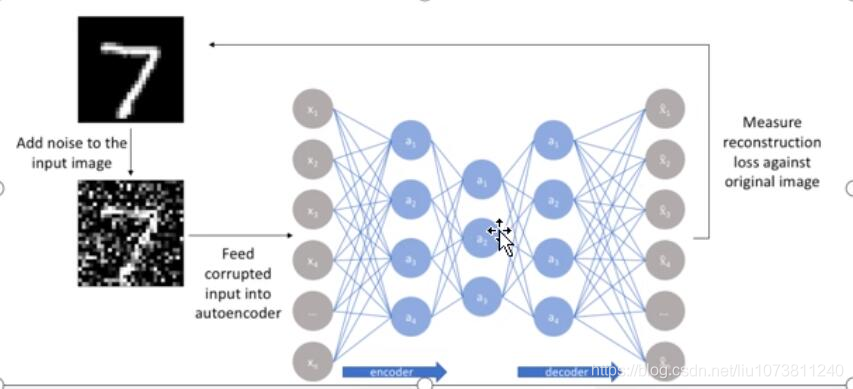
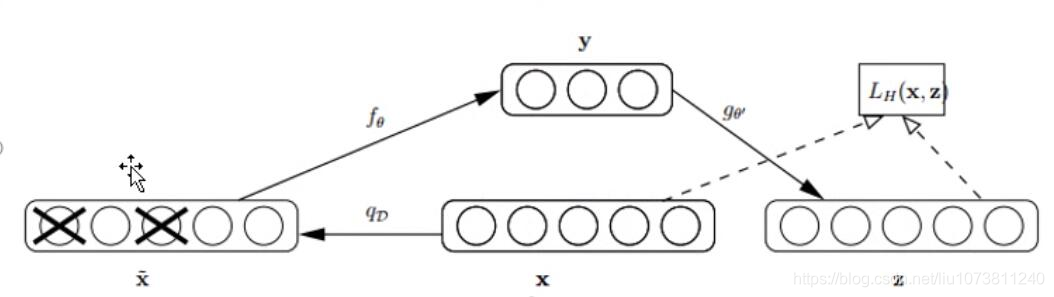
以一定概率分布(通常使用二项分布)去擦除(dropout) 原始input矩阵 ,即每个值都随机置o,这样看起来部分数据的部分特征是丢失了。以这丢失的数据x去计算y,计算z,并将z与原始x做误差迭代,这样,网络就学习了这个破损(原文叫Corruputed)的数据。
这个破损的数据是很有用的,原因有二:其之一,通过与非破损数据训练的对比,破损数据训练出来的Weight噪声比较小。降噪因此得名。原因不难理解,因为擦除的时候不小心把输入噪声给X掉了。
其二,破损数据一定程度上减轻了训练数据与测试数据的代沟。由于数据的部分被X掉了,因而这破损数据在一定程度上比较接近测试数据。( 训练、测试肯定有同有异,当然我们要求同舍异)。这样训练出来的Weight的鲁棒性就提高了。
4. 收缩自编码网络(Contractive Autoencoders)
降噪自编码网络利用重构函数抵抗输入的微扰;收缩自编码网络使用特征抽取函数来抵抗输入的微扰二者都是对输入的数据进行去噪,不同的是收缩自编码器的鲁棒性体现在对隐藏层表达上,而去噪自编码器的鲁棒性体现在重构信号中。
降噪自编码是普通的自编码,收缩自编码类似稀疏自编码(增加了正则项)。可以看作是降噪自编码+稀疏自编码。
5. 堆叠自编码网络(Stacked Autoencoders)
顾名思义,栈式自编码器就是多个自编码器级联,以完成逐层特征提取的任务,最终得到的特征更有代表性,并且维度很小。
栈式自编码器的训练过程是,n个AE按顺序训练,第1个AE模型训练完成后,将其编码器的输出特征作为第2个AE模型的输入数据,以此类推。最后得到的特征作为分类器的输入,完成最终的分类训练。
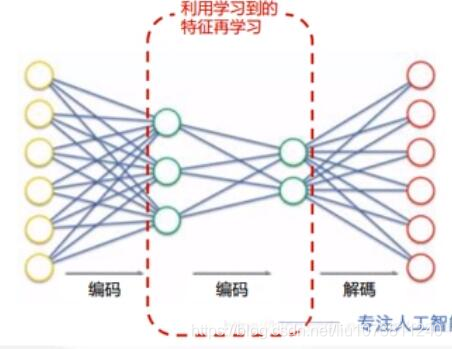
(多个编码器对应一个解码器的自编码模型)
6. 深度自编码网络(Deep Autoencoders)
使用预先训练好的层堆栈而成的限制玻尔兹曼机(Restriected Boltzemann machies)
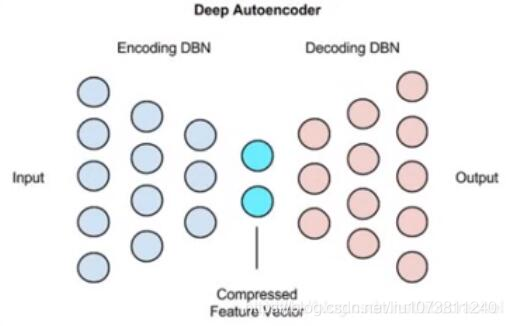
(训练好多个编码器对应多个解码器构成的一个深度自编码器)