博客

图论的基本概念

阶：节点集v中元素的个数

• n阶图 ； n个节点
• 空图：顶点集为空
• 零图：没有一条边的图
• 平凡图：即一阶零图
• 有限图：节点集合和边集合都是有限的

度

• 无向图

  • v节点作为边节点的次数成为度（环的节点的度为2）

• 有向图

  • 出度：v节点作为边起点的次数
  • 入度：v节点作为边终点的次数
  • 总度数：出度+入度

• 孤立点：度数为0的点

• 悬挂点：度数为1的点

• 偶点：度数为偶数

• 奇点：度数为奇数

定理

1. 总度数是边的两倍
2. 
   任何图中，度数为奇数的个数为偶数
   
3. 有向图中，出度之和等于入度之和等于边数

相邻

• 无向图：边的两个端点相邻，两条边至少有一个共同的端点，这两条边相邻
• 有向图：边的起点与终点相邻，若两条边的起点与终点重合，这两条边相邻

度数列

• 度数列：所有节点的度数的列表
• 入度列
• 出度列

定理

1. 度数列之和等于偶数（2倍边）
2. 入度列等于出度列之和
3. 可图化：怎么样的非负整数列可以作为度数列呢
   1. 奇数的个数为偶数（度定理2）
   2. 所有整数之和等于偶数（握手定理）
4. 可简单图化：略

简单图和多重图

1. 无向图

• 平行边：边关联同意对顶点
• 重数： 平行边的边数

2. 有向图

• 有向平行边：边的起点和终点相同
• 重数：同上

3. 简单图：没有多重边（平行边）也没有环
4. 多重图：有平行边

无向完全图和有向完全图

1. 无向完全图

• n阶无向简单图，若对于每个顶点都有n-1个顶点与其相邻，则称为n阶无向完全图，Kn
• 示例：
• 
• 
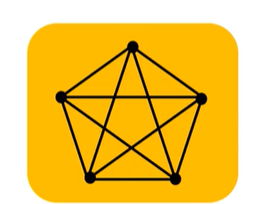
  边数：（n*（n-1））/2
  

2. 有向完全图

• n阶有向简单图，对于任意两点，都互作起点和终点，称为n阶有向完全图
• 示例：
  
• 
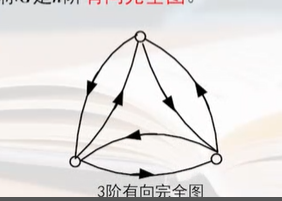
  边数：n*（n-1）
  

子图和真子图

1. 子图：
   
   
   
   
   每个图都是自身的子图
   

2. 生成子图：
   
   子集顶点集为母图的顶点集，称为子集为生成子集

3. G的v1导出子图G[v1]

• 点集为原图G的点集v的子集v1，且不为空

• 边集为G中两个端点都在v1中所组成的边

• 
  特殊的，G[v]=G
  

  G的E1导出子图G[E1]

• 边集为原图G的边集E的子集E1，且不为空

• 点集为与E1中边关联的点

• 
  特殊的，若G无孤立点，则G[E]=G
  

补图：

1. 无向简单图
   
   设
   
   
   
   G

   =

   V

   ,

   E

   G= V,E
   
   
   
   
   
   
   G
   
   
   
   
   =
   
   
   
   
   
   
   
   
   V
   
   
   ,
   
   
   
   
   E
   
   
   
   
   
   ,是一个n阶简单图，G的补图
   
   
   
   G

   ‾

   =

   V

   ‾

   ,

   E

   ‾

   \overline G= \overline V,\overline E
   
   
   
   
   
   
   
   
   
   
   
   
   
   G
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   =
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   V
   
   
   
   
   
   
   
   
   
   
   
   
   
   ,
   
   
   
   
   
   
   
   
   
   
   
   E
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   ,其中有
   
   
   
   
   
   E

   ‾

   =

   {

   (

   u

   ,

   v

   )

   ∣

   u

   ,

   v

   ∈

   V

   a

   n

   d

   (

   u

   ,

   v

   )

   ∉

   E

   }

   \overline E = \lbrace (u,v) | u,v \in V and (u,v)\notin E\rbrace
   
   
   
   
   
   
   
   
   
   
   
   
   
   E
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   =
   
   
   
   
   
   
   
   
   {
   
   
   
   (
   
   
   u
   
   
   ,
   
   
   
   
   v
   
   
   )
   
   
   ∣
   
   
   u
   
   
   ,
   
   
   
   
   v
   
   
   
   
   ∈
   
   
   
   
   
   
   
   
   V
   
   
   a
   
   
   n
   
   
   d
   
   
   (
   
   
   u
   
   
   ,
   
   
   
   
   v
   
   
   )
   
   
   
   
   
   
   ∈
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   /
   
   
   
   
   
   
   
   
   
   
   
   ​
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   
   E
   
   
   }
   
   
   
   
   
   

2. 有向简单图
   
   类似

3. 即图加上自身的补图应该变成一个完全图

同构

• 定义：即两个图，每个点都能找到对应的点，并且对应点关联形同的对应边，并且重数相等
• 必要条件：定点数相同，边数相同，度数序列相同（不计顺序），相邻的点相同

通路，回路和图的连通性

通路

• 定义：指从一个顶点到另一个顶点间的路
• 回路：当起点等于终点的时候，则称该路为回路

1. 简单通路（回路）
   
   通路（回路）中没有一样的边
2. 初级通路（回路）
   
   当除了v0,vn以外的所有的点都不同，所有的边都不同的通路，也称为路劲
   
   初级回路也类似，初级回路也称为圈
3. 复杂通路（回路）
   
   有重复边出现的通路（回路）

定理

• n阶图中，两点之间若存在通路，一定存在长度小于等于n-1的通路（或者初级通路）
• n阶图中，若一个点存在于到自身的回路，则一定存在小于等于n的到自身的回路（或者初级回路）（把所有的点都走一遍的回路，刚好为n）

连通

• 若两点之间有通路，则称这两点连通
• 有向图
  • 任意两点都是连通的，称为连通图，否则为非连通图
• 无向图
  • 弱连通图：略去有向图的边的方向后的无向图如果是连通图，则称该有向图为弱连通图，简称连通图
  • 单向连通图：有向图D中任意两定点至少一个可达另一个
  • 强连通图：D中任何一对顶点都是互相可达的

连通分支

• 无向图中根据顶点间的连通关系将无向图分为若干个连通分支，连通分支与连通分支之间没有连通
• 连通分支个数记为p（G）

删除

• 设v1是G顶点集V的子集，从G中删除v1的所有点，及v1所关联的边，称为删除v1
• 设E1是G边集的E的子集，从G中删除E1中的所有边，称为删除E1

点割集和边割集（割集）

• 点割集

用矩阵来表示图

关联矩阵

1. 无向图

• 元素aij表示i节点与j边的关联次数
• 0是不关联，1是关联一次，2是环
• 每个列相加等于2 每个边关联两个点
• 所有元素之和等于2倍边长
• 第i行表示i节点的度数

2. 有向图（不允许有环）

• 0表示不关联，1表示起点，-1表示终点
• 相加等于0，每个边有一个起点一个终点
• 每行1的数之和是出度，-1之和是入度的相反数

邻接矩阵

• 无向图

  • n阶无向图的邻接矩阵是n*n
  • 根据点与点之间的临界情况，1表示有邻接，0表示没有邻接
  • 环则该点与自己邻接
  • 无向图的邻接矩阵是对称的
  • 元素之和等于2倍边长（握手定律）

• 有向图

  • 不对称
  • 第i行是从i节点出发的边，第i列是到达i节点的边
  • 元素之和等于边数

邻接矩阵的性质（重点）

• 
• 推论
  • 设B= E+A^1 + A^2 …A^r,则B中的元素表示长度小于等于r的通路之和

可达矩阵或连通矩阵

1. 可达矩阵（有向图）

• 可达为1，不可达为0

• 对角线上都为1

• 
  
  计算方式
  

  • 将B（n-1）转化为布尔矩阵，非0的用1表示，0保持不变，就可以得到可达矩阵（n为节点数）

2. 连通矩阵（无向图）
   
   与可达矩阵相似