决策树(decision tree)(一)——构造决策树方法
说明:这篇博客是看周志华老师的《机器学习》(西瓜书)的笔记总结,虽然自己写了很多总结性文字包括一些算法细节,但博客中仍有部分文字摘自周老师的《机器学习》书,仅供学习交流使用。转载博客务必注明出处和作者,谢谢。
决策树系列博客:
决策树算法起源于E.B.Hunt等人于1966年发表的论文“experiments in Induction”,但真正让决策树成为机器学习主流算法的还是Quinlan(罗斯.昆兰)大神(2011年获得了数据挖掘领域最高奖KDD创新奖),昆兰在1979年提出了ID3算法,掀起了决策树研究的高潮。现在最常用的决策树算法是C4.5是昆兰在1993年提出的。(关于为什么叫C4.5,还有个轶事:因为昆兰提出ID3后,掀起了决策树研究的高潮,然后ID4,ID5等名字就被占用了,因此昆兰只好让讲自己对ID3的改进叫做C4.0,C4.5是C4.0的改进)。现在有了商业应用新版本是C5.0
link
。
一、决策树的基本概念
顾名思义,决策树就是一棵树,一颗决策树包含一个根节点、若干个内部结点和若干个叶结点;叶结点对应于决策结果,其他每个结点则对应于一个属性测试;每个结点包含的样本集合根据属性测试的结果被划分到子结点中;根结点包含样本全集,从根结点到每个叶子结点的路径对应了一个判定测试序列。下面直接上个图,让大家看下决策树是怎样决策的(以二元分类为例),图中红线表示给定一个样例(表中数据)决策树的决策过程:
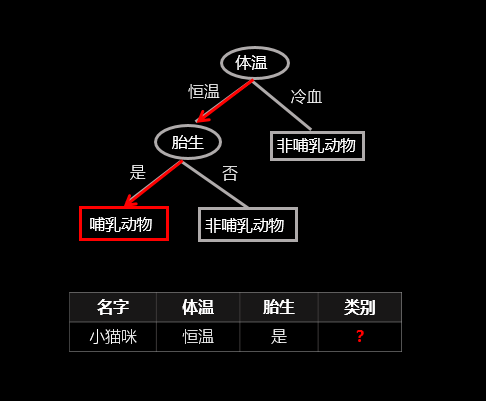
(
该图为原创
)
二、如何生成决策树
-
信息增益
决策树学习的关键在于如何选择最优的划分属性,所谓的最优划分属性,对于二元分类而言,就是尽量使划分的样本属于同一类别,即“纯度”最高的属性。那么如何来度量特征(features)的纯度,这时候就要用到“
信息熵
(information entropy)”。先来看看信息熵的定义:假如当前样本集D中第k类样本所占的比例为
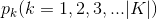
,
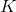
为类别的总数(对于二元分类来说,
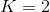
)。则样本集的信息熵为:
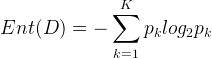
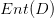
的值越小,则D的纯度越高。(
这个公式也决定了信息增益的一个缺点:即信息增益对可取值数目多的特征有偏好(即该属性能取得值越多,信息增益,越偏向这个),因为特征可取的值越多,会导致“纯度”越大,即ent(D)会很小,如果一个特征的离散个数与样本数相等,那么Ent(D)值会为0)。
再来看一个概念
信息增益(information gain),
假定离散属性

有

个可能的取值
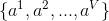
,如果使用特征

来对数据集D进行划分,则会产生V个分支结点, 其中第v(小v)个结点包含了数据集D中所有在特征

上取值为
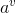
的样本总数,记为
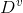
。因此可以根据上面信息熵的公式计算出信息熵,再考虑到不同的分支结点所包含的样本数量不同,给分支节点赋予权重
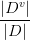
,即样本数越多的分支节点的影响越大,因此,
能够计算出特征

对样本集D进行划分所获得的“信息增益”:
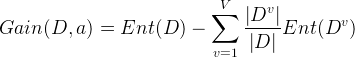
一般而言,
信息增益越大,则表示使用特征

对数据集划分所获得的“纯度提升”越大。所以信息增益可以用于决策树划分属性的选择,其实就是选择信息增益最大的属性,ID3算法就是采用的信息增益来划分属性。
下面来举个例子说明具体是怎样操作的,只贴公式没多大意义,还是有不利于大家理解。举例子用的数据集为:
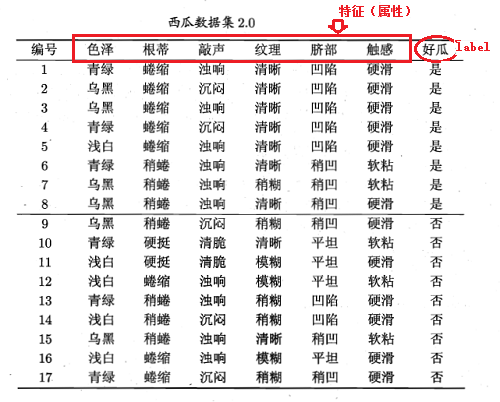
显然该数据集包含17个样本,类别为二元的,即
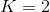
。则,正例(类别为1的样本)占的比例为:
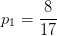
,反例(类别为0的样本)占的比例为:
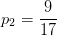
。根据信息熵的公式能够计算出数据集D的信息熵为:
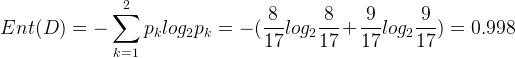
从数据集中能够看出特征集为:{色泽、根蒂、敲声、纹理、脐部、触感}。下面我们来计算每个特征的信息增益。先看“色泽”,它有三个可能的离值:{青绿、乌黑、浅白},若使用“色泽”对数据集D进行划分,则可得到3个子集,分别为:
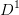
(色泽=青绿)、
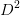
(色泽=乌黑)、
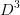
(色泽=浅白)。
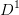
共包含6个样本{1,4,6,10,13,17}
,其中正例占

,反例占
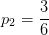
。
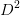
包含6个样本{2,3,7,8,9,15}
,其中正例占
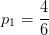
,反例
占
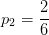
。
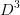
包含了5个样本{5,11,12,14,16}
,其中正例占
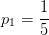
,反例占
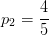
。因此,可以计算出用“色泽”划分之后所获得的3个分支结点的信息熵为:
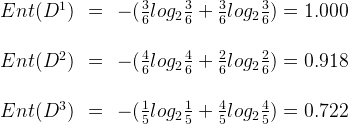
因此,特征“色泽”的信息增益为:
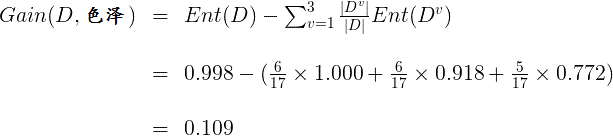
同理可以计算出其他特征的信息增益:

比较发现,特征“纹理”的信息增益最大,于是它被选为划分属性。因此可得:
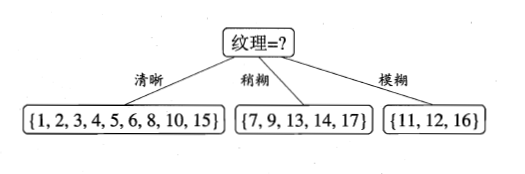
第二步、继续对上图中每个分支进行划分,以上图中第一个分支结点{“纹理=清晰”}为例,对这个结点进行划分,设该结点的样本集
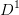
{1,2,3,4,5,6,8,10,15},共9个样本,可用特征集合为{色泽,根蒂,敲声,脐部,触感},因此基于
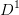
能够计算出各个特征的信息增益:

比较发现,“根蒂”、“脐部”、“触感”这3个属性均取得了最大的信息增益,可以随机选择其中之一作为划分属性(不防选择“根蒂”)。因此可得:
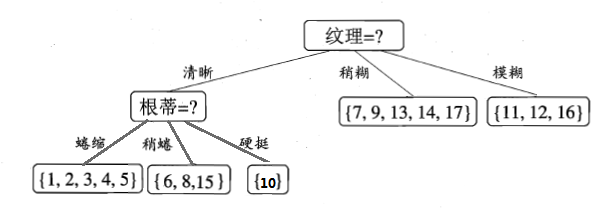
第三步,继续对上图中的每个分支结点递归的进行划分,以上图中的结点{“根蒂=蜷缩”}为例,
设该结点的样本集为{1,2,3,4,5},共5个样本,
但这5个样本的class label均为“好瓜”,因此当前结点包含的样本全部属于同一类别无需划分,将当前结点标记为C类(在这个例子中为“好瓜”)叶节点,递归返回。
因此上图变为:
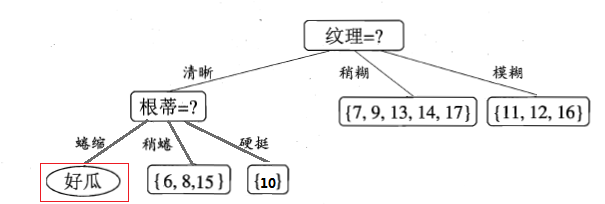
第四步,接下来对上图中结点{“根蒂=稍蜷”}进行划分,该点的样本集为
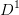
{6,8,15},共有三个样本。可用特征集为{
色泽,敲声,脐部,触感
},同样可以基于
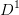
计算出各个特征的信息增益,计算过程如下(
写的比较详细,方便大家弄懂
):

(注:该图片版权所有,转载或使用请注明作者(天泽28)和出处)
不妨选择“色泽”属性作为划分属性,则可得到:
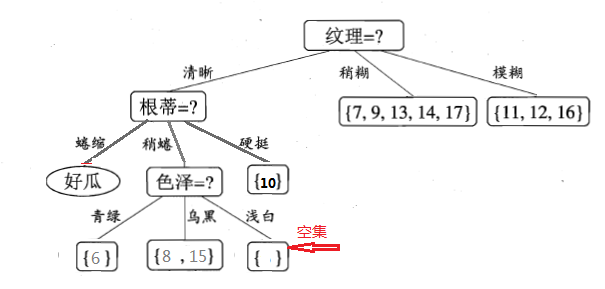
继续递归的进行,看“色泽=青绿”这个节点,只包含一个样本,无需再划分了,直接把当前结点标记为叶节点,类别为当前样本的类别,即好瓜。递归返回。
然后对递归的对“色泽=乌黑”这个节点进行划分,就不再累述了。
说下“色泽=浅白”这个节点,等到递归的深度处理完“色泽=乌黑”分支后,返回来处理“色泽=浅白”这个节点,因为当前结点包含的样本集为空集,不能划分,对应的处理措施为:将其设置为叶节点,类别为设置为其父节点(根蒂=稍蜷)所含样本最多的类别,“根蒂=稍蜷”包含{6,8,15}三个样本,6,8为正样本,15为负样本,因此“色泽=浅白”结点的类别为正(好瓜)。
最终,得到的决策树如下图所示:
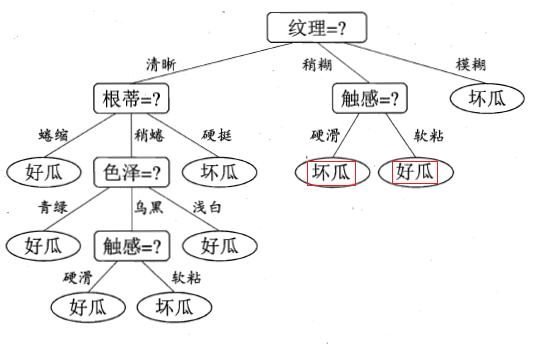
注:上图红色框起来的部分,是西瓜书印刷错误,上图已改正。周老师在他的勘误网站也有说明,详见
勘误网站
说了这么多,下面就来看看用决策树算法跑出来的效果,本人主要用weka的ID3算法(使用的信息增益),以供大家参看,后面还会放出自己实现的版本,后面再说。(之所以不要sklearn库里的决策树,是因为sklearn库里的决策树提供的是使用Gini指数优化后的CART,并不提供ID3和C4.5算法)。
由于新版本weka里已经不再提供ID3算法了,只能下载另外的安装包,把下载方法也贴出来吧,打开weka的Tools->package manager
在里面找到包simpleEducationalLearningSchemes安装即可。安装好后就可以把西瓜数据集2.0来测试了,不过要想在weka中构建模型,还要先把.txt格式转换为.arff格式,转换的代码以及转换好的数据集,详见
github
。
另外
simpleEducationalLearningSchemes提供的ID3并不像J48那样支持可视化,因此参考
链接
基于以前weka老版本写的可视化,但该代码在新版本中无法使用,我修改了下整合到ID3上了,现在可以支持可视化了,测试西瓜数据集,生成的可视化树如下,具体代码也放到了
github
上,有兴趣的可以看看。
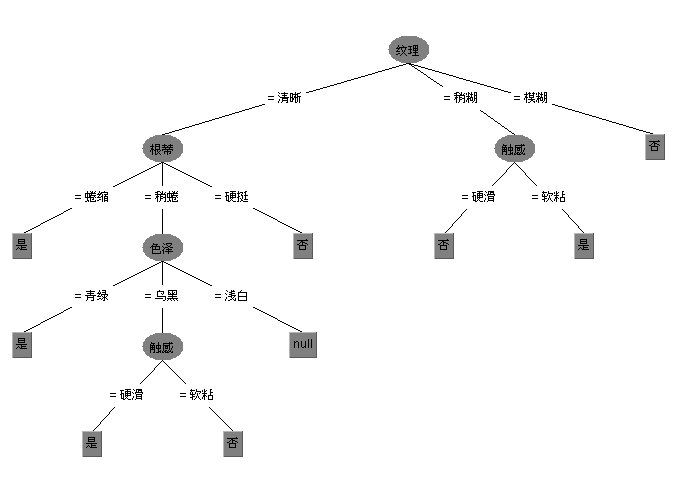
但信息增益有个缺点就是对可取数值多的属性有偏好,举个例子讲,还是考虑西瓜数据集,如果我们把“编号”这一列当做属性也考虑在内,那么可以计算出它的信息增益为0.998,远远大于其他的候选属性,因为“编号”有17个可取的数值,产生17个分支,每个分支结点仅包含一个样本,显然这些分支结点的纯度最大。但是,这样的决策树不具有任何泛化能力。
还是拿西瓜数据集2.0来测试下,如果考虑编号这一属性,看看ID3算法会生成一颗什么样的决策树:
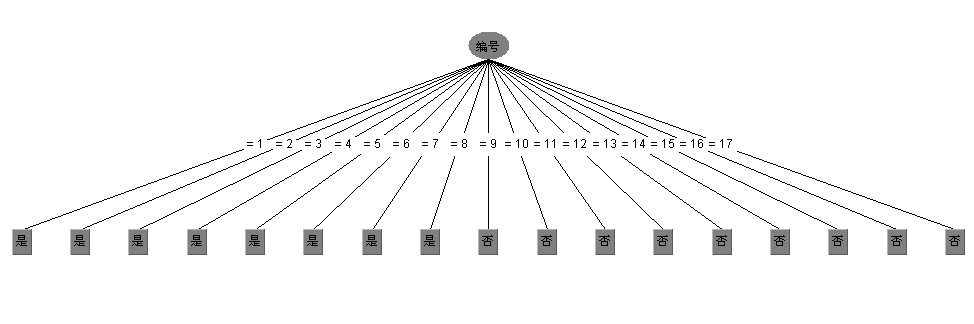
显然是生成了一颗含有17个结点的树,这棵树没有任何的泛化能力,这也是ID3算法的一个缺点。另外补充一下ID3算法的详细情况:
-
Class for constructing an
unpruned
decision tree based on the ID3 algorithm.
-
Can only deal with nominal attributes. No missing values allowed.
-
Empty leaves may result in unclassified instances. For more information see: R. Quinlan (1986). Induction of decision trees. Machine Learning. 1(1):81-106.
由于ID3算法的缺点,Quinlan后来又提出了对ID3算法的改进C4.5算法(在weka中为J48),C4.5使用了
信息增益率
来构造决策树,此外C4.5为了避免过拟合,还提供了剪枝的功能。C4.5还能够处理连续值与缺失值。剪枝与连续值和缺失值的处理在下一篇博客中再介绍。先来看看信息增益率:
-
信息增益率
信息增益比的定义为:
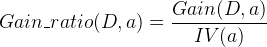
其中:
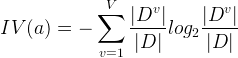
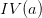
称为属性

的“固有值”,属性

的可能取值数目越多(即V越大),则
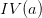
的值通常会越大。例如还是对西瓜数据集,IV(触感)=0.874(v=2),IV(色泽)=1.580(V=3),IV(编号)=4.088(V=17)。
但增益率也可能产生一个问题就是,对可取数值数目较少的属性有所偏好。
因此,C4.5算法并不是直接选择使用增益率最大的候选划分属性,而是使用了一个启发式算法:
先从候选划分属性中找出
信息增益
高于平均水平的属性
,再从中选择
信息增益率
最高的。来看看C4.5在西瓜数据集上构造的决策树:
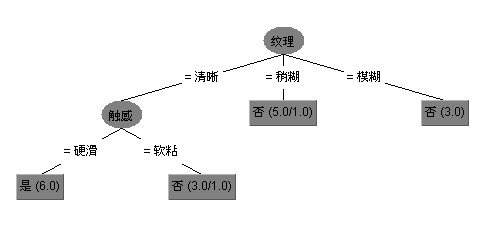
来看下混淆矩阵(Confusion Matrix)

有两个样本被误分类了。
另外还可以用基尼指数来构造决策树,像CART就是用基尼指数来划分属性的,来看下基尼指数:
-
基尼指数
基尼指数(Gini index)也可以用于选择划分特征,像CART(classification and regression tree)决策树(分类和回归都可以用)就是使用基尼指数来选择划分特征。基尼值可表示为:
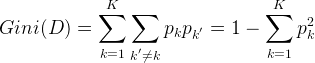
注:上面这个公式的推导可以写一下:
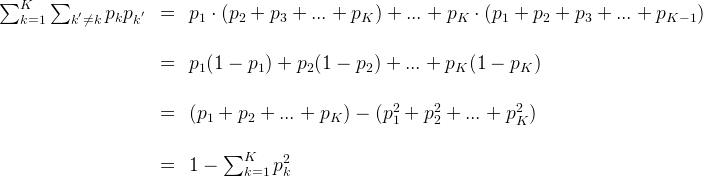
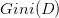
反应了从数据集D中随机抽取两个样本,其类别标记不一致的概率,因此,
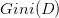
越小,则数据集D的纯度越高。则属性

的基尼指数定义为:
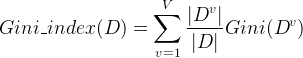
所以在候选属性集合中国,选择那个使得划分后基尼指数最小的属性作为最优划分属性。
下面是用python的scikit-learn库中提供的CART在西瓜数据集上的测试效果:
17个样本全部拿来当做训练集:
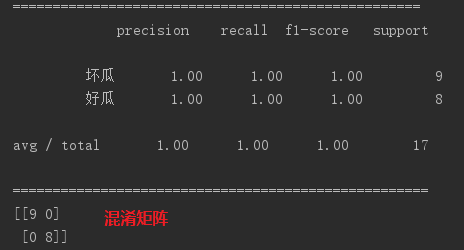
拿出25%的样本当做测试集:
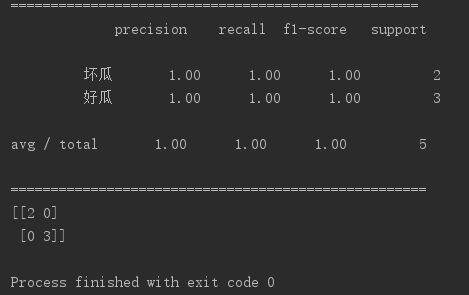
欢迎大家留言交流讨论。
|
ps:一直觉得博客不应写的太长,不然看着很累,如果知识点确实很多,则分几篇博客介绍。所以关于决策树最最基本的先写这么多,关于剪枝(预剪枝和后剪枝)将在
决策树(二)
中介绍,连续属性和缺失值处理会在决策树(三)中介绍。
版权声明:本文为u012328159原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。