最近做一个机器人采用差速驱动的原理,故总结一下关于差速驱动相关计算。
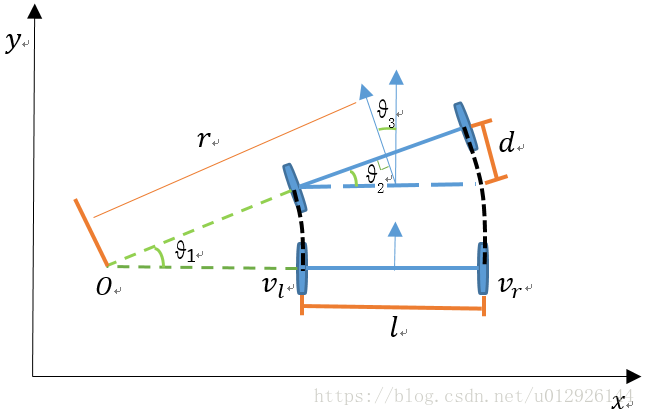
下图是移动机器人在两个相邻时刻的位姿,其中是两相邻时刻移动机器人绕圆弧运动的角度,
是两相邻时刻移动机器航向角(朝向角head)的变化量。Ldist(Vl*△t)表示左轮移动距离,Rdist(Vr*△t)代表右轮移动的距离,d是右轮比左轮多走的距离,
是左右轮之间的间距。
是移动机器人圆弧运动的半径
移动机器人前进速度等于左右轮速度的平均
![]()
几何关系可以看出
机器人在这个时间断位移很小(图中只是为了方便展示而进行的放大化处理),将机器人左右轮的前进时弧线近似为直线,故可以有
所在的近似三角求得(近似公式):
![]()
![]()
根据角速度与线速度的关系可以求得机器人绕圆心的旋转半径:

故最后可得到的公式为以下三个
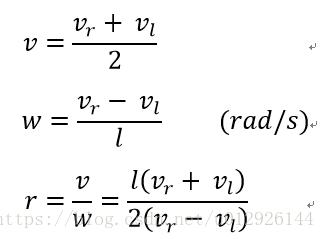 (1)
(1)
换种表示方式:
θ=(Rdist-Ldist)/l (2)
同时机器人的圆弧半径 (根据上面r的计算公式(1)中和(2))
r=(rdist+Ldist)/2*θ
故相对于初始位置x和y方向上的偏移为
deltaY=r*sinθ
deltaX=r*(1-cosθ)
下面双轮差动模型的里程计计算
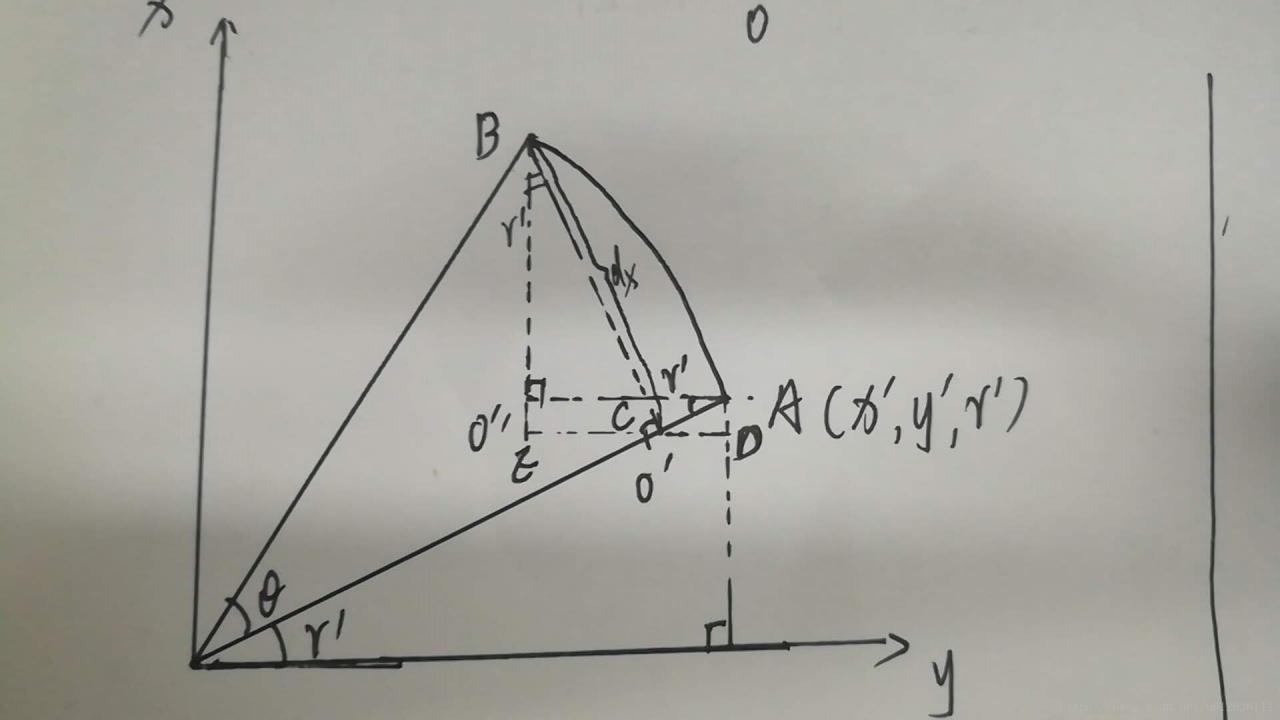
如图A((x’, y’, r’)) B(x, y, r),机器人由A移动到B,则
在图中(注意坐标系的建立与上面的不同),O’A=delatX, O’B=deltaY。
由A到B在x方向的位移变化主要是O”A可在三角形O’BE和O’AD中计算为BE-AD。
在Y方向的变化主要是O”A。
主要参考:
https://blog.csdn.net/heyijia0327/article/details/47021861
http://ai.ustc.edu.cn/cn/seminar/files/2012/navigation.pdf
全文很粗糙有的地方很简单,禁止转载