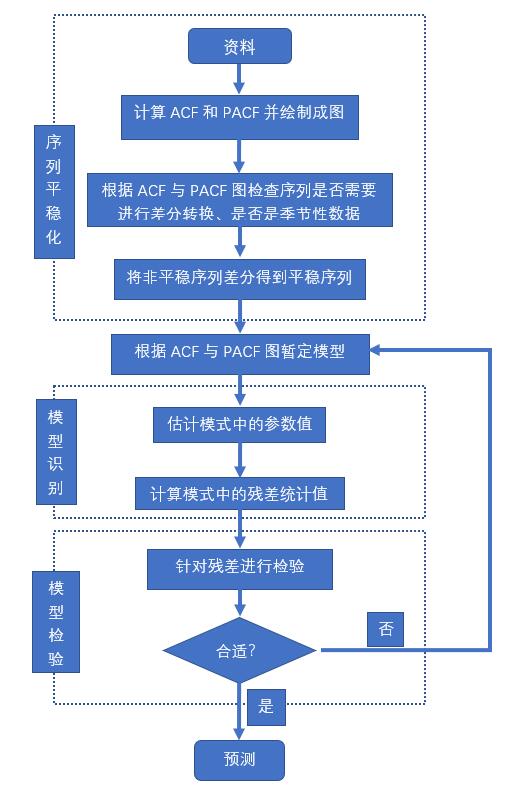
ARIMA模型运用的流程
- 根据时间序列的散点图、自相关函数和偏自相关函数图识别其平稳性。
- 对非平稳的时间序列数据进行平稳化处理。直到处理后的自相关函数和偏自相关函数的数值非显著非零。
- 根据所识别出来的特征建立相应的时间序列模型。平稳化处理后,若偏自相关函数是截尾的,而自相关函数是拖尾的,则建立AR模型;若偏自相关函数是拖尾的,而自相关函数是截尾的,则建立MA模型;若偏自相关函数和自相关函数均是拖尾的,则序列适合ARMA模型。
- 参数估计,检验是否具有统计意义。
- 假设检验,判断(诊断)残差序列是否为白噪声序列。
-
利用已通过检验的模型进行预测。
自相关函数(不同数据类型定义不同):https://zh.wikipedia.org/wiki/自相关函数。
平稳序列的定义
(在不同的时间间隔)
- 均值是常数
- 有恒定的方差或标准差。
- 自协方差不应依赖于时间
为什么要求时间序列是平稳的
- 如果时间序列是平稳的,那么在一段时间内有一个特定的行为, 那么可能在下一段时间内也有特定的行为,这样的特性有助于准确预测。
- 预测平稳时间序列的理论和数学公式更加成熟。
如何判断时间序列是否平稳
- 滚动统计—绘制移动平均线或移动标准差,看看它是否随时间而变化。这是一种视觉技巧。
- ADCF测试—假设检验,零假设为时间序列是非平稳的,设定检验统计量,如果检验统计量小于临界值(实验结果发生是小概率事件),则可以拒绝零假设,认为序列是平稳的。
假设检验
- 是依据一定的假设条件由样本推断总体的一种方法。
- 假设检验的基本思想是小概率反证法思想,小概率思想认为小概率事件在一次试验中基本上不可能发生,在这个方法下,我们首先对总体作出一个假设,如果在原假设下,实验结果发生的概率为小概率事件,也就是小概率事件竟然发生了,那我们就有理由怀疑原假设的真实性,从而拒绝这一假设。
如何找到ARIMA的P & Q值
我们需要借助ACF(自动相关函数)和PACF(部分自动相关函数)图。ACF和PACF图用于寻找ARIMA的P & Q值。我们需要检查,对于x轴上的哪个值,图线第一次在y轴上下降到0。
From PACF(at y=0), get P
From ACF(at y=0), get Q
指数平滑法(时间序列预测算法)
- 指数平滑法是生产预测中常用的一种方法。也用于中短期经济发展趋势预测,所有预测方法中,指数平滑是用得最多的一种。
- 指数平滑法可分为一次指数平滑法,二次指数平滑法,三次指数平滑法。一次指数平滑法预测的时间序列为一条直线,不能反映时间序列的趋势和季节性。 二次指数平滑的预测结果是一条斜的直线,使得预测的时间序列可以包含之前数据的趋势。三次指数平滑在二次指数平滑的基础上保留了季节性的信息,使得其可以预测带有季节性的时间序列。
-
一次指数平滑法的基本原理

-
指数平滑法的应用实例
https://blog.csdn.net/nieson2012/article/details/51980943 -
指数平滑法的代码分析
jupyter实验过程代码:
链接: https://pan.baidu.com/s/1i6WLH6t 密码: sbnb -
指数平滑法的缺点:
(1)对数据的转折点缺乏鉴别能力,但这一点可通过调查预测法或专家预测法加以弥补。
(2)长期预测的效果较差,故多用于短期预测。 -
指数平滑法的优点:
(1)对不同时间的数据的非等权处理较符合实际情况。
(2)实用中仅需选择一个模型参数a 即可进行预测,简便易行。
指数衰减法
在神经网络的参数更新过程中,学习率不能太大也不能太小,太大可能会导致参数在最优值两侧来回移动,太小会大大降低优化速度,为了解决学习率的问题,TensorFlow 提供了一种灵活的学习率设置方法,即指数衰减法。x表示迭代部署,y表示学习率。
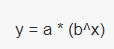
版权声明:本文为weixin_43730955原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。