1.题目
地图上有
N
N
N
个目标,用整数
X
i
,
Y
i
Xi,Yi
X
i
,
Yi
表示目标在地图上的位置,每个目标都有一个价值
W
i
Wi
Wi
。
注意
:不同目标可能在同一位置。
现在有一种新型的激光炸弹,可以摧毁一个包含
R
×
R
R×R
R
×
R
个位置的正方形内的所有目标。
激光炸弹的投放是通过卫星定位的,但其有一个缺点,就是其爆炸范围,即那个正方形的边必须和 x,y 轴平行。
求一颗炸弹最多能炸掉地图上总价值为多少的目标。
输入格式
第一行输入正整数
N
N
N
和
R
R
R
,分别代表地图上的目标数目和正方形包含的横纵位置数量,数据用空格隔开。
接下来
N
N
N
行,每行输入一组数据,每组数据包括三个整数
X
i
,
Y
i
,
W
i
Xi,Yi,Wi
X
i
,
Yi
,
Wi
,分别代表目标的
x
x
x
坐标,
y
y
y
坐标和价值,数据用空格隔开。
输出格式
输出一个正整数,代表一颗炸弹最多能炸掉地图上目标的总价值数目。
数据范围
0
≤
R
≤
109
0≤R≤109
0
≤
R
≤
109
0
<
N
≤
10000
,
0<N≤10000,
0
<
N
≤
10000
,
0
≤
X
i
,
Y
i
≤
5000
0≤Xi,Yi≤5000
0
≤
X
i
,
Yi
≤
5000
0
≤
W
i
≤
1000
0≤Wi≤1000
0
≤
Wi
≤
1000
输入样例:
2 1
0 0 1
1 1 1
输出样例:
1
2.基本思想
思路:
二维前缀和
只需要0(N
2
)递推求出二维前缀和S,然后0(N
2
)枚举边长为R的正方形的右下角坐标(i,j),即可通过上式O(1)计算出该该正方形内所有目标的价值之和,更新答案。
我们把(X,Y)作为一个“格子”,而原题中(X,Y)是一个点,并且正方形边上的目标不会被摧毁。实际上,我们不妨认为这个点就是处于“格子“(X,Y)的中心位置,格子的左上角坐标为(X-0.5,Y-0.5).右下角坐标为(X+0.5,Y+0.5),而正方形的右下角处于“格线交点“上,即一个值为“x.5”的坐标。这个转化与原问题是等价的。
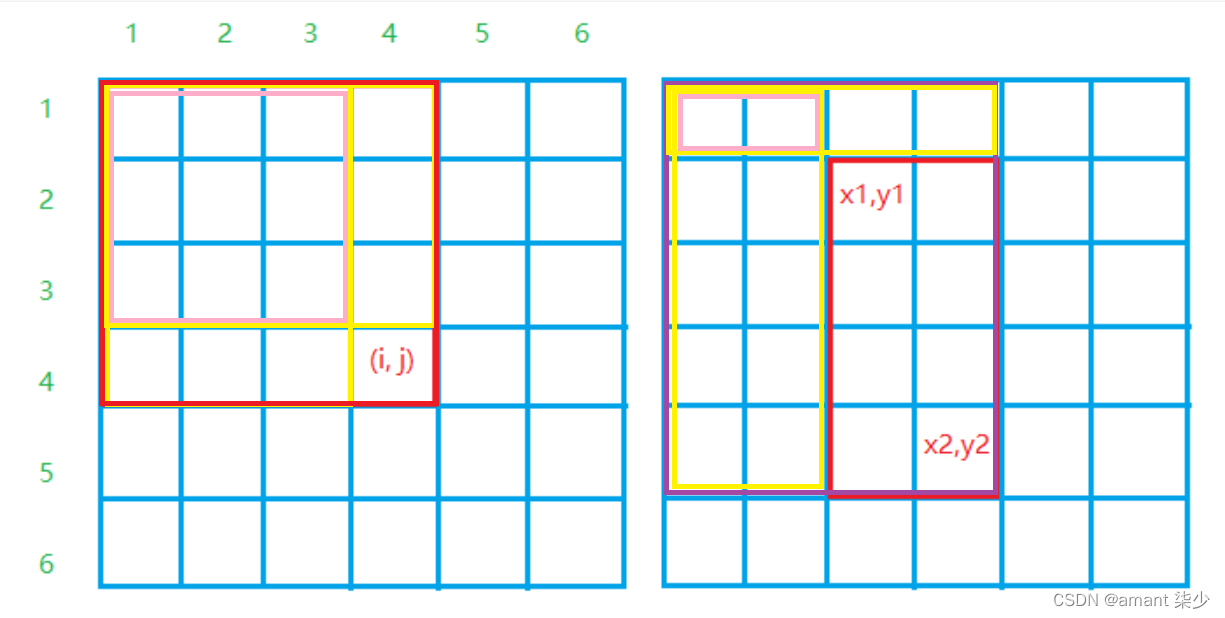
容斥原理容斥原理
容斥原理
1.
S
[
i
,
j
]
即为图
1
红框中所有数的的和为:
1.S[i,j]即为图1红框中所有数的的和为:
1.
S
[
i
,
j
]
即为图
1
红框中所有数的的和为:
S
[
i
,
j
]
=
S
[
i
,
j
−
1
]
+
S
[
i
−
1
,
j
]
−
S
[
i
−
1
,
j
−
1
]
+
a
[
i
,
j
]
S[i,j]=S[i,j−1]+S[i−1,j]−S[i−1,j−1]+a[i,j]
S
[
i
,
j
]
=
S
[
i
,
j
−
1
]
+
S
[
i
−
1
,
j
]
−
S
[
i
−
1
,
j
−
1
]
+
a
[
i
,
j
]
二维前缀和矩阵
2.
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
这一子矩阵中的所有数之和为:
2.(x1,y1),(x2,y2)(x1,y1),(x2,y2)这一子矩阵中的所有数之和为:
2.
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
这一子矩阵中的所有数之和为:
S
[
x
2
,
y
2
]
−
S
[
x
1
−
1
,
y
2
]
−
S
[
x
2
,
y
1
−
1
]
+
S
[
x
1
−
1
,
y
1
−
1
]
S[x2,y2]−S[x1−1,y2]−S[x2,y1−1]+S[x1−1,y1−1]
S
[
x
2
,
y
2
]
−
S
[
x
1
−
1
,
y
2
]
−
S
[
x
2
,
y
1
−
1
]
+
S
[
x
1
−
1
,
y
1
−
1
]
子矩阵
注意点
:
注意点:
注意点
:
1.R的范围远大于区间的范围,所以R最大取到5001即可
2.二维数组不能有两个,两个的话就会出现超限制内存的情况。
//最大空间:(5000*5000)2500 0000 两千五百万,若是设置两个数组(原数组与二维前缀和数组)的话,那么就会为五千万且一个int 4个字节,此时即有可达到 4 * (5 * 10
7
)约为200MB 超过指定内存空间168MB
3.代码实现
import java.util.Scanner;
public class _99激光炸弹 {
static Scanner sc = new Scanner(System.in);
public static void main(String[] args) {
int N = sc.nextInt();//目标数
int R = Math.min(5001, sc.nextInt());//半径
int s[][] = new int[5010][5010];
while (N-- > 0) {
int x = sc.nextInt();
int y = sc.nextInt();
int w = sc.nextInt();
s[++x][++y] += w;//++x来处理数据由0开始 转为1开始
}
//二维前缀和数组
for (int i = 1; i <= 5001; i++)
for (int j = 1; j <= 5001; j++)
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + s[i][j];
//求边长为R的正方形得到的最大值
int res = 0;
for (int i = R; i <= 5001; i++)
for (int j = R; j <= 5001; j++)
//枚举子矩阵 右下角 (i,j)
res = Math.max(res, s[i][j] - s[i - R][j] - s[i][j - R] + s[i - R][j - R]);
System.out.println(res);
}
}