基本概念
PPO
PPO算法和TRPO算法一样,也是一样常用的策略优化方法。与TRPO不同,PPO算法使用自适应KL惩罚系数
β
\beta
β
来约束KL散度,并且在每次策略更新中动态设置惩罚系数
β
\beta
β
;PPO算法还有另一种实现方式,不将KL散度直接放入似然函数中,而是进行一定程度的裁剪。
PPO训练过程的伪代码如下图所示:

PPO with clip
在TRPO中,使用的目标函数为:

如果令
r
t
(
θ
)
=
π
θ
(
a
t
∣
s
t
)
π
θ
o
l
d
(
a
t
∣
s
t
)
r_t(\theta)=\frac {\pi_\theta(a_t|s_t)} {\pi_{\theta_{old}}(a_t|s_t)}
r
t
(
θ
)
=
π
θ
o
l
d
(
a
t
∣
s
t
)
π
θ
(
a
t
∣
s
t
)
,那么可以得到:

上标
C
P
I
CPI
C
P
I
指的是TRPO中的保守政策迭代,如果没有约束,最大化
L
C
P
L
L^{CPL}
L
C
P
L
将会导致非常大幅度的梯度更新。为了惩罚策略的变化(即
r
t
(
θ
)
r_t(\theta)
r
t
(
θ
)
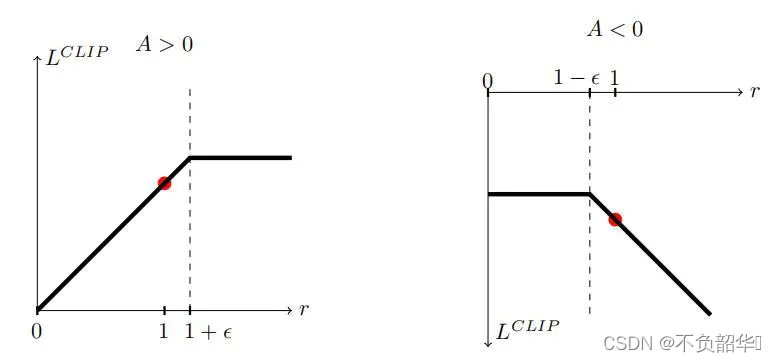
远离1,即新旧策略的KL散度不能太大),PPO算法提出了如下的目标函数:

如果新策略和旧策略之间的概率比落在区间 (1-
ϵ
\epsilon
ϵ
)和 (1 +
ϵ
\epsilon
ϵ
)外面,那么优势函数就会被剪贴。论文中
ϵ
=
0.2
\epsilon=0.2
ϵ
=
0
.
2
,直观示意图如下:
PPO with clip的算法伪代码如下图所示:

PPO with penalty
在这种形式下,PPO算法和TRPO算法的优化问题相同:
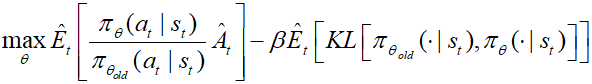
TRPO算法与PPO算法之间的区别在于TRPO算法使用了KL散度作为约束条件,而PPO算法在训练时可以采用适应性的KL惩罚因子。



在每次策略更新时,当KL散度过大时,增大
β
\beta
β
的值来增加惩罚力度;当KL散度过小时,减小
β
\beta
β
值来降低惩罚力度。