单调队列
单调队列顾名思义就是具有单调性的队列,其中单调性可以单调递增也可以单调递减,并且。队首和队尾可以进行出队操作,队尾可以进行入队操作。队首元素维护的是区间的最大值或最小值
单调队列:可以头删(过期),尾删(淘汰),尾插
单调队列的形象比喻
假如某高校ACM校队每年只有一个名额去参加比赛,所以只能选出能力最强的人去参加,因为该校只有大三及其以下能够参加该比赛,所以超过该限制的人将会被淘汰。现该队有三名队员分别是张三(年级:大三,能力:9)李四(年级:大二,能力:8)王五(年级:大一,能力:6)。在这一年,因为张三能力最强所以只有张三能够参加比赛。过了一年后,张三退役(
也就是队首出队的操作
),现在队里成员信息是李四(年级:大三,能力:8)王五(年级:大二,能力:6)两人,这时候来了一个小萌新(
队尾入队
),他的信息是刘六(年级:大一,能力:10)。因为刘六的能力比李四王五强,所以在接下来不加新人的情况下,一直会是刘六参加比赛,李四王五的大学生涯不会参见比赛了(
李四王五队尾出队
)。
滑动窗口
题目描述
给出一个长度为 𝑁 的数组,一个长为 𝐾 的滑动窗口从最左移动到最右,每次窗口移动,如下图:
找出窗口在各个位置时的极大值和极小值。
输入
第一行两个数 𝑁,𝐾。
第二行有 𝑁 个数,表示数组中的元素。
输出
输出两行,第一行为窗口在各个位置时的极小值,第二行为窗口在各个位置时的极大值。
样例输入
8 3
1 3 -1 -3 5 3 6 7
样例输出
-1 -3 -3 -3 3 3
3 3 5 5 6 7
数据规模与约定
时间限制:1 s
内存限制:256 M
100% 的数据保证 1≤𝑁≤300000
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
#include <stack>
#include <algorithm>
#include <string>
#include <map>
#include <set>
#include <vector>
using namespace std;
#define MAX_N 300000
int a[MAX_N + 5];
int q[MAX_N + 5], head = 0, tail = 0;
int main() {
int n, k;
cin >> n >> k;
for (int i = 1; i <= n; i++) cin >> a[i];
for (int i = 1; i <= n; i++) {
while (tail - head && a[q[tail - 1]] >= a[i]) tail--; //队尾出队
q[tail++] = i; //队尾入队
if (q[head] <= i - k) head++; //队首入队
if (i < k) continue;
i == k || cout << " ";
cout << a[q[head]];
}
cout << endl;
head = tail = 0;
for (int i = 1; i <= n; i++) {
while (tail - head && a[q[tail - 1]] <= a[i]) tail--;
q[tail++] = i;
if (q[head] <= i - k) head++;
if (i < k) continue;
i == k || cout << " ";
cout << a[q[head]];
}
cout << endl;
return 0;
}
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k) {
vector<int> q(nums.size(),0);
vector<int> vec;
int tail = 0, head = 0;
for(int i = 0;i< nums.size();i++){
//淘汰操作
while(tail - head && nums[i] > nums[q[tail-1]]) tail--;
//尾插操作
q[tail++] = i;
//过期头删操作
if(i - q[head] >= k) head++;
if(i < k-1) continue;
vec.push_back(nums[q[head]]);
}
return vec;
}
};
洛谷P1714 切蛋糕
该问题涉及前缀和以及单调队列问题
#include<iostream>
using namespace std;
int sum[500000],q[500000];
int main(){
int n,m,ans;
cin >> n >> m;
for(int i = 1; i <= n; i++){
cin >> sum[i];
sum[i] += sum[i-1];
}
ans = sum[1];
int tail = 0, head = 0;
// q[tail++] = 0;
for(int i = 1; i <= n; i++){
ans = max(ans,sum[i] - sum[q[head]]);
while(tail - head && sum[i] <= sum[q[tail-1]]) tail--;
q[tail++] = i;
if(i - q[head] >= m) head++;
}
cout << ans << endl;
return 0;
}
单调栈
单调栈就是从数组中找到左右两边比你大的数或者比你小的数而且时间复杂度为O(N)
单调栈与单调队列的唯一区别就是单调栈没有头删操作(过期)
单调栈与单调队列性质类似通俗的说就是具有单调性的栈,其中单调性可以单调递增也可以单调递减,并且,队尾可以进行出队操作,队尾可以进行入队操作。
单调递增栈就是从栈底到栈顶是从小到大
单调递减栈就是从栈底到栈顶是从大到小
单调队列:擅长维护区间最大/最小值,最小值对应着递增队列,最大值对应着递减队列
单调栈::擅长维护最近大于/小于关系,从左侧先入栈就是维护左侧最近关系,从右侧先入栈就是维护右侧最近关系
单调栈模板
寻找最近大于关系维护单调递减栈
stack<int> s;
for (遍历这个数组)
{
//当判断是栈顶元素小于当前元素为单调递减栈,相反为单调递增栈
while (栈不为空 && 栈顶元素小于当前元素)
{
栈顶元素出栈;
更新结果;
}
当前数据入栈;
}
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& T) {
stack<int> s;
vector<int> v(T.size(),0);
for(int i = 0; i < T.size(); i++) {
while(!s.empty() && T[s.top()] < T[i]){
v[s.top()] = i-s.top();
s.pop();
}
s.push(i);
}
return v;
}
};
class Solution {
public:
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
vector<int> res;
unordered_map<int, int> mp;
stack<int> sk;
for(int n: nums2){
//因为要找下一个比它大的元素,要维护单调递增栈
while(!sk.empty() && sk.top() < n){
mp[sk.top()] = n;
sk.pop();
}
sk.push(n);
}
while(!sk.empty()){
mp[sk.top()] = -1;
sk.pop();
}
for(int n: nums1){
res.push_back(mp[n]);
}
return res;
}
};
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
stack<int> s;
vector<int> v(nums.size(),-1);
unordered_map<int ,int> mp;
if(nums.size() == 0) {
return v;
}
for(int i = 0; i <= 2*nums.size()-1; i++){
while(!s.empty() && nums[s.top()] < nums[i%nums.size()]){
v[s.top()] = nums[i%nums.size()];
s.pop();
}
s.push(i%nums.size());
}
/* for(int i = 0; i < nums.size(); i++){
v.push_back(mp[i]);
}*/
return v;
}
};
class Solution {
public:
vector<int> dailyTemperatures(vector<int>& T) {
stack<int> s;
vector<int> v(T.size(),0);
for(int i = 0; i < T.size(); i++) {
while(!s.empty() && T[s.top()] < T[i]){
v[s.top()] = i-s.top();
s.pop();
}
s.push(i);
}
return v;
}
};
最大矩形面积
题目描述
给定从左到右多个矩形,已知这此矩形的宽度都为 1,长度不完全相等。这些矩形相连排成一排,求在这些矩形包括的范围内能得到的面积最大的矩形,打印出该面积。所求矩形可以横跨多个矩形,但不能超出原有矩形所确定的范围。
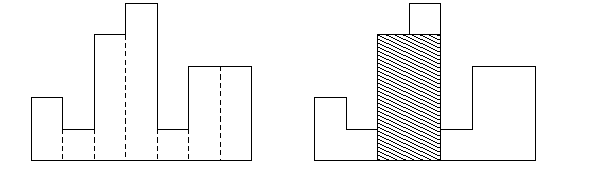
输入
输入共一行,第一个数表示矩形的个数 𝑁。接下来 𝑁 个数表示矩形的大小。(1≤𝑁≤100000)
输出
输出最大矩形面积。
样例输入
7
2 1 4 5 1 3 3
样例输出
8
数据规模与约定
时间限制:1 s
内存限制:256 M
100% 的数据保证 1≤𝑁≤100000
#include<iostream>
using namespace std;
#define max_n 100000
long long num[max_n + 5];
int l[max_n + 5];
int r[max_n + 5];
int q[max_n + 5];
int main(){
int n;
cin >> n;
for(int i = 1; i <= n; i++){
cin >> num[i];
}
int tail;
num[0] = -1;
q[tail = 0] = 0;
for(int i = 1; i <= n; i++){
while(num[i] <= num[q[tail]]) tail--;
l[i] = q[tail];
q[++tail] = i;
}
num[n + 1] = -1;
q[tail = 0] = n+1;
for(int i = n; i >= 1; i--){
while(num[i] <= num[q[tail]]) tail--;
r[i] = q[tail];
q[++tail] = i;
}
long long ans = 0;
for(int i = 1; i <= n; i++){
ans = max(ans,num[i] * (r[i] - l[i] - 1 ));
}
cout << ans << endl;
return 0;
}
#include<iostream>
using namespace std;
#define max_n 500000
int a[max_n + 5],b[max_n + 5];
int main(){
int n;
cin >> n;
for(int i = 1; i <= n; i++){
cin >> a[i];
}
for(int i = 1; i <= n; i++){
cin >> b[i];
}
int top1 = -1,top2 = -1,p;
for( p = 1; p <= n; p++){
while(top1 != -1 && a[p] <= a[top1]) top1--;
while(top2 != -1 && b[p] <= b[top2]) top2--;
if(top1 - top2) break;
a[++top1] = a[p];
b[++top2] = b[p];
}
cout << p - 1 << endl;
return 0;
}
参考:https://blog.csdn.net/lucky52529/article/details/89155694
