博客

1.行波进位加法器(ripple-carry adder)

行波进位加法器由全加器构成，也即串行进位加法器

这样我们得到加法器的结果为

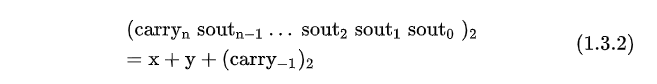
其中多出来的最低位进位carry(-1)便赋予了加法器额外再+1的能力。将式1.3.1展开得到1.4.1

得到

2. 超前进位加法器(CLA, carray lookahed adder)

它的本质是把ci中对应的gi和pi展开，得到ci与c0的直接关系。这样计算ci的时延就减少了，缺点是需要许多多操作数的与或门，对应门的扇入扇出会比较大。

为了解决上述问题，就提出了分块的方案，其中块与块之间分为串行和并行两种方案。

块内p,g之间的关系式满足

块与块之间串行：

块与块之间并行：

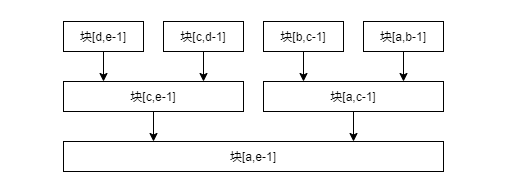
块与块之间的合并满足

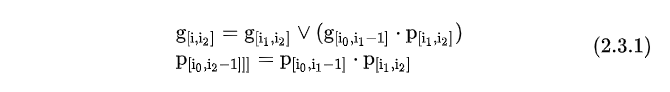
这个式子可以进一步拓展为G(R,L)=G(L)+P(L)*G®,其中L>R

3. 并行前缀加法器(PPA, parallel-prefix adder)

3.1 原理

它的本质是超前进位加法器中分块并行的实现方案。由于g,p永远都是成对出现，我们定义一个元组（g, p), 将两个块g,p信号的合并定义为并集

其中g, p之间仍然满足G(R,L)=G(L)+P(L)*G®， P(R,L)=P(L)*P®

3.2 结构

主要分为三部分，一个是根据输入计算第一层的p和g，其中p(i)=a(i)^b(i), g(i)=a(i)&b(i);

第二部分是根据第一层的p和g计算其它层的p和g

第三部分是根据p和g计算最终的结果carray和sum



c(i)=g(i)+p(i)c(i-1)

s(i)=p(i)^c(i-1)

展开后表示为下图中的式子

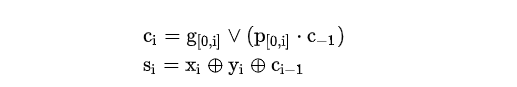
3.3 举例(4 bit）

注意：这里的ci是直接和c(-1)相关联的，但是si是和c(i-1)相关联的，意味这我们只能先计算出carray,然后才能计算出所有的sum。以4’b1111+4’b0001为例，第一层的g0=(0001) p0=(1110)；因此

Q(0,0)= (g0, p0)=(1,0)

Q(0,1) = Q(1,1)+Q(0,0)=(0,1)+(1,0) = (0+1*1, 1+0)=(1,0)

Q(0,2)=Q(2,2)+Q(0,1)=(0,1)+(1,0)=(1,0)

Q(0,3)=Q(3,3)+Q(0,2)=(0,1)+(1,0)=(1,0)

因此g[0,i]=(1,1,1,1), p[0,i]=(0,0,0,0)

由于c(-1)=0,因此ci = g[0,i]+(p[0,i]*c(-1))=g[0,i]=(1,1,1,1)

si = xi ^ yi ^ c(i-1)=p0 ^ c(i-1)= (1110)^(11110) =(10000),c(-1)=0， 结果正确

如果c(-1)=1,则ci = g[0,i]+p[0,i]=(1,1,1,1)

si=xi ^ yi ^ c(i-1)=p0 ^ c(i-1)=(1110)^(11111)=(10001), c(-1)=1, 结果正确。

3.4 并行前缀图

下图是上面例子中用到的前缀图，相当于一个行波进位加法器

kogge-stone(kS)结构

Brent-Kung (BK)结构

BK结构的并行前缀网络如上图3.6所示。它的特点是扇出非常小，节点也较少，但逻辑级数更多。BK结构是通过增加额外的逻辑级数来缓解扇出压力的

4. flag prefix adder

4.1 原理

通过一个电路可以计算A+B或者A+B+1

图中的f表示为

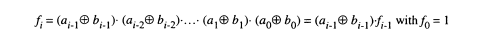
从上面这个图可以得到R=S^F

invert flagged sum bits指的是如果f(i)=1,这对sum进行取反，相当于和f进行异或，得到sum+1;invert all the sum bits, 对所有sum bit 进行取反，如果再加1表示-(A+B)，现在没有加1，则表示-(A+B)-1=-(A+B+1);

如果对B进行取反，然后运算，正常算出来的值为A-B-1;如果和flag进行异或，算出来的值为A-B;如果对sum进行取反，则算出来的值为B-A;

4.2 结构

其中e0表示翻转flagged bits 对应的sum;e1表示翻转unflagged bits 对应的sum。我认为模块是可以输出sum和r(0:w)的，所以有两个输出，或者是将overflow对应到e0,直接进行选择输出。

如果e1=e2=0,则p(i+1)保持不变，不管f(i+1)是什么，r(i+1)=A+B，这里比dual adder应该路径延时要大一些，如果dual adder,可以直接根据是否overflow进行选择sum，sum+1, 但是图中的模式，overflow选择信号需要对应转为e0,e1, 后续进行运算得到sum和sum+1的结果。

由于fi和ci不可能同时拉高，因此ci的异或只可能在f(i)=0的分支上，因此我们可以对figure4进行调整。

因此，如果e1为0，则可以得到A+B和A+B+1

如果e0=0,则可以得到A+B和-(A+B+2)

参考链接：

https://zhuanlan.zhihu.com/p/387639241

The “flagged prefix adder” for dual additions