博客

01背包 暴力解法

01背包问题正如其名，其本质就是真和假，0和1。每个物品只有要么被装进背包，要么没有装进背包这两种状态。其暴力解法也算是一种全排列问题。

如上图所示，我们可以用一个数组used来表示这五个物品当前的状态。{0,0,0,0,0}该数组就表示这五个物品都没有被选中。{1,0,0,0,0}表示只有第一个物品被选中了。

第一步 找到所有的可能性

便是找到所有的可能性，其总数为 C

⁰


₅

+ C

¹


₅

+ C

²


₅

+ C

³


₅

+ C

⁴


₅

+ C

⁵


₅

= 2

⁵

= 32 。也就是找出其全排列。


具体解题细节我写在注释里了

/**
     * 计算全排列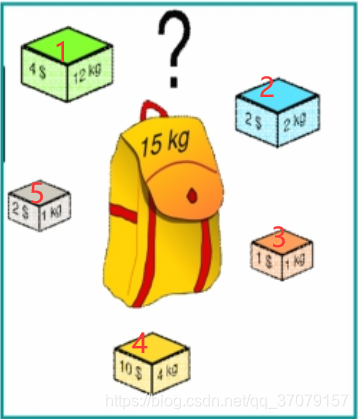![在这里插入图片描述](https://img-blog.csdnimg.cn/20201104173601395.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3FxXzM3MDc5MTU3,size_16,color_FFFFFF,t_70#pic_center)

     * @param res 存储所有的全排列（所有的可能性）
     * @param path 存储一条可能性
     * @param depth 目前递归的深度
     * @param len 总深度
     */
public static void giveBack(List<List<Integer>> res, Deque<Integer> path, int depth, int len){
        if (depth>=len){ //递归终止的条件
            res.add(new ArrayList<>(path));// new ArrayList<>(path)  === path.clone() 相当于创建了一个path的副本。具体原因在下面说明。
            return;
        }
        path.add(0); //压进path;
        giveBack(res,path,depth+1,len);
        path.removeLast();//在递归完之后，从path中弹出，恢复为上一个状态。
        
        path.add(1);//压进path;
        giveBack(res,path,depth+1,len);
        path.removeLast();//在递归完之后，从path中弹出，恢复为上一个状态。
        return;
    }

new ArrayList<>(path) === path.clone() 相当于创建了一个path的副本。

如果使用res.add(path)，path是一个引用数据类型的变量它指向了一个对象空间，res.add(path)这条语句执行之后并没有把path中的值存入res中，而是把path指向的对象空间的地址给了res。也就是说当所有的递归执行完毕之后，res数组中的所有元素全部都指向了path指向的对象空间，这就表示res数组中的值是一样的。path的最终值为{1,1,1,1,1}，所以res数组中全部的元素值都是{1,1,1,1,1}，

所以要用new ArrayList<>(path) 或path.clone()，创建一个副本，断开与path主体的联系。

第二步 计算所有的可能性

计算所有可能性的重量和价值，并且通过循环和判断找到满足条件的最优解。

具体解题细节我写在注释里了

public static void main(String[] args) {
        /*
            len是物品的总数，
            c是背包的容量，
            res 存储所有的全排列（所有的可能性）
            path 存储一条可能性
            depth 目前递归的深度
         */
        int len = 5, c = 15;  //len是物品的总数，c是背包的容量
        int[] weight = {12,2,1,4,1};
        int[] value = {4,2,1,10,2};
        List<List<Integer>> res = new ArrayList<>();
        Deque<Integer> path = new ArrayDeque<>();
        giveBack(res,path,0,len);
        List<Integer> temp;  //临时变量，提高效率
        int sumWeight = 0, // 存储一条可能性的重量和价值
            sumValue = 0,
            maxValue = 0, //存储目前找到的满足条件的最大价值。
            maxIndex = 0;//存储目前最大价值对应的那一条可能性的下标。
        for (int i = 0; i < res.size(); i++) {
            temp = res.get(i); //得到res中的一条数据
            System.out.print(temp);
            System.out.print("      ");

            for (int j = 0; j < len; j++) {//计算价值和重量
                if (temp.get(j) == 1){
                    sumValue += value[j];
                    sumWeight += weight[j];
                }
            }
            System.out.print("重量 ："+sumWeight);
            System.out.print("      ");
            System.out.print("价值 ："+sumValue);
            System.out.print("      ");
            if (sumWeight > c){  //大于容量就超重
                System.out.print("超重");
                System.out.print("      ");
            }else { //小于容量，就判断一下是不是最大价值
                if (sumValue>maxValue){ //是，就更新相关信息
                    maxValue = sumValue;
                    maxIndex = i;
                }
                System.out.print("可行");
                System.out.print("      ");
            }
            System.out.println();
            sumWeight = 0;
            sumValue = 0;
        }
        //通过最大价值可能性的下标maxIndex，找到该条记录。
        System.out.println("最大价值的可行方案" + res.get(maxIndex));
    }