我们都知道计算机是以二进制的方式来处理各项运算的,有时候还会用到八进制,十六进制数,而我们人类则是以十进制的方式来处理数据和信息的(当然,有没有大神以其他的进制来处理我们就不知道了。)
二进制数字
:0,1
八进制数字
:0,1,2,3,4,5,6,7
十进制数字
:0,1,2,3,4,5,6,7,8,9
十六进制数字
:0,1,2,3,4,5,6,7,8,9,A(10),B(11),C(12),D(13),E(14),F(15)
十进制数字转换成二进制:
例如
:
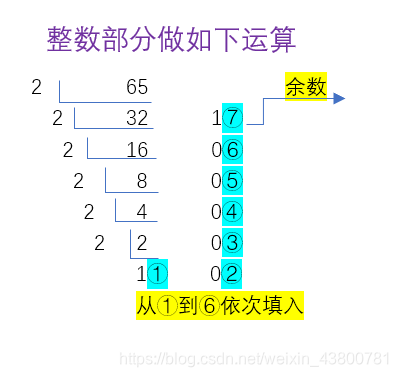
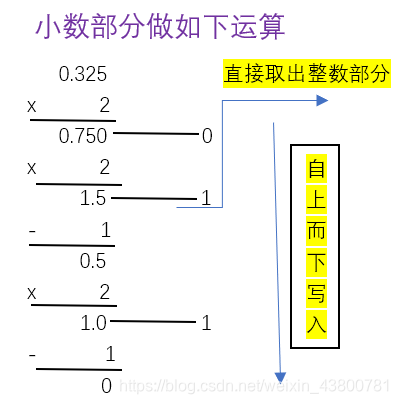
(65.325)10
=
(1000001.011)2
十进制数字转换成八进制
:
例如:
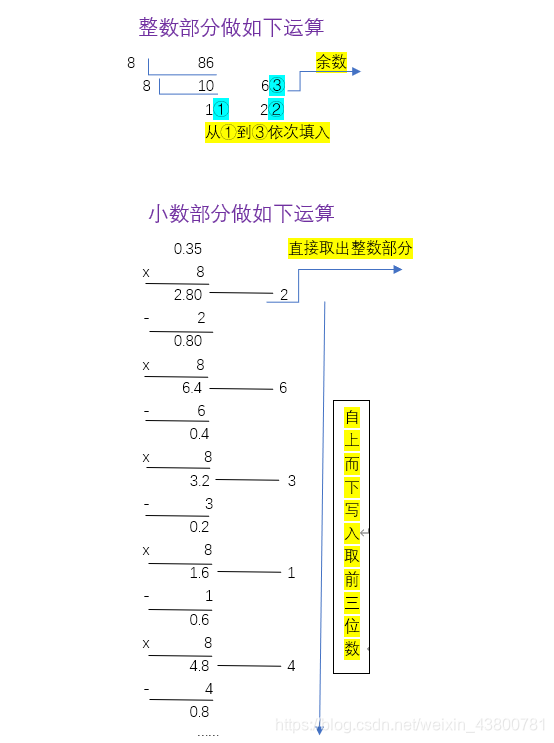
(86.35)10
=
(126.263)8
注: 一般小数部分取前三位
十进制数字转换成十六进制:
例如:
(140.95)10
=
(8C.F33)16
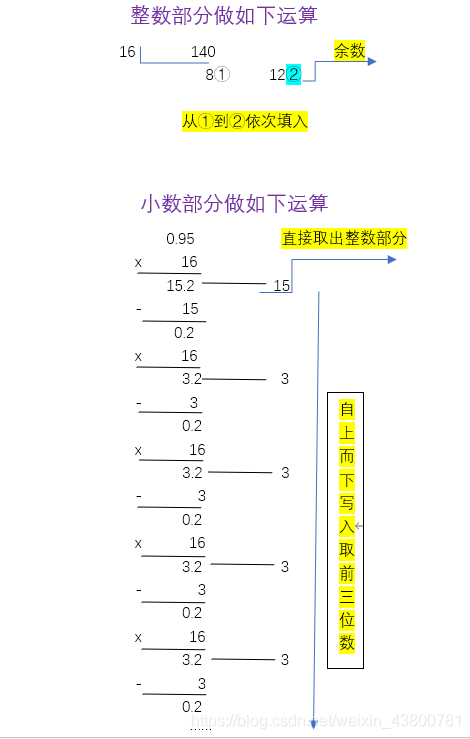
规律:十进制转换成相应进制的数字,整数部分除以对应进制取余,在除以进制在取余,依次计算下去,然后按照从下到上而写;小数部分则是乘以对应进制取整数,然后依次再乘以进制数,再取整数,有的可能无限位数,则取前三位,由上到下!
二进制准换成十进制:
例如
:
(111000.011)2
=
(56.375)10
对应位数的数字乘以相应的2的对应次幂,个位数起始为2的0次幂,整数从右往左算起,小数部分为2的负次幂乘以对应的分位数(十分位为2^-1)

二进制转换成八进制:
例如:
(111000.011)2
=
(70.3)8
111 = 2^2 X 1 + 2^1 X 1 + 2^0 X 1 = 7
000 = 2^2 X 0 + 2^1 X 0 + 2^0 X 0 = 0
011 = 2^2 X 0 + 2^1 X 1 + 2^0 X 1 = 3
学名叫做三合一法,就是从小数点开始,左面每三个为一组,不足三位用零补齐,小数点右面也是每三个一组,不足用零补齐。三个为一组用2的对应次幂乘以对应的数,从右往左依次是2^0,2^1,2^2 小数部分也是从右往左算
。
八进制转换成二进制:
逆运算就可以了,每一位数字拆开写,然后按照4(2^2) 2(2^1) 1(2^0) 的位权进行相加 ,哪个符合哪位就是1 不符合的数字就是0
比如上面的例子:
(70.3)8
=
(111000.011)2
7 = 4 + 2 + 1 = (111)2
0 = 0 + 0 + 0 = (000)2
3 = 0 + 2 + 1 = (011)2
二进制转换成十六进制
:
四合一法,和转换八进制类似,只不过是四个为一组,不足用零补齐,高位是2^3,低位是2^0,小数部分也是如此
例如:
(111000.011)2
=
(38.6)16
0011
(不足用0补齐,熟练了就不用了,自己心中有数)
=
2^3 X0 + 2^2 X 0 +2^1 X 1 + 2^0 X 1 = 3
1100 =2^3 X1 + 2^2 X 0 +2^1 X 0 + 2^0 X 0 = 8
0110
(小数部分建议补齐,有时候容易出错)
=2^3 X0 + 2^2 X 1 +2^1 X 1 + 2^0 X 0 = 6
十六进制转换成二进制:
也是逆运算,每个数字拆成四位二进制数,位权从高到低依次为8 4 2 1 符合的为1 不符合的为 0
比如上面的例子:
(38.6)16
=
(111000.011)2
对应的零可以省略
3 = 0 + 0 + 2 + 1 = (0011)2
8 = 8 + 0 + 0 + 0 = (1000)2
6 = 0 + 4 + 2 + 0 = (0110)2
八进制转成十进制:
和二进制转十进制的方法类似,因为是八进制,所以对应的位权就是8的相应次幂,算法就是对应位数的数字乘以对应的位权。
例如:
(94.25)8
=
(76.328125)10
9 x 8^1 + 4 x 8^0 + 2 x 8^-1 + 5 x 8^-2 = 72 + 4 + 0.25 + 0.078125 = 76.328125
十六进制转换成十进制:
和其他进制转成十进制类似,只不过位权是16的相应次幂,算法也是对应位数的数字乘以对应的位权
例如:
(FA.BC)16
=
(250.734375)10
15 x 16^1 + 10 x 16^0 + 11 x 16^-1 + 12 x 16^-2 = 240 + 10 + 0.6875 + 0.046875 = 250.734375
八进制转换成十六进制 和 十六进制转换成八进制 均以二进制为中介或者也可以十进制为中介