从二项分布到伽马分布
二项分布
二项分布是指
nn
n
个独立的伯努利试验中成功次数的离散概率分布,其中每次试验的成功概率为
pp
p
P
(
X
=
k
)
=
f
(
k
,
n
,
p
)
=
(
n
k
)
p
k
(
1
−
p
)
n
−
k
P(X=k)=f(k, n, p)=\begin{pmatrix}n\\k\end{pmatrix}p^k(1 – p)^{n-k}
P
(
X
=
k
)
=
f
(
k
,
n
,
p
)
=
(
n
k
)
p
k
(
1
−
p
)
n
−
k
-
kk
k
:成功的次数 -
nn
n
:总的试验次数 -
pp
p
:单词试验成功的次数
泊松分布
当二项分布试验的次数无穷多,但试验成功的总次数固定时,二项分布收敛于泊松分布。
P
(
X
=
k
)
=
e
−
λ
k
!
P(X=k)=\frac{e^{-\lambda}}{k!}
P
(
X
=
k
)
=
k
!
e
−
λ
实际意义为一段时间内试验成功的平均次数为
λ
\lambda
λ
,则同样的时间段内试验成功
k
k
k
次的概率。
简记为
X
∼
π
(
λ
)
X\sim\pi(\lambda)
X
∼
π
(
λ
)
或
X
∼
P
o
i
s
(
λ
)
X\sim Pois(\lambda)
X
∼
P
o
i
s
(
λ
)
推导:
-
已知某一固定时间长度
TT
T
内,平均会发生
λ\lambda
λ
次事件 -
将时间长度分为
nn
n
份,每一小段时间段
Tn
\frac{T}{n}
n
T
发生事件的概率为
p=
λ
n
p=\frac{\lambda}{n}
p
=
n
λ
-
则时间长度
TT
T
内,有
kk
k
次事件发生的概率为
P(
X
=
k
)
=
(
n
k
)
(
λ
n
)
k
(
1
−
λ
n
)
n
−
k
P(X=k)=\begin{pmatrix}n\\k\end{pmatrix}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k}
P
(
X
=
k
)
=
(
n
k
)
(
n
λ
)
k
(
1
−
n
λ
)
n
−
k
将时间无限细分,得到
P(
X
=
k
)
=
lim
n
→
∞
(
n
k
)
(
λ
n
)
k
(
1
−
λ
n
)
n
−
k
=
lim
n
→
∞
n
!
(
n
−
k
)
!
k
!
(
λ
n
)
k
(
1
−
λ
n
)
n
(
1
−
λ
n
)
−
k
=
lim
n
→
∞
n
!
(
n
−
k
)
!
k
!
(
λ
n
)
k
(
1
−
λ
n
)
n
=
lim
n
→
∞
n
!
(
n
−
k
)
!
n
k
λ
k
k
!
lim
n
→
∞
(
1
−
λ
n
)
n
=
(
lim
n
→
∞
n
!
(
n
−
k
)
!
n
k
)
(
λ
k
k
!
e
−
λ
)
=
(
lim
n
→
∞
n
n
n
−
1
n
⋯
n
−
k
+
1
n
)
(
λ
k
k
!
e
−
λ
)
=
λ
k
k
!
e
−
λ
\begin{align} P(X=k)&=\lim_{n\to\infin}\begin{pmatrix}n\\k\end{pmatrix}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^{n-k}\\ &=\lim_{n\to\infin}\frac{n!}{(n-k)!k!}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^n(1-\frac{\lambda}{n})^{-k}\\ &=\lim_{n\to\infin}\frac{n!}{(n-k)!k!}(\frac{\lambda}{n})^k(1-\frac{\lambda}{n})^n\\ &=\lim_{n\to\infin}\frac{n!}{(n-k)!n^k}\frac{\lambda^k}{k!}\lim_{n\to\infin}(1-\frac{\lambda}{n})^n\\ &=(\lim_{n\to\infin}\frac{n!}{(n-k)!n^k})(\frac{\lambda^k}{k!}e^{-\lambda})\\ &=(\lim_{n\to\infin}\frac{n}{n}\frac{n-1}{n}\cdots\frac{n-k+1}{n})(\frac{\lambda^k}{k!}e^{-\lambda})\\ &=\frac{\lambda^k}{k!}e^{-\lambda} \end{align}
P
(
X
=
k
)
=
n
→
∞
lim
(
n
k
)
(
n
λ
)
k
(
1
−
n
λ
)
n
−
k
=
n
→
∞
lim
(
n
−
k
)!
k
!
n
!
(
n
λ
)
k
(
1
−
n
λ
)
n
(
1
−
n
λ
)
−
k
=
n
→
∞
lim
(
n
−
k
)!
k
!
n
!
(
n
λ
)
k
(
1
−
n
λ
)
n
=
n
→
∞
lim
(
n
−
k
)!
n
k
n
!
k
!
λ
k
n
→
∞
lim
(
1
−
n
λ
)
n
=
(
n
→
∞
lim
(
n
−
k
)!
n
k
n
!
)
(
k
!
λ
k
e
−
λ
)
=
(
n
→
∞
lim
n
n
n
n
−
1
⋯
n
n
−
k
+
1
)
(
k
!
λ
k
e
−
λ
)
=
k
!
λ
k
e
−
λ
指数分布
表示独立随机事件发生的时间间隔,形式如下
f
(
x
,
λ
)
=
{
λ
e
−
λ
x
,
x
>
=
0
0
,
o
t
h
e
r
w
i
s
e
f(x,\lambda)=\begin{cases} \lambda e^{-\lambda x},&x>=0\\ 0,&otherwise \end{cases}
f
(
x
,
λ
)
=
{
λ
e
−
λ
x
,
0
,
x
>=
0
o
t
h
er
w
i
se
实际意义为已知单位时间内事件的发生次数
λ
\lambda
λ
,
X
X
X
表示从某一次事件发生之后,第
1
1
1
次事件再次发生所经历的时间。
简记为
X
∼
Exp
(
λ
)
X\sim\text{Exp}(\lambda)
X
∼
Exp
(
λ
)
推导:
-
已知单位时间内,会发生
λ\lambda
λ
次事件 -
那么单位时间内,发生
YY
Y
次事件的概率分布满足
Y∼
π
(
λ
)
Y\sim\pi(\lambda)
Y
∼
π
(
λ
)
-
则单位时间内,一次事件也没有发生的概率为
P(
Y
=
0
)
=
λ
0
0
!
e
−
λ
=
e
−
λ
P(Y=0)=\frac{\lambda^0}{0!}e^{-\lambda}=e^{-\lambda}
P
(
Y
=
0
)
=
0
!
λ
0
e
−
λ
=
e
−
λ
-
那么
xx
x
个单位时间内,其
λ′
=
λ
x
\lambda’=\lambda x
λ
′
=
λ
x
,则一次事件也没有发生的概率为
e−
λ
x
e^{-\lambda x}
e
−
λ
x
-
即
P(
X
>
x
)
=
e
−
λ
x
P(X>x)=e^{-\lambda x}
P
(
X
>
x
)
=
e
−
λ
x
,其中
XX
X
为上一次事件发生之后,到下一次事件发生所经过的时间 -
则
P(
X
≤
x
)
=
1
−
e
−
λ
x
P(X\leq x)=1-e^{-\lambda x}
P
(
X
≤
x
)
=
1
−
e
−
λ
x
-
则概率密度函数
f(
x
)
=
(
1
−
e
−
λ
x
)
′
=
λ
e
−
λ
x
f(x)=(1-e^{-\lambda x})’=\lambda e^{-\lambda x}
f
(
x
)
=
(
1
−
e
−
λ
x
)
′
=
λ
e
−
λ
x
伽马分布
假设
X
1
,
X
2
,
⋯
,
X
n
X_1,X_2,\cdots,X_n
X
1
,
X
2
,
⋯
,
X
n
为连续发生事件的等候时间,则
n
n
n
次等候时间之和
Y
=
∑
i
=
1
n
X
i
Y=\sum_{i=1}^nX_i
Y
=
∑
i
=
1
n
X
i
满足伽马分布
f
(
x
,
α
,
λ
)
=
x
(
α
−
1
)
λ
α
e
(
−
λ
x
)
Γ
(
α
)
f(x,\alpha,\lambda)=\frac{x^{(\alpha-1)}\lambda^\alpha e^{(-\lambda x)}}{\Gamma(\alpha)}
f
(
x
,
α
,
λ
)
=
Γ
(
α
)
x
(
α
−
1
)
λ
α
e
(
−
λ
x
)
或
f
(
x
,
α
,
β
)
=
x
(
α
−
1
)
e
(
−
1
β
x
)
β
α
Γ
(
α
)
f(x,\alpha,\beta)=\frac{x^{(\alpha-1)} e^{(-\frac{1}{\beta} x)}}{\beta^\alpha\Gamma(\alpha)}
f
(
x
,
α
,
β
)
=
β
α
Γ
(
α
)
x
(
α
−
1
)
e
(
−
β
1
x
)
其中
β
=
1
λ
\beta=\frac{1}{\lambda}
β
=
λ
1
。
实际意义为已知单位时间内事件平均发生次数为
λ
\lambda
λ
,
X
X
X
表示从某一次事件发生之后,第
α
\alpha
α
次事件发生所经历的时间。
简记为
X
∼
Γ
(
α
,
λ
)
X\sim\Gamma(\alpha,\lambda)
X
∼
Γ
(
α
,
λ
)
。
伽马函数介绍:
其中
Γ(
x
)
\Gamma(x)
Γ
(
x
)
为伽马函数,其形式为
Γ(
z
)
=
∫
0
∞
x
z
−
1
e
−
x
d
x
\Gamma(z)=\int_0^\infin x^{z-1}e^{-x}dx
Γ
(
z
)
=
∫
0
∞
x
z
−
1
e
−
x
d
x
通过分步积分可得
Γ(
z
)
=
∫
0
∞
x
z
−
1
e
−
x
d
x
=
∫
0
∞
x
z
−
1
d
(
−
e
−
x
)
=
x
z
−
1
(
−
e
−
x
)
∣
x
=
0
∞
+
∫
0
∞
e
−
x
(
d
x
z
−
1
)
=
(
z
−
1
)
∫
0
∞
x
z
−
2
e
−
x
d
x
=
(
z
−
1
)
Γ
(
z
−
1
)
\begin{align} \Gamma(z)&=\int_0^\infin x^{z-1}e^{-x}dx\\ &=\int_0^\infin x^{z-1}d(-e^{-x})\\ &=x^{z-1}(-e^{-x})|_{x=0}^\infin+\int_0^\infin e^{-x}(dx^{z-1})\\ &=(z-1)\int_0^\infin x^{z-2}e^{-x}dx\\ &=(z-1)\Gamma(z-1) \end{align}
Γ
(
z
)
=
∫
0
∞
x
z
−
1
e
−
x
d
x
=
∫
0
∞
x
z
−
1
d
(
−
e
−
x
)
=
x
z
−
1
(
−
e
−
x
)
∣
x
=
0
∞
+
∫
0
∞
e
−
x
(
d
x
z
−
1
)
=
(
z
−
1
)
∫
0
∞
x
z
−
2
e
−
x
d
x
=
(
z
−
1
)
Γ
(
z
−
1
)
又因为
Γ(
0
)
=
1
\Gamma(0)=1
Γ
(
0
)
=
1
,故当
xx
x
为自然数时
Γ(
x
)
=
(
x
−
1
)
!
\Gamma(x)=(x-1)!
Γ
(
x
)
=
(
x
−
1
)!
Γ(
x
)
\Gamma(x)
Γ
(
x
)
常用值有:
Γ(
1
2
)
=
π
\Gamma(\frac{1}{2})=\sqrt{\pi}
Γ
(
2
1
)
=
π
Γ(
1
)
=
1
\Gamma(1)=1
Γ
(
1
)
=
1
Γ(
3
2
)
=
π
2
\Gamma(\frac{3}{2})=\frac{\sqrt{\pi}}{2}
Γ
(
2
3
)
=
2
π
Γ(
2
)
=
1
\Gamma(2)=1
Γ
(
2
)
=
1
伽马分布的证明:
-
单位时间内发生
kk
k
次事件的概率
λk
e
−
λ
k
!
\lambda^k\frac{e^{-\lambda}}{k!}
λ
k
k
!
e
−
λ
-
xx
x
个单位时间内发生
kk
k
次事件的概率
(λ
x
)
k
e
−
λ
x
k
!
(\lambda x)^k\frac{e^{-\lambda x}}{k!}
(
λ
x
)
k
k
!
e
−
λ
x
-
xx
x
个单位时间内,发生不到
α\alpha
α
次事件的概率
∑k
=
1
α
−
1
(
λ
x
)
k
e
−
λ
x
k
!
\sum_{k=1}^{\alpha-1}(\lambda x)^k\frac{e^{-\lambda x}}{k!}
∑
k
=
1
α
−
1
(
λ
x
)
k
k
!
e
−
λ
x
-
则
P(
X
>
=
x
)
=
∑
k
=
1
α
−
1
(
λ
x
)
k
e
−
λ
x
k
!
P(X>=x)=\sum_{k=1}^{\alpha-1}(\lambda x)^k\frac{e^{-\lambda x}}{k!}
P
(
X
>=
x
)
=
∑
k
=
1
α
−
1
(
λ
x
)
k
k
!
e
−
λ
x
-
P(
X
<
x
)
=
1
−
∑
k
=
1
α
−
1
(
λ
x
)
k
e
−
λ
x
k
!
P(X<x)=1-\sum_{k=1}^{\alpha-1}(\lambda x)^k\frac{e^{-\lambda x}}{k!}
P
(
X
<
x
)
=
1
−
∑
k
=
1
α
−
1
(
λ
x
)
k
k
!
e
−
λ
x
-
对
PP
P
求导之后可得概率密度函数
f(
x
)
=
λ
e
−
λ
x
(
λ
x
)
k
−
1
(
k
−
1
)
!
=
λ
k
x
k
−
1
e
−
λ
x
Γ
(
k
)
f(x)=\frac{\lambda e^{-\lambda x}(\lambda x)^{k-1}}{(k-1)!}=\frac{\lambda^kx^{k-1}e^{-\lambda x}}{\Gamma(k)}
f
(
x
)
=
(
k
−
1
)!
λ
e
−
λ
x
(
λ
x
)
k
−
1
=
Γ
(
k
)
λ
k
x
k
−
1
e
−
λ
x
性质:
-
期望
kγ
\frac{k}{\gamma}
γ
k
,方差
kγ
2
\frac{k}{\gamma^2}
γ
2
k
-
满足可加性,若
X1
,
X
2
X_1,X_2
X
1
,
X
2
相互独立,且
X1
∼
Γ
(
α
1
,
λ
)
X_1\sim\Gamma(\alpha_1,\lambda)
X
1
∼
Γ
(
α
1
,
λ
)
,
X2
∼
Γ
(
α
2
,
λ
)
X_2\sim\Gamma(\alpha_2,\lambda)
X
2
∼
Γ
(
α
2
,
λ
)
,则
X1
+
X
2
∼
Γ
(
α
1
+
α
2
,
λ
)
X_1+X_2\sim\Gamma(\alpha_1+\alpha_2,\lambda)
X
1
+
X
2
∼
Γ
(
α
1
+
α
2
,
λ
)
-
Γ(
1
,
λ
)
=
E
(
λ
)
\Gamma(1,\lambda)=E(\lambda)
Γ
(
1
,
λ
)
=
E
(
λ
)
,
Γ(
n
2
,
1
2
)
=
χ
2
(
n
)
\Gamma(\frac{n}{2},\frac{1}{2})=\chi^2(n)
Γ
(
2
n
,
2
1
)
=
χ
2
(
n
)
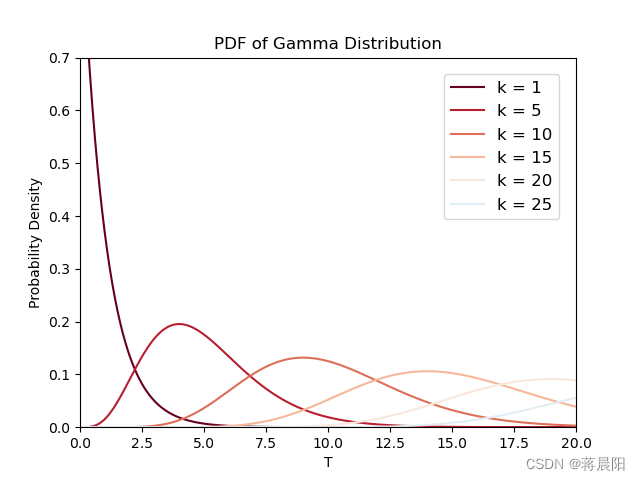
函数图像展示:
当固定
k
k
k
时,可以看到随着
λ
\lambda
λ
的增加,函数也随之增高(方差降低),同时分布靠近原点(期望降低)。因为更容易在较短的时间内发生
k
k
k
次事件。
总结
| 分布 | 含义 |
|---|---|
|
二项分布 B ( n , p ) B(n,p) B ( n , p ) |
n n n 次独立伯努利试验中事件恰发生 k k k 次的概率 |
|
泊松分布 π ( λ ) \pi(\lambda) π ( λ ) |
已知单位时间内会发生 λ \lambda λ 次事件,事件在任意时刻发生概率相同,求同样时间内发生 k k k 次事件的概率。 |
|
指数分布 Exp ( λ ) \text{Exp}(\lambda) Exp ( λ ) |
已知单位时间内会发生 λ \lambda λ 次事件,事件在任意时刻发生概率相同,求发生一次事件后,等待 t t t 个单位时间之后再次发生事件的概率密度函数 |
|
伽马分布 Γ ( α , λ ) \Gamma(\alpha,\lambda) Γ ( α , λ ) |
已知单位时间内会发生 λ \lambda λ 次事件,事件在任意时刻发生概率相同,求发生一次事件后,等待 t t t 个单位时间之后会发生第 α \alpha α 次事件的概率密度函数 |
参考链接: