博客

1.知识储备：



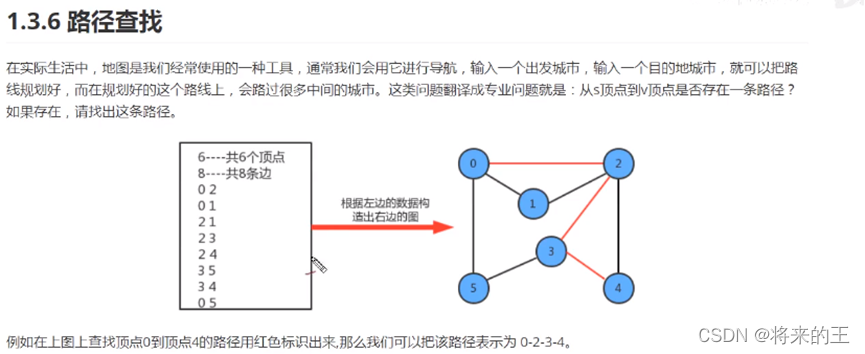
2.路径查找API：



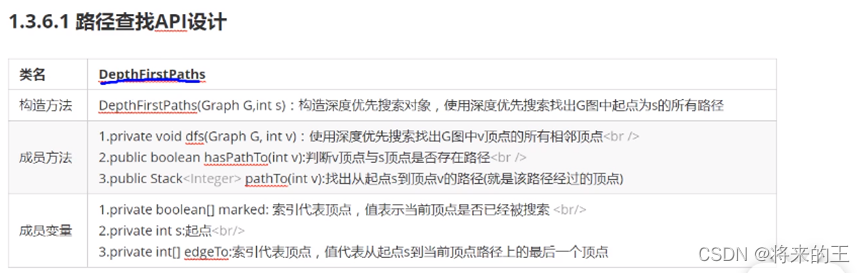
3.步骤图解：





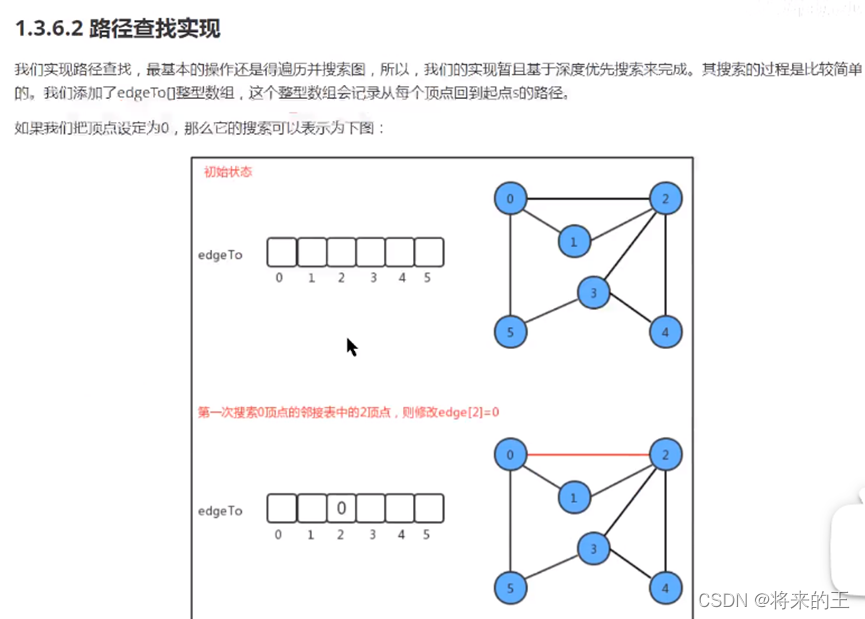
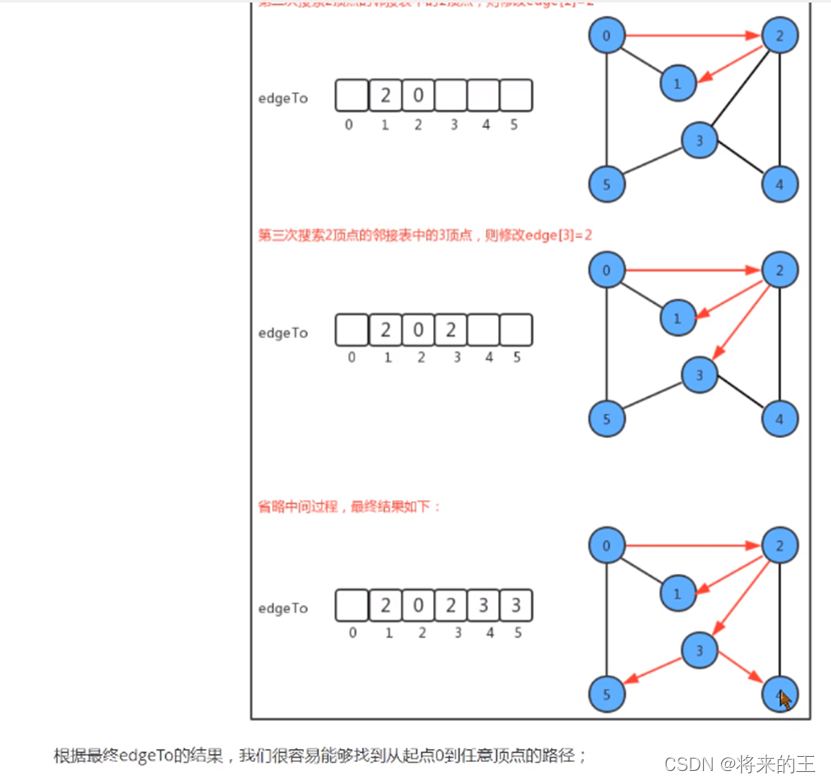
4.源码实现：

package Graph;

import Stack.Stack;

public class DepthFirstPath {
   //索引代表顶点，值表示当前顶点是否已经被搜索
	private boolean[] marked;
	//起点
	private int s;
	//索引代表顶点，值代表从从起点s到当前顶点路径上的最后一个顶点
	private int[] edgeTo;
	
	//构建深度优先搜索对象，使用深度优先搜索找出G图中起点为s的所有路径
	public DepthFirstPath(Graph G,int s){
		//初始化marked数组
		this.marked=new boolean[G.V()];
		//初始化起点
		this.s=s;
		//初始化edgeTo数组
		this.edgeTo=new int[G.V()];
		dfs(G,s);
	}
	
	//使用深度优先搜索找出G图中v顶点相邻的所有顶点
	public void dfs(Graph G,int v){
		//把v标识为已搜索
		marked[v]=true;
		//遍历顶点V的邻接表,每拿到一个相邻的顶点，继续递归搜索
		for(Integer w:G.adj(v)){
			//如果顶点w没有被搜索，则继续递归搜索
			if(!marked[w]){
				edgeTo[w]=v;//到达顶点w路径上的最后一个顶点是v
				dfs(G,w);
			}
		}
	}
	
	//判断s顶点与v顶点是否存在路径
	public boolean hasPathTo(int v){
		return marked[v];
	}
	
	//找出从起点s到顶点v的路劲（就是该路径经过的顶点）
	public Stack<Integer> pathTo(int v){
		//安全性校验
		if(!hasPathTo(v)){
			return null;
		}
		//创建栈对象，保存路径中的所有顶点
		Stack<Integer> path=new Stack<Integer>();
		//通过循环，从顶点v开始，一直往前找，找到起点为止
		for(int x=v;x!=s;x=edgeTo[x]){
			path.push(x);
		}
		//把起点放到栈中
		path.push(s);
		return path;	
	}
}

5.测试

   package Graph;

import java.io.BufferedReader;
import java.io.InputStreamReader;

import Stack.Stack;


public class DepthFirstPathTest {
     public static void main(String[] args) throws Exception{
		//构建缓冲读取流BufferedReader
    	 BufferedReader rd=new BufferedReader(new InputStreamReader(DepthFirstPathTest.class.getClassLoader().getResourceAsStream("road.txt")));
    	 //读取第一行数据6
    	 int total=Integer.parseInt(rd.readLine());
    	 //根据第一行数据构建一幅图
    	 Graph G=new Graph(total);
    	 //读取第二行数据8
    	 int edgeNumbers=Integer.parseInt(rd.readLine());
    	 //通过循环继续读取每一条边关联的两个顶点，调用addEdge方法,添加边
    	 for(int i=1;i<=edgeNumbers;i++){
    		 String edge=rd.readLine();
    		 String[] str=edge.split(" ");
    		 int v=Integer.parseInt(str[0]);
    		 int w=Integer.parseInt(str[1]);
    		 G.addEdge(v, w);
    	 }
    	 //构建路劲查找对象，并设置起点为0
    	 DepthFirstPath paths=new DepthFirstPath(G, 0);
    	 //调用pathTo(4),把从起点0到终点4的路径返回stack
    	 Stack<Integer> path=paths.pathTo(4);
    	 StringBuilder sb=new StringBuilder();
    	 //遍历栈对象
    	 for(Integer v:path){
    		 sb.append(v+" ");
    	 }
    	 sb.deleteCharAt(sb.length()-1);
    	 System.out.println(sb);
    	 
	}
}

6.运行结果：