理想相机成像模型
看到一篇博客,介绍的十分详细.参考
链接
(为了好理解,个人还是喜欢分四大坐标系,世界坐标系,摄像机坐标系,图像物理坐标系,图像像素坐标系)
1)世界坐标系->摄像机坐标系
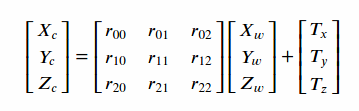
R矩阵为旋转矩阵,T矩阵为平移矩阵,RT矩阵变换,属于刚体转换,旋转矩阵具体分为世界坐标系如何分别绕x,y,z三个轴旋转多少度后坐标系方向与摄像机坐标系一致,平移矩阵则对应世界坐标系原点需如何平移至相机坐标系原点.opencv标定后每图的旋转/平移参数都是3个,应该就是对应三个轴的旋转角度alpha,beta,gama和三个方向的平移量.
齐次表达式
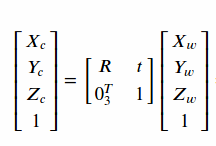
其中R矩阵由三个轴的旋转得到,如下图所示(来源黑土的Halcon学习教程)

2)摄像机坐标下->图像物理坐标系
图像物理坐标系其实可以理解为CCD芯片平面的坐标系
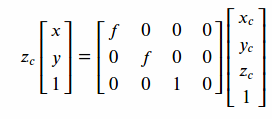
3)图像物理坐标系->图像像素坐标系
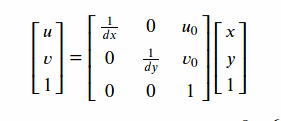
dx,dy是芯片像素单元的物理尺寸,u0,v0是光轴中心的图像像素坐标
综上得到世界坐标系->图像像素坐标系

opencv标定实验
我的想法是,按照模型原理,自己设置相机内外参数,畸变参数,生成畸变数据点,然后用opencv标定后得到的参数做一个比较.我用opencv-python写的程序如下
# -*- coding:utf-8 -*-
# @Author : ZYK
import numpy as np
import cv2
"""
这里根据相机成像模型,参考 https://www.cnblogs.com/zyly/p/9366080.html
手动构建相关参数,构建畸变像素点后,用opencv标定求解参数,最终对比.
为简化模型,世界坐标系与相机坐标系方向一致
"""
#定义基本参数
pixsize=0.1 #假设像素精度是0.1mm
imgw=1280
imgh=1024
Zc=150 #物距
f=15 #像距
row=7 #棋盘点行数
col=9#棋盘点列数
space=10 #棋盘点间隔
u0=imgw/2#光轴中心
v0=imgh/2
k1=-2e-3 #径向畸变系数(这里不考虑切向畸变)
k2=-5e-5
k3=-1e-6
chipw=imgw*pixsize*f/Zc #传感器尺寸
chiph=imgh*pixsize*f/Zc
dx=chipw/imgw #每个像素的硬件物理尺寸
dy=chiph/imgh
#构建棋盘世界坐标点(齐次坐标)
obj_point = np.zeros((4,row * col), np.float32)
for idx in range(row*col):
obj_point[:3,idx]=[idx%col*space,idx//col*space,0]
obj_point[3,:]=1
each_obj_point=obj_point[:3, :].T
#小孔成像转换矩阵
prjmat=np.array([[f,0,0,0],
[0,f,0,0],
[0,0,1,0]],np.float32)
#相机内参矩阵
kmat=np.array([[1 / dx, 0 ,u0],
[0, 1 / dy, v0],
[0, 0, 1]],np.float32)
init_rvecs=[] #旋转矩阵参数集合
init_tvecs=[]
obj_points=[]
img_points=[]
picnum=10 #模拟用于标定的图片数,这里简化每张图世界坐标系仅仅绕Z轴旋转Gama角度
Testimg=(np.ones((imgh,imgw,3))*255).astype(np.uint8)
for idx in range(picnum):
angle=np.pi/3*(np.random.rand()-0.5)#-30~30度
if idx==0:
angle=0
init_rvecs.append([0,0,angle])
src_offsetx = -(col - 1) * space / 2
src_offsety = -(row - 1) * space / 2
tvec=[src_offsetx * np.cos(angle) - src_offsety * np.sin(angle),#平移参数Tx,Ty,Tz,这里使点中心在光轴上
src_offsetx * np.sin(angle) + src_offsety * np.cos(angle),
Zc]
init_tvecs.append(tvec)
#平移旋转齐次矩阵
rtmat=np.eye(4,4,dtype=np.float32)
rtmat[0,0]=rtmat[1,1]=np.cos(angle)
rtmat[0, 1]=-np.sin(angle)
rtmat[1, 0] = np.sin(angle)
rtmat[:3,3]=tvec
#构建像素坐标点
camera_point=np.dot(rtmat,obj_point) #相机坐标系
c_point=np.dot(prjmat,camera_point)/Zc #图像物理坐标系
#由理想点生成畸变点
r2=c_point[:1,:]**2+c_point[1:2,:]**2
r2=np.repeat(r2,2,axis=0)
scale=1+k1*r2+k2*r2**2+k3*r2**3
c_point[:2,:]=c_point[:2,:]*scale
img_point=np.dot(kmat,c_point)#图像像素坐标系
#显示测试
corners=img_point[:2,:].T
#加入噪声,噪声范围-0.05-0.05
noise=(np.random.rand(corners.shape[0],corners.shape[1])-0.5)*0.1
corners+=noise
corners=np.expand_dims(corners,axis=1)
showimg = (np.ones((imgh, imgw, 3)) * 255).astype(np.uint8)
cv2.drawChessboardCorners(showimg, (col, row), corners, True)
if idx==0:
Testimg=showimg.copy()
#cv2.namedWindow('img',cv2.WINDOW_NORMAL)
cv2.imshow('img',showimg)
cv2.waitKey(500)
obj_points.append(each_obj_point)
img_points.append(corners)
#对虚拟生成的数据进行相机标定
use_init_k=True
if use_init_k:
ret, mtx, dist, rvecs, tvecs=cv2.calibrateCamera(obj_points,img_points,(imgw,imgh), kmat,None,
flags=cv2.CALIB_USE_INTRINSIC_GUESS|cv2.CALIB_ZERO_TANGENT_DIST)
else:
ret, mtx, dist, rvecs, tvecs=cv2.calibrateCamera(obj_points,img_points,(imgw,imgh), None,None)
if(ret):
print('K error: 1/dx:',mtx[0,0]-kmat[0,0],',1/dy:',mtx[1,1]-kmat[1,1])
print('D error: k1:', dist[0,0] - k1,
',k2:',dist[0,1] - k2,
',k3:', dist[0, 4] - k3
)
#undist = cv2.undistort(showimg, mtx, dist, None, mtx)
map1, map2 = cv2.initUndistortRectifyMap(mtx, dist, np.eye(3), mtx, (imgw,imgh), cv2.CV_32FC2)
undist = cv2.remap(Testimg, map1, map2,interpolation=cv2.INTER_LINEAR, borderMode=cv2.BORDER_CONSTANT)
result = np.concatenate((Testimg, undist), axis=1)
cv2.imshow("img", result)
cv2.waitKey(0)
生成的桶形畸变点看起来应该没啥问题

最终标定后,去除畸变的效果如下

对比的相机参数也差不多

不过是在传递了初始化相机内参数矩阵的情况下

如果不传,发现相机参数相差还是很大,这个可能是因为我标定点数据都是同一个平面导致的吧,后面有时间再研究.