前言

使用差分来解决算法题是十分常见的，对于优化算法有极大的作用

可以是原本O(n)的时间复杂度优化为O(1)，具体往下看

一、差分的作用

作用：

通过 差分数组

对原数组在区间[ l , r ]内进行加或减去数的操作由O(n) 的时间复杂度，优化为O(1)的时间复杂度

差分数组的主要适用场景是频繁对原始数组的某个区间的元素进行增减

二、介绍

给定原整数数组 a：a1,a2,a3…an

构造差分数组：原数组是b数组的前缀和数组

a1 = b1
a2 = b1 + b2 = a1 + b2
a3 = b1 + b2 + b3 = a2 + b3
......
an = an-1 + bn
bn = an - an-1【--构造函数】

如果我们需要对原数组在区间[ l , r ]内进行 加c 操作

则可以对 b 数组 的

b[l] += c , b[r + 1] -= c

操作

原理很简单，回想 b 数组反推 a 数组的过程，b[i] += 3 意味着给 a[i..] 所有的元素都加了 3，
然后 b[j+1] -= 3 又意味着对于 a[j+1..] 所有元素再减 3，
那综合起来，是不是就是对 a[i..j] 中的所有元素都加 3 了？

只要花费 O(1) 的时间修改 b 数组，就相当于给 a 的整个区间做了修改。
多次修改 b，然后通过 b 数组反推，即可得到 a 修改后的结果。

建议画图理解

变换：====>

其实，这里我们可以不关心 b 是怎么来的，因为 a 可以是 b的序列在[ i , i ]区间里面加上a[i]

b的初始可以是0

例如上方图片 ai = ai-1 + bi

==

b[i] += b[i – 1]

所以我们只关心并且注重：

b[l] += c , b[r + 1] -= c

最后求得的b[i] 就是原数组

三、例题

797. 差分 – AcWing题库

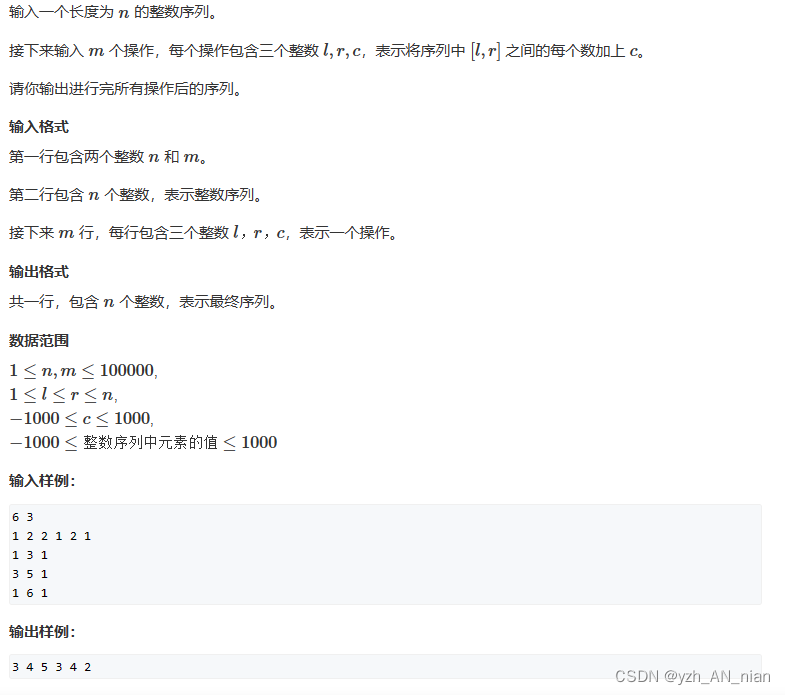
代码：

import java.util.*;
public class Main {
    static int[] a;
    static int[] b;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int nn = scanner.nextInt();// 长度nn
        int mm = scanner.nextInt();// mm个操作
        a = new int[100010];// 定义原数组序列
        b = new int[100010];// 定义差分数组
        for (int i = 1; i <= nn; i++) {
            numbers[i] = scanner.nextInt();// 写入数据，构建原数组
            insert(i,i,numbers[i]);
        }
        for (int i = 0; i < mm; i++) {
            int l = scanner.nextInt();
            int r = scanner.nextInt();
            int c = scanner.nextInt();
            insert(l,r,c);
        }
        for (int i = 1; i <= nn; i++) {
            b[i] += b[i - 1];
            System.out.print(b[i] + " ");
        }
    }
    public static void insert(int l,int r,int c){
        b[l] += c;
        b[r + 1] -= c;
    }
}

当然还有其他的写法

import java.util.*;
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int nn = scanner.nextInt();// 长度nn
        int mm = scanner.nextInt();// mm个操作
        int[] numbers = new int[100010];// 定义原数组序列
        int[] diff = new int[100010];// 定义差分数组
        for (int i = 1; i <= nn; i++) {
            numbers[i] = scanner.nextInt();// 写入数据，构建原数组
            diff[i] = numbers[i] - numbers[i - 1];// 构建差分数组
        }
        for (int i = 0; i < mm; i++) {
            int l = scanner.nextInt();
            int r = scanner.nextInt();
            int c = scanner.nextInt();
            diff[l] += c;
            diff[r + 1] -= c;
        }
        for (int i = 1; i <= nn; i++) {
            numbers[i] = numbers[i - 1] + diff[i];
            System.out.print(numbers[i] + " ");
        }
    }
}

二维差分

798. 差分矩阵 – AcWing题库

import java.util.Scanner;
public class DifferenceMatrix {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();// n行
        int m = scanner.nextInt();// m列
        int q = scanner.nextInt();// q个操作
        int[][] numbers = new int[1010][1010];// 数组序列
        int[][] diff = new int[1010][1010];// 差分数组
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                numbers[i][j] = scanner.nextInt();
                insert(i, j, i, j, numbers[i][j],diff);
            }
        }
        while (q -- != 0){
            int x1 = scanner.nextInt();
            int y1 = scanner.nextInt();
            int x2 = scanner.nextInt();
            int y2 = scanner.nextInt();
            int c = scanner.nextInt();
            insert(x1,y1,x2,y2,c,diff);
        }
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                numbers[i][j] = numbers[i - 1][j] + numbers[i][j - 1] - numbers[i - 1][j - 1] + diff[i][j];
                System.out.print(numbers[i][j]);
            }
            System.out.println();
        }
    }
    public static void insert(int x1, int y1, int x2, int y2, int c,int[][] diff){
        diff[x1][y1] += c;
        diff[x2 + 1][y1] -= c;
        diff[x1][y2 + 1] -= c;
        diff[x2 + 1][y2 + 1] += c;
    }
}

这位博主的总结是详细版：


详谈前缀和与差分

总结

以上就是今天要讲的内容，本文仅仅简单介绍了差分的使用，如有不足或错误希望大家可以提出，我一定改进！一起学习一起进步！