|q| < 1 证明:
lim
n
q
n
=
0
\lim_n{q^n} = 0
lim
n
q
n
=
0
,

通过利用二项式,放缩来进行证明或者两边同时取对数。


lim
n
→
inf
n
n
=
1
\lim_n\to\inf{ \sqrt[n]{n} = 1}
lim
n
→
in
f
n
n
=
1
证明成立
算术-几何不等式
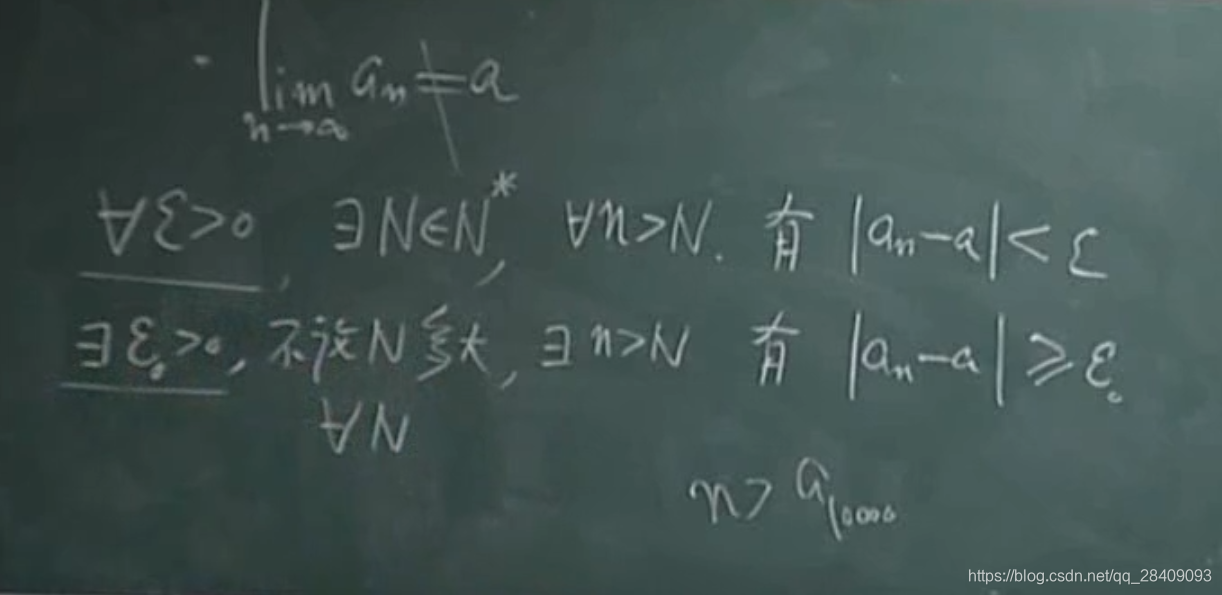
对于收敛的数列,换掉有限项对数列是否收敛没有关系,即不产生影响,因为我们考虑的是n>N后面无限的项。
如果一个数列有极限,那么这个数列是收敛数列
如果一个数列没有极限,那么这个数列是发散数列
收敛数列的性质
首先一个问题是一个数列如果存在极限,那么这个极限是否唯一?
假设有两个极限通过设
ϵ
\epsilon
ϵ
= (a + b )/ 2,证明这个不能成立,那么就可以证明唯一性。
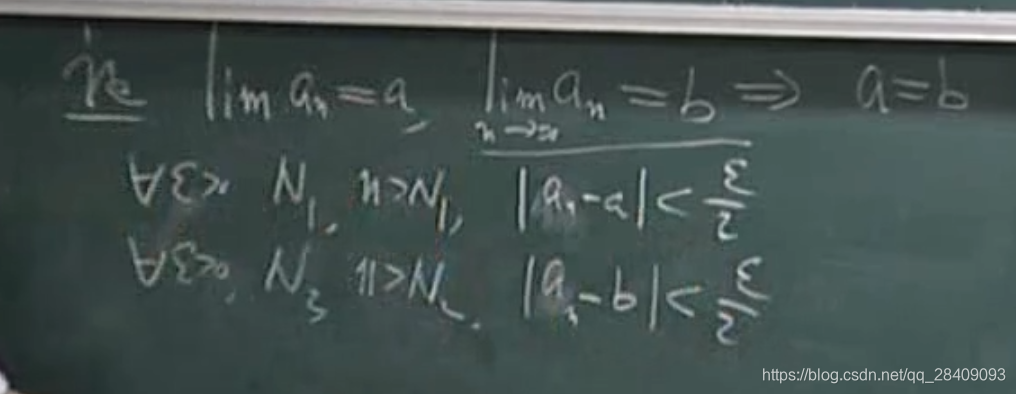
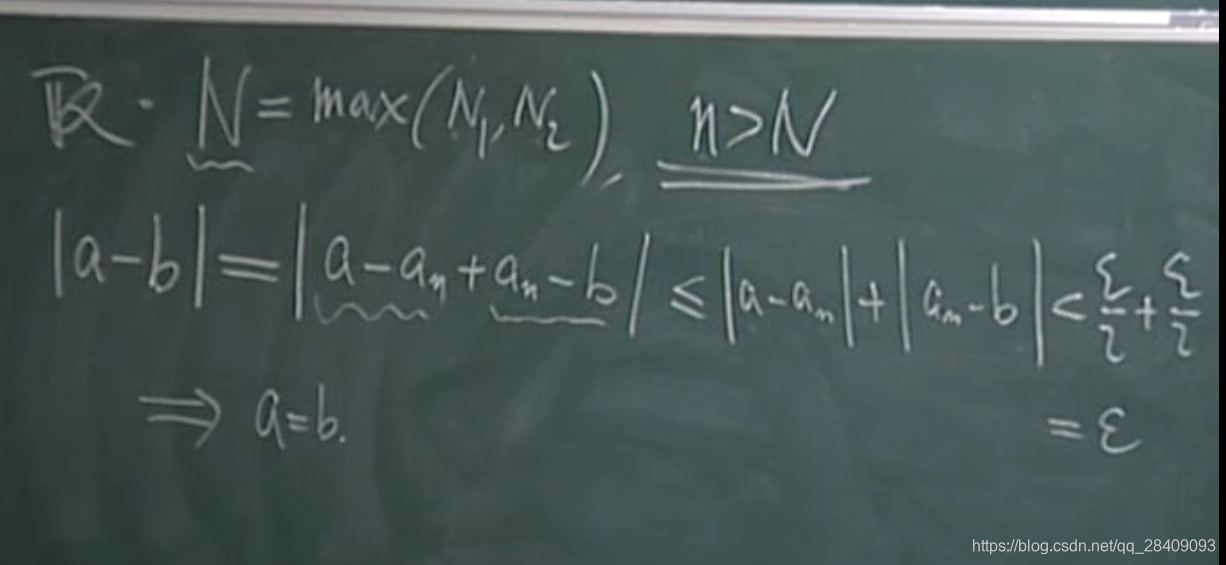
由于a,b是固定的数,由于任何两个不同的固定的数都不能做到差小于任意精度,所以a,b必然相等。因此极限只有一个。
tips:三角形不等式

一个数列向右走走到B就不能走了,向左走,走刀A就不能走了,说这个数列是有上界和下界的,即有界的。|
a
n
≦
M
a_n \leqq M
a
n
≦
M
|;
思想:想问题先从几何上想,再用数学语言表达出来
ji’x

数学语言:

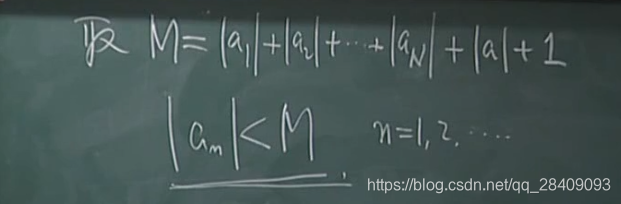
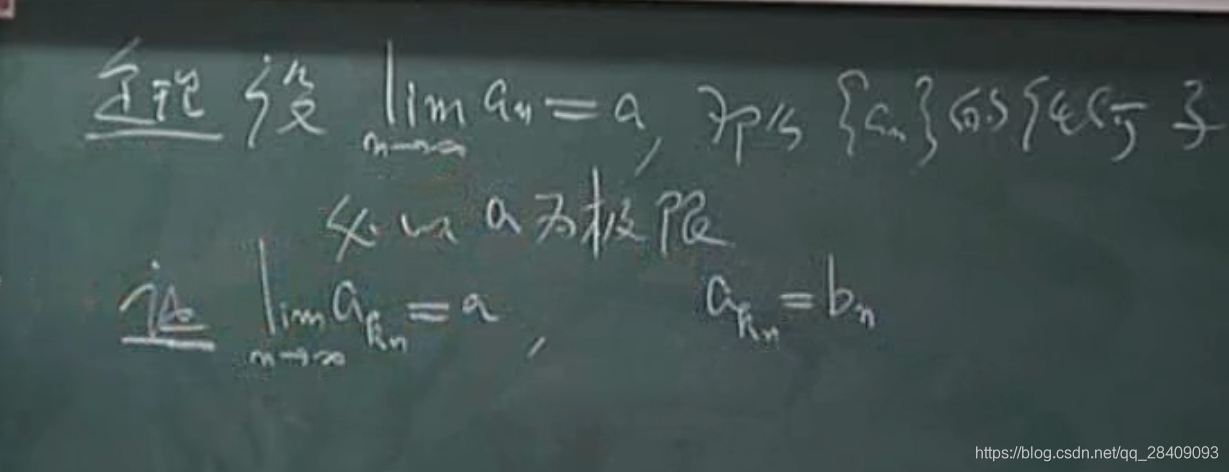
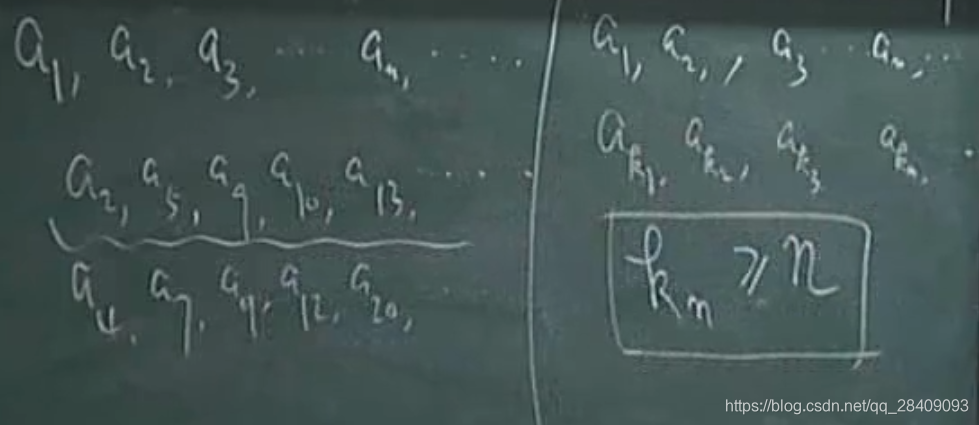
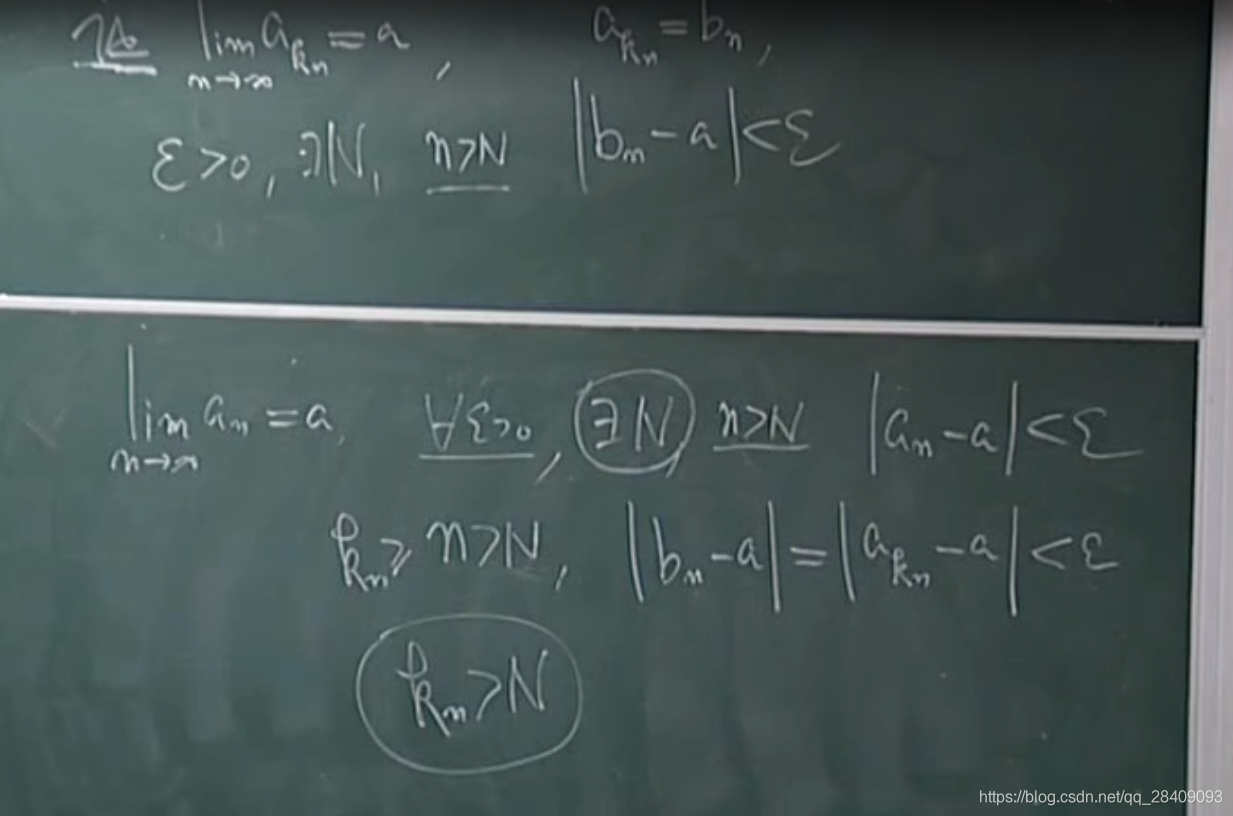
1、有界
2、子数列也是有极限的
3、极限唯一性。