协同过滤进化——矩阵分解
MF
一、针对问题
1、协同过滤处理稀疏矩阵能力较弱
稀疏矩阵在矩阵中,若数值为0的元素数目远远多于非0元素的数目,并且非0元素分布没有规律时,则称该矩阵为稀疏矩阵
2、协同过滤中,相似度矩阵维护难度大
无论是m个用户还是n个物品,构建相似度矩阵时,维数都很大
二、解决思路
引例:

运用隐向量,给每个用户与每首音乐打上标签
实际运用:
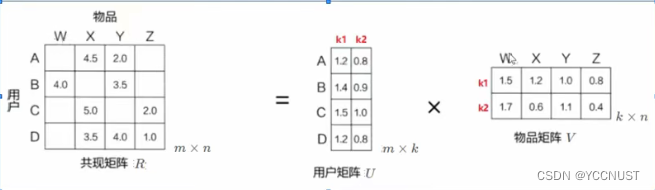
1、矩阵是稀疏的
2、隐含特征不可解释,即我们不知道具体含义,要模型自己学
3、K的大小决定隐向量表达能力的强弱,K越大,表达信息越强,理解起来就是把用户的兴趣和物品的分类划分的越具体
4、数学公式表达
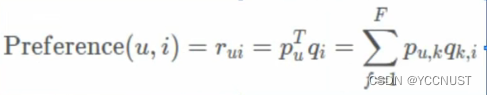
三、MF的几种方式
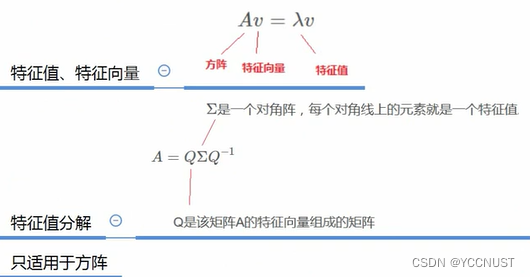
1、特征值分解
只适用于方阵,实际应用受限,淘汰掉了
2、奇异值分解(SVD)
定义:
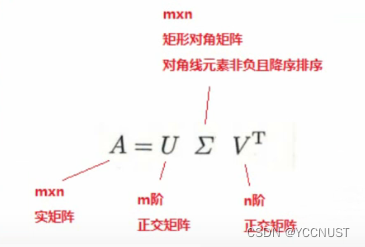
示例:

计算步骤:
1、
构造实对称矩阵
:
W
=
A
T
A
W=A^{T}A
W
=
A
T
A
2、
计算
W
W
W
的特征值和特征向量

3、
求得n阶正交矩阵
V
V
V

4、
求得mxn对角矩阵
∑
\sum
∑

5、
求得m阶正交矩阵
U
U
U
(利用上述已求变量)
①求
U
1
U1
U
1
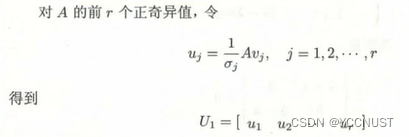
②
求
U
2
U2
U
2

③
得到最终
U
=
[
U
1
,
U
2
]
U=[U1,U2]
U
=
[
U
1
,
U
2
]
实例:


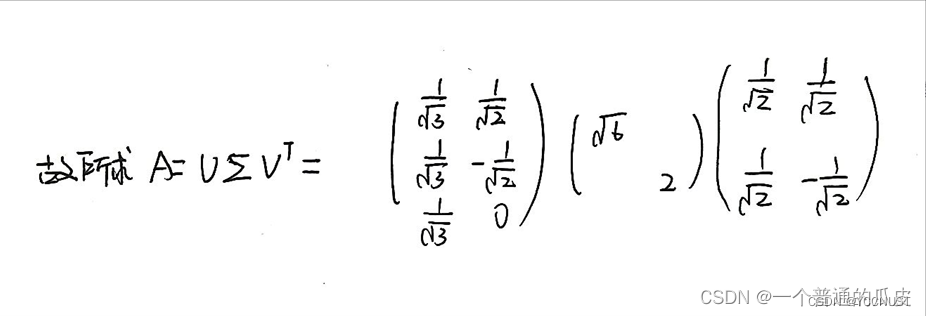
缺点:
1、传统的SVD分解,会要求原始矩阵是稠密的,而我们矩阵一般是稀疏的,则必须要对缺失元素填充,而一旦补全,时间复杂度会变高,且补全的元素不一定对
2、计算复杂度高,基本无法使用
3、Basic SVD(应用广)
将矩阵分解问题转化为【最优化问题】,通过
梯度下降优化
矩阵分解后的
预测函数:
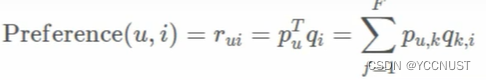
损失函数:
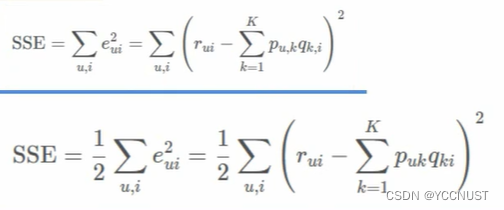
优化目标
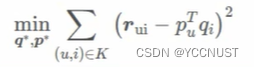
梯度下降求梯度:
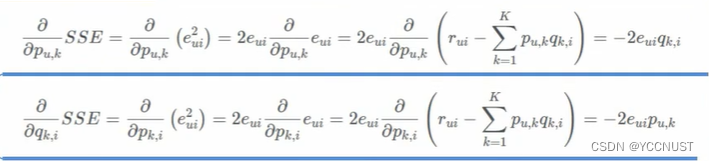
梯度更新
这里梯度更新用的第二种损失函数,2已约去
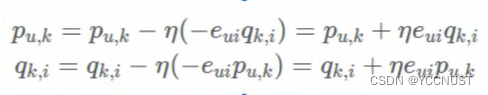
代码
import numpy as np
import math
import matplotlib.pyplot as plt
def Martix_decomposition(R,P,Q,N,M,K,alpha=0.0002, beta=0.02):
Q=Q.T
loss_list=[]
for step in range(5000):
for i in range(N):
for j in range(M):
if R[i][j] !=0:
error = R[i][j]
for k in range(K):
error-= P[i][k] * Q[k][j]
for k in range(K):
P[i][k]=P[i][k]+alpha*(2*error*Q[k][j]-beta*P[i][k])
Q[k][j]=Q[k][j]+alpha*(2*error*P[i][k]-beta*Q[k][j])
loss = 0.0
# 计算每一次迭代后的 loss 大小,就是原来 R 矩阵里面每个非缺失值跟预测值的平方损失
for i in range(N):
for j in range(M):
if R[i][j] != 0:
data=0
for k in range(K):
data=data+P[i][k] * Q[k][j]
loss=loss + math.pow(R[i][j] - data, 2)
# 得到完整loss值
for k in range(K):
loss=loss+beta/2* (P[i][k] * P[i][k] + Q[k][j] * Q[k][j])
loss_list.append(loss)
plt.scatter(step, loss)
if (step + 1) % 1000 == 0:
print("loss={:}".format(loss))
# 判断
if loss < 0.001:
print(loss)
break
plt.show()
return P, Q
if __name__ == "__main__":
N=5
M=4
K=5
R=np.array([[5,3,0,1],
[4,0,0,1],
[1,1,0,5],
[1,0,0,4],
[0,1,5,4]])
print("初始评分矩阵")
print(R)
#定义P,Q矩阵
P=np.random.rand(N,K)
Q=np.random.rand(M,K)
print("开始矩阵分解")
P,Q=Martix_decomposition(R,P,Q,N,M,K)
print("矩阵分解结束")
print(np.dot(P, Q))
#结果
初始评分矩阵
[[5 3 0 1]
[4 0 0 1]
[1 1 0 5]
[1 0 0 4]
[0 1 5 4]]
开始矩阵分解
loss=7.789967374611276
loss=1.5254249001655658
loss=1.2298493206088095
loss=1.1939728272813064
loss=1.1867845018472227
矩阵分解结束
[[4.98264887 2.97123772 3.65967064 1.00390809]
[3.97816195 2.38891837 3.23075132 1.00228606]
[1.01089469 0.97615413 2.77117286 4.97176877]
[0.99427186 0.84281943 2.32871786 3.98388103]
[3.06565871 1.02569453 4.98163023 3.98464188]]
进程已结束,退出代码0
4、RSVD
在Basic SVD目标函数的基础上,加入正则化参数(加入惩罚项),以防止过拟合
预测函数不变:
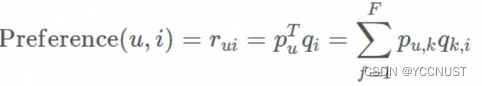
目标函数:
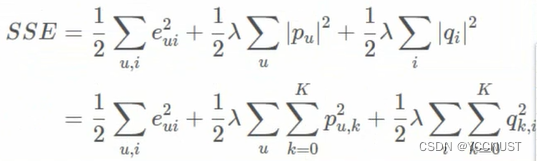
求梯度:
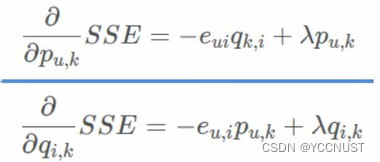
梯度更新:
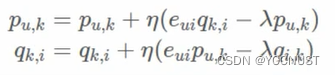
改进方向:
Netfix Prize提出了另一种LFM,在原来基础上加上偏置项,来消除用户和物品打分的偏差
原因:

预测函数:

目标函数:
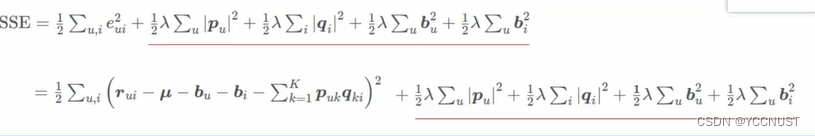
求梯度:
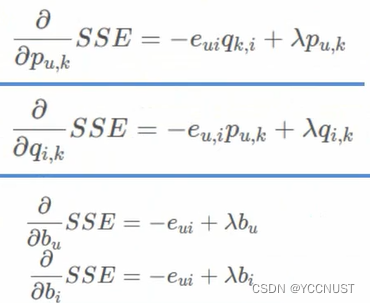
梯度更新:
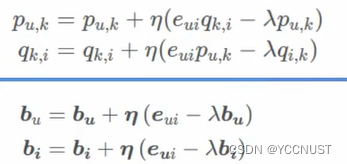
5、SVD++
引入用户评分过的历史物品。
物品之间的某种关联,会影响物品的评分
将这种关联对评分结果产生的影响,交给模型去学习
预测函数
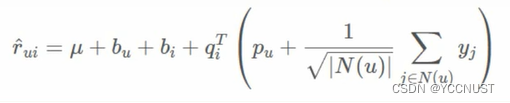
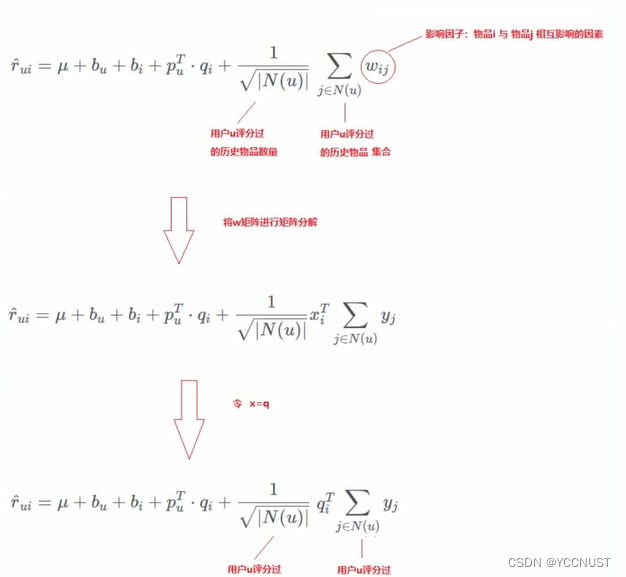
图示:要求User3对Item3的打分

四、MF优点与局限性

