目录
4.2.1 信号检测:检查由无数个相互正交信号叠加后的时域信号中是否有某一特定的信号。
步骤4:获取时域信号中复指数谐波分量的幅度An.x与An.y
1. 傅里叶分析方法的理论基础
在《深入理解信号的时域与频域,需要从熟悉的声音信号入手》中,得到了这样一个
定性
的结论:
任何时域的信号,都可以表示为不同频率的复指数信号(正弦信号)的无限叠加!
包括:连续周期信号、离散周期信号、连续非周期信号、离散非周期信号。
那现在的关键问题是:
(1)如何通过量化的分析时域信号到达有哪些频率分量信号组成?每个频率分量信号的幅度是多少?信号的相位多大?
(2)每个组成的基本频率分量信号为什么不是普通的正弦波信号?而必须是复指数正弦波信号?
这就需要求助于傅里叶分析工具!!!
2 傅里叶分析方法概述与基本框架
2.1 信号的频谱与频谱分析
(1)频谱:频率+幅度
信号的
频谱
是信号
内在
的成分组成。频域频谱是组成的频率分量f为自变量,幅度或强度为因变量的可视化的图形展示。有时候也称为频率信号。

信号的
频谱
是信号表示的一种新的表示方法,从频谱可以看到:
-
这个时域信号内部由哪些频率的
谐波分量
(正弦分量)组成; - 各个谐波分量的幅度;
- 各个谐波分量的初始相位;
幅度和相位的相对大小就反映了各谐波分量对时域信号贡献的大小或所占比重的大小。
(2)相位谱:频率+相位
反应各个谐波分量的初始相位的大小。
我们知道,正弦信号,即使频率相同、幅度相同,但初始相位不同,则信号叠加出来的效果是不一样的,最极端的案例是相差为0和相差为180度。
相差为0:为同向,信号的幅度是完全累计的。

相差180°:为反向,信号的幅度是完全抵消的。
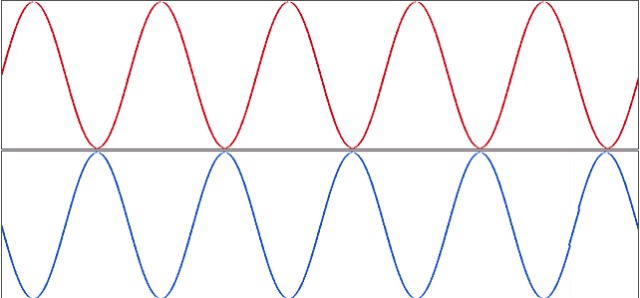
这反应谐波分量的相位对时域信号的影响。
(3)频谱分析:
频谱分析即是分析和呈现时域信号内部频谱的工具和方法。
-
图形法
-
数学公式法:
傅里叶分析方法就是一种数学分析方法。
2.2 傅里叶分析方法的概述
(1)强大的时域和频域分析能力
不同时域信号内部的频率组成是不一样的,通过统一的傅里叶变换数学工具,可以分析
任何时域信号
的内部频率组成。
(2)强大的信号合成与分解能力
可以把任何时域信号
分解
成频域的不同频率的信号,也可以把频域的不同的频率的信号
合成
为任意的时域信号。

(3)精确的量化能力
傅里叶不仅仅能否分析时域信号内含多少频率分量F(t),还能够分析不同频率分量的幅度A(t)和相位P(t)。
频率分量、幅度分量、相位分量,可能是离散的,也可能是连续的!完全精确量化!
2.3 傅里叶分析方法的框架

在上图中
(1)信号输入1:时域信号,连续周期信号、离散周期信号、连续非周期信号、离散非周期信号。
(2)信号输入2:复指数的正弦信号:
![]()
,不同的输入信号,虽然谐波分量的频率的个数是不相同,但相位都为0,幅度都为1.
(3)系统运算:不同类型的输入信号,傅里叶运算的方法不同,与输入信号的类型一一对应:连续时间傅里叶级数FS、离散时间傅里叶级数DTFS、连续时间傅里叶变换FT、离散时间傅里叶变换DTFT。
(4)输出信号:不同谐波分量的线性相加,每个谐波分量包括:频率、幅度、相位。
傅里叶运算的本质就是精确的量化:
-
有多少个谐波分量?有哪些谐波分量?谐波分量的数量和数值取决于什么? =》
取决于时域信号的周期性(非周期信号的周期无穷大) -
每个谐波分量的幅度、相位是多少?通过什么方法和手段量化出每个谐波分量的幅度和相位? =》
取决于谐波分量复指数信号与时域信号的卷积。

3 函数/信号的积分
3.1 函数/信号的积分
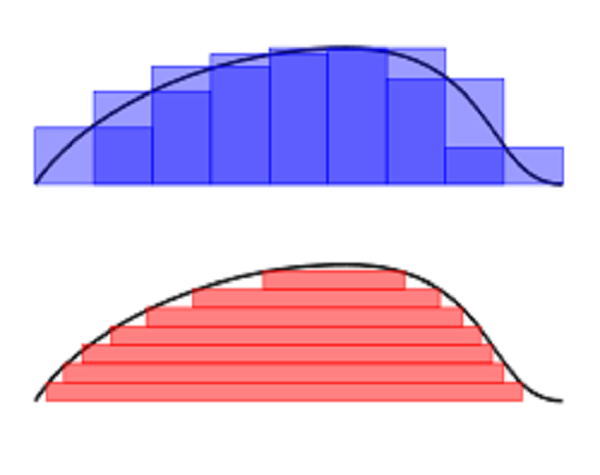
函数的积分:直观地说,对于一个给定的正实值函数,在一个实数
区间
上的定积分, 可以理解为在坐标平面上,由曲线、直线以及轴围成的
曲边梯形
的面积值(一种确定的
实数
值)。
3.2
函数/信号积分为0的物理意义
在
线性叠加
的
复合
信号中,如果某一分量信号/函数,在某一个积分区间积分为0,表明某个信号分量,无论在积分区间的波形如何变化,其对最终叠加后的
复合信号
的平均幅度(积分)影响为0,即没有任何影响!
例如:
y(t) = f1(t) + f2(t) =》 y(t) 是两个信号f1(t)和f2(t) 的叠加。
如果f2(t)的积分为0,即ʃf2(x)=0,则ʃy = ʃ (f1(t) + f2(t) = ʃ f1(t)
也就是说,虽然最终信号y(t) 瞬间幅度与 f2(t)有关,是f1(t)和f2(t) 的叠加,
但信号y(t) 在某个积分区间的平均幅度(积分幅度),实际上与 f2(t)无关,只取决于f1(t)!!!, f2(t) 对叠加后信号的平均幅度影响为0.
这个结论非常中重要!!!
这是正交函数调制互不影响、能够正确解调的理论基础!
4 函数/信号之间的相关性与正交
4.1 函数之间正交性的定义
两个函数/信号的相关性:是通过两个函数相乘以后的积分值来描述的。
(1)如果函数与自身相乘,在指定区间上的积分不为0。
(2)如果连个函数相乘之后的函数,在某个区间的积分值为0,则这两个函数是不相关的,即正交的。

一组函数的性质可以类比矢量的正交,“两个函数相乘再积分” 这个步骤可以类比无数个矢量(在函数区间的采样值)的内积。
如果两个不同的矢量正交(垂直),则它们的内积为零.如果它们的模长不为零,则一个矢量与自身内积不为零。
如果给正交函数系中的每个函数的平方进行归一化,则得到:

这里有几个
关键点:
(1)两个函数的相乘
(2)对两个函数相乘的结果函数进行
积分
(3)积分的值为0
4.2 两个函数正交的本质、意义与作用
4.2.1 信号检测:
检查由无数个相互正交信号叠加后的时域信号中是否有某一特定的信号。
假设1:
一个时域信号是有无数个相互正交的时域信号叠加而成的,例如:
f1(t)、f2(t) 、f3(t) 、f4(t)……fn(t)为两两正交的函数/信号. n = 1,2,3,4,5,。。。。则任意两个不同的函数相乘后的积分为0.
时域信号f(t) = f1(t) + f2(t) + f4(t) + f5(t);
目标1:检查线性叠加后的时域信号f(t)中是否内含f3(t)的信号?
检测方法:用
f3
(t)与f(t) 相乘后再积分
//正交函数相乘后的积分为0
判定结果:g(t)为0,f(t)不含有f3(t)信号。
f(t) = f1(t) + f2(t) + f4(t) + f5(t) = A1cos(ωt) + A2cos(2ωt) + A3cos(3ωt) + A4cos(4ωt),
目标2:检查线性叠加后的时域信号f(t)中是否内含f2(t)的信号?
检测方法1:用
f2
(t)与f(t) 相乘后再积分
判定结果:g(t)不为0,f(t)
含有
f2(t)信号。
f(t) = f1(t) +
f2(t)
+ f4(t) + f5(t) = A1cos(ωt) + A2cos(2ωt) + A3cos(3ωt) + A4cos(4ωt),
4.2.2 特征提取:提取检测到的信号的特征
假设2:
一个时域信号是有无数个相互正交的时域信号叠加而成的,如:
- 假设1:f1(t)、f2(t) 、f3(t) 、f4(t)……fn(t)为两两正交的函数/信号. n = 1,2,3,4,5,。。。。则任意两个不同的函数相乘后的积分为0.
- 假设2:f1(t) = A1cos(ωt); f2(t)=A2cos(2ωt); f3(t)=A3cos(3ωt); f4(t)=A3cos(4ωt);fn(t)=A3cos(nωt);
- 假设3:时域信号f(t) = f1(t) + f2(t) + f4(t) + f5(t) = A1cos(ωt) + A2cos(2ωt) + A3cos(3ωt) + A4cos(4ωt),
- 假设4:时域波形:
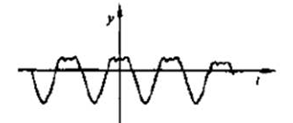
目标:
提取出f2(t)信号的特性,这里是指正弦波的幅度A1.
检测信号
:cos(2ωt), ω为已知频率。
方法:积分
这样,通过检测信号cos(2ωt),就可以检测出时域信号f(t)中包含cos(2ωt),以及其幅度A2的值。
傅里叶分析正是基于上述正交函数线性叠加后两个重要的特征:函数/信号的检查与特征提取。
现在的关键和首要问题是:如何给傅里叶分析指定组成时域信号的基本的频域信号,即正交函数!
5. 基本正交信号的选择
5.1 正弦、余弦信号的正交性
在无线通信中,通常使用sin和cos作为最基本的信号,
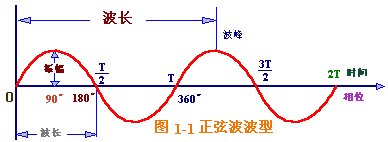
决定正弦信号sinx的参数有:频率f、A幅度和初始相位θ0,作为基本信号,令其初始相位θ0=0,幅度A=1,得到sin(ωt) = sin(2πf)。周期T=1/f
余弦函数cosx是与正弦信号sinx初始相位相差90°,即π/2,因此也统称为正弦信号。
因此正交信号的关键参数就剩下了频率。假设基准频率为ω1,这样就可以派生出一组频率:1ω1、2ω1、3ω1、4ω1…….,这样就无数个sin和cos函数

上述函数是完备正交函数集,所谓完备正交函数集,是指任意两个不用频率的信号或同频的sin与cos信号都是两两正交的,即相乘后的积分为0.
5.2 基本复指数信号的正交性
在傅里叶分析中,选择的不是单路的sin(nωt),也不是单路的cos(nωt) ; n=1,2,3,4…….
而是选择的是sin(nωt)+i*cos(nωt)的复指数信号
集,包含一系列正交的复指数信号。

上述的复指数信号
(1)同频的复指数信号的是实部与虚部是正交的。
(2)不同频的复指数信号之间是正交的。
数学表达公式如下:

5.3 为什么选择复指数信号作为基本信号?
我们知道,复指数信号,在x轴方向的投影为sinx,在y轴方向的投影为cosx。
为什么不直接选择单路的sinx或单路的cosx信号集呢?这不更简单吗?
而要选择同频率的两路信号的复指数信号作为基本信号集呢?这不是舍近求远?舍弃简单选择复杂化吗?
其实这里是有原因的:
(1)求正弦信号的2个参数:幅度和相位,需要构建2个方程。
在分析正交信号的特征提取案例中,只涉及到了一个正弦信号的参数,即幅度A,但实际中,确定一个正弦信号除了幅度外,还有初始相位。
因此一个方程是无法同时确定幅度和相位的。如
4.2.2章节案例中,只能获得幅度这个特征值。因此需要两路信号,两个方程,就可以获取两个参数。
(2)通过幅度参数,获取相位参数。

如上图所示,计算正弦信号幅度和相位有两种方法:
第一种方法:直接获取复信号的幅度r和初始相位θ:
r * sin(nωt+θ0)
第二种方法:先获取复信号在x轴和y轴方向的投影的幅度a和b。通过a和b的计算,就可以得到复信号的幅度r和初始相位θ。
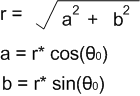
傅里叶分析采用了后一种方法来确定时域信号中内含的复信号的
幅度和相位
:
a*sin(nωt)+i*b*cos(nωt)
上述两种方法是等价的,但后一种方法是通过计算幅度来计算相位,充分利用复指数数学计算的优点,避免了大量三角函数的计算。
接来下我们看看,傅里叶是如何量化,时域信号中的频域复指数信号,在x轴和y轴上投影信号cosx和sinx对应的幅度值a和b的。
6. 傅里叶分析的基本思路
6.1 时域信号的类型与傅里叶分析的类型
不同类型的时域信号,会影响复指数信号序列的形式与信号的参数。
在傅里叶变换中,把时域信号分为如下几种类型以及对应的傅里叶变换。
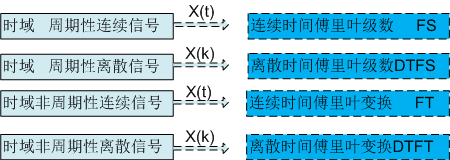
在上述四中类型的时域信号中,其中最简单的、最基础性的是:周期连续信号的傅里叶分析。
因此傅里叶分析由
周期连续信号开始,然后扩展的离散信号,在扩展到非周期信号。这是解读各种情形下傅里叶变换的基本思路。
(1)连续的、周期信号
![]()
时域上任意连续的、周期信号可以分解为
无限多个
、
离散的
、
非周期的
、
正交的
复指数信号之和,称之为傅里叶
级数
。
(2)非周线信号
非周期与周期是辨证统一的:
当周期当时域信号的周期为无穷大,即T=无穷,周期信号就转化为非周期信号。
周期无穷,就意味频率接近与0,那么非周期信号的基波频率接近于0,相邻两个谐波频率之间的间隔接近与0.
非周期信号就可以分解为
无限多个
、
连续的
、
正交的
复指数信号之和,称之为傅里叶
变换
。
所谓连续的复指数信号是指:
相邻
的两个复指数谐波信号的频率间隔接近为0.

(3)离散信号
连续信号与离散信号是辨证统一的,当离散信号的间隔变成无穷小,离散信号就转化为连续信号。
离散信号与连续信号的区别,就是用离散累加
和
替代
积分
。

6.2 傅里叶分析的量化目标

傅里叶分析无非是分别获取时域信号中直流信号的参数:幅度;正弦交流信号的参数:幅度、频率、相位。
(1)时域信号中直流分量的特性:直流分量的幅度A0;
相当于其中n=0
(2)时域信号中所有复指数信号基波分量的频率:正弦交流分量的频率
ω; 相当于其中n=1
(3)时域信号中所有复指数信号谐波分量的频率:正弦交流分量的频率
ωn =
n*ω; 其中n=2,3,4….
(4)时域信号中所有复指谐波信号在x轴投影信号cosx信号的幅度
An.x; 其中n=2,3,4….
(5)所有复指谐波信号在y轴投影信号sinx信号的幅度:
An.y; 其中n=2,3,4….
(
6
)
时域信号中所有复指谐波信号的幅度An;
其中n=2,3,4….
An是根据An.x和An.y间接获得的:
(7)时域信号中所有复指谐波信号的相位θn
θn
是根据An.x和An.y间接获得的:
An.x = An*cos(θn)
An.y = An * sin(θn)
最终获得:
An.x * cos(nωt) + i*An.y*sin(nωt)
= An *e^j(nωt)
= An * cos(nωt+θn) ;
6.3 傅里叶分析的参数量化模型
(1)基本量化模型
下图是通过傅里叶分析从时域信号中获取谐波分量的幅度特征的基本模型:
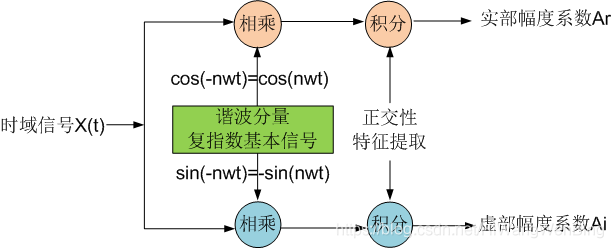
是不是似曾相识?是的,这个模型就是从高频已调信号中解调出基带信号的模型!!!
该模型是利用函数正交性原理,通过指定频率的复指数信号,从时域信号中获取指定频率的复指数信号的特征。
不同的类型的时域信号,提取复指数信号的谐波分量的实部和虚部系数的模型是相同的,只是计算公式略有差别而已!
最终会得到如下谐波信号序列:
An.x * cos(nωt) + i*An.y*sin(n*ωt) ;
{n=….-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6…….} ,
其中
n=0时, 谐波频率nωt=0,A0.y=0,A0.x就是直流信号的幅度,简称A0。
n=1时,谐波频率nωt=ωt,即基波频率

(2)An.x和An.y幅度可以为正或负

根据
An.x * cos(nωt) + i*An.y*sin(nωt),
如果只有正幅度,复指数信号只能是: cosx + i*sinx
如果幅度可正可负,这就意味着参与构建时域信号的谐波信号的
种类增加到4种。
+cosx + i*sinx
-cosx – i*sinx
+cosx + i*sinx
-cosx + i*sinx
负幅度的引入,把复信号的相位控制有【0,90°】,扩展到了【0,360°】或者说【-180°,180°】
(3)频率nω可正数,可负数

根据cos(-x) = cos(x); sin(-x) = – sinx.
对于cosx,负频率与正频率等价的。
对于sinx,负频率相当于正频率信号的幅度 * -1.
复频率的引入,把复信号的相位控制有【0,90°】,扩展到了【-90°,90°】
因此幅度的符号,已经包含了负频率的效果。
(4)那么为什么还需要负频率?
主要原因还是因为复指数的数学运算需要:
负频率的引入,把三角函数的运算空间可以转化为复指数运算空间,极大的简化了数学运算。
(5)负频率的物理意义
负频率的引入是解决复指数运算问题 ,但负频率并非没有物理意义。
-
复指数信号:
虚指数函数在三维空间中螺旋函数
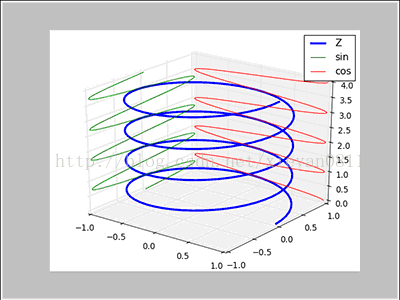
-
正频率:
逆时针旋转
如下是正频率的复指数信号中实部信号cos(x) 与sin(x)的关系图。

其物理意义是:
虚指数函数
逆时针旋转时
,在x轴方向的投影是余弦函数,
虚指数函数
逆时针旋转时,
在y轴方向的投影是正弦函数。
- 负频率:顺时针旋转
如下是负频率的复指数信号中实部信号cos(-x) 与sin(-x)的关系图。

其物理意义是:
虚指数函数
顺时针旋转时
,在x轴方向的投影是余弦函数,
虚指数函数
顺时针旋转时,
在y轴方向的投影是正弦函数。
7 傅里叶分析的9大步骤
步骤1:获取时域信号中
直流分量幅度A0
直流分量是谐波序号n=0的情形,也是谐波频率=0的情形。
此时提取的是时域信号中的直流分量的特性,即直流分量的幅度。
![]()
直流分量值只与时域信号在其周期内的积分相关,
直流分量值与时域信号包含多少复指数的正弦交流信号无关。
(1)A0是周期信号在整个信号周期积分的平均值。
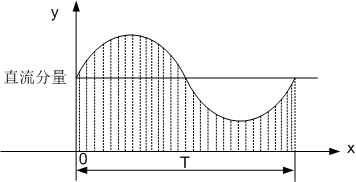
(2)如果周期信号在一个周期内的积分为0,则表明周期信号没有直流分量。
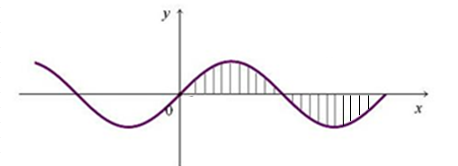
(3)
如果周期无穷大,就变成非周期信号,直流分量a0就是在整个时间区间内积分的平均值。

步骤2:获取时域信号中
复指数基波信号的频率
ω
基波分量是谐波序号n=1的情形。
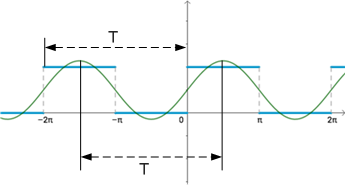
复指数信号(正弦信号)
基波分量(频率最小,周期最大的正弦信号)
的周期T等于时域信号的周期T。
时域信号
中基波分量的频率为:
ω=2πf = 2π/T。其中T为时域信号的周期。
-
周期时域信号的周期越大,频率越小,复指数集中基波信号的
频率
ω
越小。 -
周期时域信号的周期无穷大时,时域信号就变成了非周期信号,复指数集的基准频率
ω也就越接近于0。
步骤3: 获取时域信号中
复指数谐波分量的频率n*
ω
谐波分量是基波分量的n倍,一旦基波分量的频率ω确定了,那么谐波分量也就确定了, ωn =
n*ω, n=0,1,2,3,4……
-
时域信号的周期越大,频率越小,复指数集中基波信号的
频率
ω
越小。 -
时域信号的周期越大,频率越小,复指数集中
谐波分量n*ω之间的间隔(也等于ω)越小
,也就越密集。 -
时域信号的周期无穷大时,复指数集的基准频率
ω就越接近于0,
各个频率分量间隔也接近于0,复指数集也就接近频率连续信号集!
如下图所示:
步骤4:获取时域信号中
复指数谐波分量的幅度An.x与An.y
(1)解调模型

(2)数学公式推导


An.x:用余弦信号cos(n*ωt),与时域信号进行相乘,然后求积分,然后再除以时域信号的周期,根据前面提到的函数正交性原理,就可以获取时域信号中,cos(n*ωt)分量信号的幅度。
An.y:用余弦信号sin(n*ωt),与时域信号进行相乘,然后求积分,然后再除以时域信号的周期,根据前面提到的函数正交性原理,就可以获取时域信号中,sin(n*ωt)分量信号的幅度。
上面的运算是不是似曾相识? 是的!这就幅度调制解调的过程!!! 可以参考模拟和幅度幅度调制
上面的运算是不是似曾相识? 是的!这也是卷积运算的过程!!!cos(n*ωt)和sin(n*ωt)就是算子,是卷积核!!!
得到上述结果的前提是:假设时域信号中的谐波分量的函数都是正交的!
因此,时域信号中的复指数谐波分量的幅度,
取决于时域信号自身和复指数谐波分量的频率。
(3)关于时域非周期函数
上述的计算是基于时域周期函数获得的,实际上,随着周期的变大,周线函数逐渐丧失周期性,当周期无穷大时,周期信号变成非周期信号。
计算公式大体保持不变:
只需要做如下的修订:
- 设定T = 2π,即360°全周期。
- 积分周期为负无穷到正无穷
步骤5:获取时域信号中
复指数谐波分量的幅度An
An是根据An.x和An.y间接获得的:
步骤6:获取时域信号中
复指数谐波分量的相位
θn
θn
是根据An.x和An.y间接获得的:
An.x = An*cos(θn)
An.y = An * sin(θn)
步骤7:组合复指数信号
在获得复指数相应的参数后,就可以组合成不同格式的时域信号中复指数信号了
复指数形式:
复数形式:
三角形式:
步骤8:绘制时域信号的频谱图
根据上面步骤获得的所有谐波分量的频率和其对应的幅度,就可以画出时域信号的频谱图。
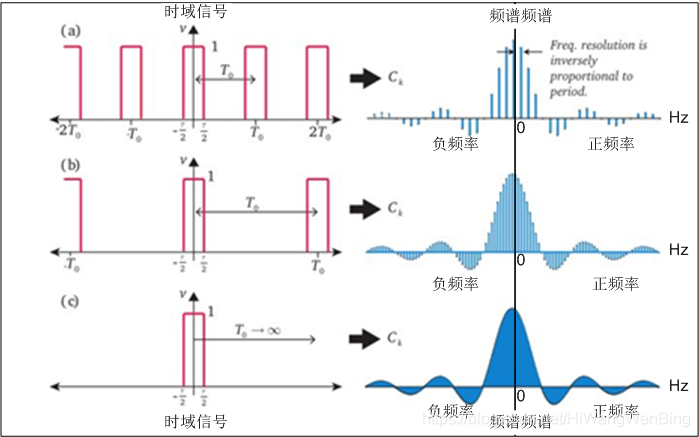
不同时域信号的频谱图是不一样的,这里以周期脉冲信号为例,如下图所示。
同时展示了周期信号演变非周期信号时,频谱图有离散向连续的转换。
时域信号的周期越小,频率最大,基波信号的频率越大,谐波信号的频率的间隔就越大,在频谱图上就越离散。
时域信号的周期越大,频率最小,基波信号的频率越小,谐波信号的频率的间隔就越小,在频谱图上就越密集,密集到无效小,就是连续频谱。

左边是时域信号,这里实例是周期脉冲信号。
右边是频域频谱,每个蓝色分量表示该频率信号的幅度。
正频率表示:逆时针旋转的频率分量
负频率表示:顺时钟旋转的频率分量
正负频率是对称的。
步骤9:绘制时域信号的相位谱图
相位谱图反应的是时域信号中,包含的每个谐波分量的初始相位以及其对应的正弦信号的幅度。
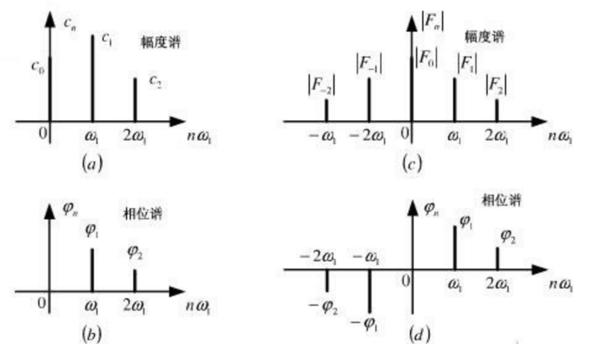
在实际应用中,相位谱图没有频谱图应用广泛。
在实际的PSK相位调制和QAM的正交幅度调制中,星座图本身就以及包含了相位信息,因此大多数情况下,没有必要再单独画一个相位谱图。
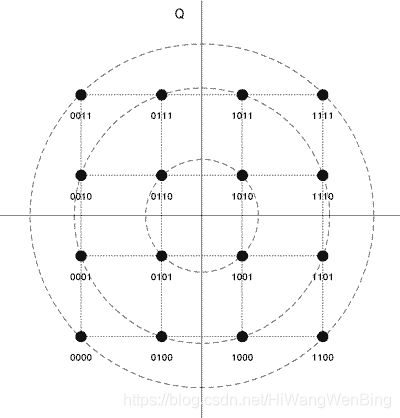
(1)PSK调制星座图:

(2)QAM调制星座图: