最短路径算法—狄杰斯特拉算法
一.介绍
这是一种按照路径长度递增的次序产生最短路径的算法,采用的是
贪心
的思想,对带权图(有向和无向均可)寻找最短路径;该算法对于不含
负权
的网来说,是目前已知的最快的
单源
最短路径算法,时间复杂度为o(n^2)
二.算法介绍与代码实现
首先我们看以这张图为例:
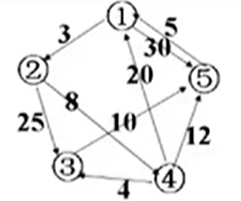
该图的领接矩阵表示为:

1.首先我们需要三个数组
(数组下标从1开始)
mark
:用来标记单源顶点(我们这里取为顶点1)到该顶点的最短路径是否已经求到了
dist
:标志单源顶点到该顶点的最短路径长度
path
:表示到该节点的前驱节点
2.三个数组初始化
mark: 1 0 0 0 0
dist: 0 3
∝
{\propto}
∝
∝
{\propto}
∝
30
path: 0 1 1 1 1
3.算法开始
狄杰斯特拉算法的核心思想是通过已有的最短路径以他为参照来优化到其他顶点的最短路径。
简单的概括过程就是每次从mark=0的顶点中去寻找dist最小的那个点那么这个点的最短路径就找到了,接下来从该顶点出发把剩下的mark=0的顶点的dist进行一遍优化(注意是优化,此时不一定是最短的路径),当然在上述过程中要注意对mark与path的更新,下面我们用上面的例子演示一下。
mark: 1 0 0 0 0
dist: 0 3
∝
{\propto}
∝
∝
{\propto}
∝
30
path: 0 1 1 1 1
找从mark=0最小的dist,即3,于是更新得到,mark[2]=1,path[2]就是1不用更新,然后用得到的新的最短路径去更新剩下的mark=0,那么有dist[3]=3+25<
∝
{\propto}
∝
,dist[4]=3+8<
∝
{\propto}
∝
,dist[5]仍然为30,因为3+
∝
{\propto}
∝
>30,同时更新path[3]=2,path[4]=2
此时:
mark: 1 1 0 0 0
dist: 0 3 28 11 30
path: 0 1 2 2 1
接下来按照上面的方式最后得到

4.代码实现
import org.junit.Test;
import java.util.Scanner;
public class Test1 {
int INFINITY = 65535;
int [][]Vertex={
{},
{0,0,3,INFINITY,INFINITY,30},
{0,INFINITY,0,25,8,INFINITY},
{0,INFINITY,INFINITY,0,INFINITY,10},
{0,20,INFINITY,4,0,12},
{0,5,INFINITY,INFINITY,INFINITY,0}
};//领接矩阵
int []mark={0,1,0,0,0,0};
int []path={0,0,1,1,1,1};
int []dist={0,0,3,INFINITY,INFINITY,30};
@Test
public void Test() {
Dijstra(5);
for(int i=1;i<=5;i++){
System.out.print(mark[i]+" ");
}
System.out.println();
for(int i=1;i<=5;i++){
System.out.print(dist[i]+" ");
}
System.out.println();
for(int i=1;i<=5;i++){
System.out.print(path[i]+" ");
}
}
//传入顶点数
void Dijstra(int n){
int marknum=n-1;//记录0的个数
int index;
while (marknum>=1)
{
index = Find(n);
mark[index]=1;//表示找到最短路径了
for(int i=1;i<=n;i++){
if(mark[i]==0&&Vertex[index][i]+dist[index]<dist[i])
{
dist[i]=Vertex[index][i]+dist[index];
path[i]=index;
}
}
marknum--;
}
}
//寻找mark为0的dist最小顶点
int Find(int n){
int index = 1;
while(mark[index]!=0)
index++;
int min = dist[index];
for(int i=index+1;i<=n;i++){
if(mark[i]==0&&dist[i]<min) {
index=i;
min=dist[i];
}
}
return index;
}
}
输出:
1 1 1 1 1
0 3 15 11 23
0 1 4 2 4
当然上面的图的信息都是直接保存在数组里面,我们也可以定义Graph类,在构造方法中完成初始化
//定义图类
class Graph{
int INFINITY = 65535;
int [][]Vertex;//领接矩阵
int []mark;
int []path;
int []dist;
String[] name;//记录每个节点的别名
Scanner scanner;
public Graph(){
//输入节点的个数
scanner = new Scanner(System.in);
System.out.println("请输入顶点的个数");
int n = scanner.nextInt();
System.out.println("请输入边的个数");
int numEdge = scanner.nextInt();
mark = new int[n+1];
mark[1]=1;
path = new int[n+1];
for(int i=1;i<=n;i++)
path[i]=1;
dist = new int[n+1];
Vertex = new int[n+1][n+1];
for(int i=0;i<n;i++)
for(int j=0;j<n;j++){
if(i!=j)
Vertex[i][j]=INFINITY;
}
for(int i=2;i<=n;i++)
dist[i]=Vertex[1][i];
name = new String[n+1];
System.out.println("请依次输入每个顶点的名字");
for(int i=1;i<=n;i++)
{
name[i]=scanner.next();
}
System.out.println("请依次输入每条边,输入方式为:顶点1编号 顶点2编号 权重");
int row,col,weight;
for(int i=1;i<=numEdge;i++){
row = scanner.nextInt();
col = scanner.nextInt();
weight = scanner.nextInt();
Vertex[row][col]=weight;
}
scanner.close();
}
//打印领接矩阵
public void printVertex(){
for (int[] vertex : Vertex) {
for (int i : vertex) {
System.out.print(i+" ");
}
System.out.println();
}
}
//传入顶点数
void Dijstra(int n){
int marknum=n-1;//记录0的个数
int index;
while (marknum>=1)
{
index = Find(n);
mark[index]=1;//表示找到最短路径了
for(int i=1;i<=n;i++){
if(mark[i]==0&&Vertex[index][i]+dist[index]<dist[i])
{
dist[i]=Vertex[index][i]+dist[index];
path[i]=index;
}
}
marknum--;
}
}
//寻找mark为0的dist最小顶点
int Find(int n){
int index = 1;
while(mark[index]!=0)
index++;
int min = dist[index];
for(int i=index+1;i<=n;i++){
if(mark[i]==0&&dist[i]<min) {
index=i;
min=dist[i];
}
}
return index;
}
}